미분

微分, Differentiation쌀가루(米粉), 적분 거꾸로

개요

미분이란 어떤 함수로부터 도함수(derivative)를 얻는 것을 말한다.

즉 미분(differentiate)하면 미분(differential)이 나오는 게 아니고 도함수가 나온다. 뭔 당연한 소리를 그렇게 강조하냐고 생각할 수 있는데, [math]\displaystyle{ f(x) }[/math]를 미분하면 나오는 게 뭐냐고 했을 때 보통 ‘미분’이라거나 딴소리를 하지 ‘도함수’라고 이름을 제대로 불러 주는 사람은 생각보다 적다.

도함수란 각 점에 대해 그 점에서의 미분계수(differential coefficient)를 대응시키는 함수를 말하고, 미분계수는 거칠게 말하면 그 점에서의 기울기 즉 순간변화율이다.

역사

미분법은 곡선에 접선을 그리는 문제와 함수의 극댓값, 극솟값을 구하는 문제를 연구하는 데서 비롯되었다는 것이 정설이다. 17세기에 케플러는 함수가 극댓값이나 극솟값을 갖는 점의 근방에서는 함수의 증분이 거의 0에 가깝다는 점을 지적했다. 데카르트와 페르마는 해석기하를 고안하여 곡선의 접선을 구하는 방법, 함수의 극대, 극소를 찾는 방법에 대한 연구를 본격적으로 하기 시작했다. 특히 페르마는 케플러의 아이디어를 극댓값과 극솟값을 결정하는 방법으로 변형했다. 그의 방법은 함수 [math]\displaystyle{ f(x) }[/math]에 대하여 [math]\displaystyle{ \frac{f(x+h)-f(x)}{h} }[/math]를 계산한 다음 [math]\displaystyle{ h=0 }[/math]일 때 이식의 값이 0이 되는 점을 찾는 것과 같다. 페르마의 방법은 완벽하지 못했지만 결국 [math]\displaystyle{ f'(x)=0 }[/math]을 만족시키는 x의 값을 찾는 것이므로 오늘날에는 '페르마의 정리' 혹은 '내부 극값 정리(Interior extremum theorem)'라고 부른다.

'수 [math]\displaystyle{ f(x) }[/math]가 [math]\displaystyle{ x=a }[/math]를 포함하는 구간에서 미분가능하고 [math]\displaystyle{ x=a }[/math]에서 극값을 가지면 [math]\displaystyle{ f'(a)=0 }[/math]이다.

그러나 페르마의 방법에서 [math]\displaystyle{ f'(a)=0 }[/math]은 함수 [math]\displaystyle{ f(x) }[/math]가 [math]\displaystyle{ x=a }[/math]에서 극값을 가질 충분조건은 아니며, 또한 [math]\displaystyle{ f'(a)=0 }[/math]이고 [math]\displaystyle{ x=a }[/math]에서 극값을 갖는다고 하더라도 그 값이 극댓값인지 극솟값인지를 판단할 수는 없다.

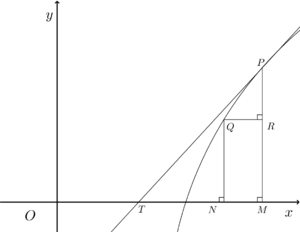
뉴턴 이전에 미분법에 관한 가장 현대적인 접근 방법을 보인 사람은 뉴턴의 스승이고 뉴턴에게 자신의 교수직을 물려준 것으로 유명한 배로이다. 배로는 그의 저서 '광학과 기하학 강의'에서 미소 삼각형을 이용한 접선을 찾는 방법을 보였는데, 오른쪽 그림에서 곡선 위의 점 Q가 점 P에 가까워지면 점 P에서 곡선에 그은 접선의 기울기 [math]\displaystyle{ \frac{\overline{PM}}{\overline{TM}} }[/math]은 [math]\displaystyle{ \frac{\overline{PR}}{\overline{QR}} }[/math]에 가까워짐을 이용하여 접선을 구했다.
배로는 자신의 방법으로 많은 곡선들의 접선을 구하는 데 성공했다. 그는 또한 미분법과 적분법이 역연산임을 알아낸 최초의 수학자로 알려져 있는데, 이 중요한 정리가 '미적분의 기본 정리'로 '광학과 기하학 강의'에 수록되어 있다.

미분계수

함수 [math]\displaystyle{ y=f(x) }[/math]에 대하여 [math]\displaystyle{ x }[/math]의 값이 [math]\displaystyle{ a }[/math]에서 [math]\displaystyle{ b }[/math]까지 변할 때, 함숫값은 [math]\displaystyle{ f(a) }[/math]에서 [math]\displaystyle{ f(b) }[/math]까지 변한다. 이때 [math]\displaystyle{ x }[/math]값의 변화량을 [math]\displaystyle{ \Delta x:=b-a }[/math], [math]\displaystyle{ \Delta y:=f(b)-f(a) }[/math]로 나타낸다. 이때 [math]\displaystyle{ \frac{\Delta y}{\Delta x} = \frac{f(b)-f(a)}{b-a} = \frac{f(a+\Delta x) - f(a)}{\Delta x} }[/math]를 [math]\displaystyle{ x }[/math]의 값이 [math]\displaystyle{ a }[/math]에서 [math]\displaystyle{ b }[/math]까지 변할 때 [math]\displaystyle{ y=f(x) }[/math]의 평균변화율이라 한다. 기하학적으로 생각한다면 [math]\displaystyle{ (a,f(a)) }[/math]와 [math]\displaystyle{ (b,f(b)) }[/math]를 잇는 직선의 기울기가 평균변화율이 된다.

여기서 [math]\displaystyle{ \Delta x \to 0 }[/math]일 때, 평균변화율의 극한값 [math]\displaystyle{ \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{f(a+\Delta x) - f(a)}{\Delta x} }[/math]이 존재하면 [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ x=a }[/math]에서 미분가능(differentiable at a)한다. 또한 이 극한값을 [math]\displaystyle{ x=a }[/math]에서의 f의 미분계수(derivative of f at a)라 하고 기호로 [math]\displaystyle{ f'(a) }[/math]라 표현한다. 참고로 differential coefficient라는 표현은 적절치 않다고 사용하지 말라는 학자가 있다. 기하학적으로 생각한다면 [math]\displaystyle{ x=a }[/math]에서의 접선의 기울기가 미분계수가 된다.

도함수

함수 [math]\displaystyle{ f: [a,b] \to \Bbb{R} }[/math]에 대하여 함수 [math]\displaystyle{ f }[/math]가 미분가능한 점 [math]\displaystyle{ x \in [a,b] }[/math]전체의 집합을 E라고 하면 E의 각 점 [math]\displaystyle{ x }[/math]에 대하여 그 점에서의 미분계수[math]\displaystyle{ f'(x) }[/math]를 대응시킬 수 있다. 여기서 함수 [math]\displaystyle{ f }[/math]에 대하여 새로운 함수[math]\displaystyle{ g: E \to \Bbb{R} }[/math]을 [math]\displaystyle{ g(x)=f'(x) }[/math]로 정의할 때, 이 함수 [math]\displaystyle{ g }[/math]를 [math]\displaystyle{ f }[/math]의 도함수(derived function of f, derivative of f)라고 하고 이를 기호로 [math]\displaystyle{ f' }[/math] 또는 [math]\displaystyle{ \frac{df}{dx} }[/math]로 나타낸다.

다항식의 미분

추가바람