Fano's Geometry
설명[편집 | 원본 편집]
결합 기하학의 모델 중 하나. 이탈리아의 수학자인 지노 파노(Gino Fano)의 이름을 딴 것이다. 일단 구조를 먼저 살펴보자.
- 점: A, B, C, D, E, F, G
- 선: {A, B, C}, {C, D, E}, {E, F, A}, {A, G, D}, {C, G, F}, {E, G, B}, {B, D, F}
이제, 이 구조가 결합 기하학의 세 공리를 만족함을 보이자.
- 임의의 두 점에 대해 그 두 점을 지나는 유일한 선이 존재한다.
- 7개의 점 중 2개를 고르는 가짓수는 21가지 이다. 직접 체크해 보자(...).
- 임의의 선에 대해, 그 선 위에 서로 다른 두 점이 존재한다.
- 선이 7개 존재하고, 모든 선에 정확히 3개의 서로 다른 점이 존재하므로 성립한다.
- 공선점이 아닌 세 점이 존재한다.
- A, B, D를 모두 지나는 선은 존재하지 않는다.
- 주어진 시스템이 I1, I2, I3을 만족하므로, 이 기하학은 결합 기하학의 모델이다.
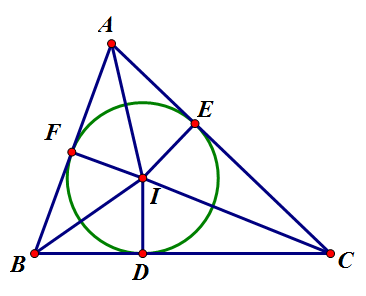
파노 기하학을 시각화하면 아래 그림과 같다.
점 I를 G로 바꾸고, A부터 시계 반대 방향으로 점을 B, C, D, E, F로 바꾸면 위 설명과 동일한 구조가 된다.
특징[편집 | 원본 편집]
얼핏 보면 파노 기하학은 점의 개수만 늘어났을 뿐, 세 점 기하학과 별반 다른 것이 없다고 생각할 수 있으나, 파노 기하학은 모든 선이 정확히 3개의 점을 가지는 가장 간단한 결합 기하학이다. 이를 증명해 보자 (직접 그림을 그리면서 해보면 이해가 쉬울 것이다).
- I3에 의해, 적어도 3개의 점을 가져야 한다. 그런데 모든 선이 3개의 점을 가져야 하므로, 이 3점은 공선점이다. 그런데 이는 공선점이 아닌 세 점이 존재해야 한다는 I3에 모순이므로, 점 3개 만으로는 조건을 만족할 수 없다.
- 네 점 A, B, C, D가 존재한다고 가정하자. 먼저, A, B, C를 잇자. I1에 의해, A와 D를 지나는 선이 존재해야 한다. 그런데, 모든 선은 3개의 점을 가지므로, 이 선은 B 또는 C를 지나야 한다. 일반성을 잃지 않고 B를 지난다고 가정하자. 그럼, A와 B를 지나는 선은 {A, B, C}, {A, B, D}의 두 개이며, 이 두 선은 서로 다르다. 그리고 이는 I1의 유일성에 모순이다. 따라서 점 4개 만으로는 모든 조건을 만족할 수 없다.
- 5점 A, B, C, D, E가 존재한다고 가정하자. 먼저, A, B, C를 잇자. I1에 의해 A와 D를 지나는 선이 존재해야 하고, 점이 4개일 경우를 고려하면, 이 선은 E를 지나야만 한다. 이제, B와 D를 이어야 하는데, 모든 선은 3점을 지나므로, 이 선은 A, C, E 중 하나를 지난다. 그런데 어느 경우든 I1의 유일성에 모순이다. 따라서 점 5개 만으로는 모든 조건을 만족할 수 없다.
- 6점 A, B, C, D, E, F가 존재한다고 가정하자. A, B, C를 잇고, A와 D를 지나는 선이 일반성을 잃지 않고 E를 지난다고 가정하자. 이제 E와 F를 이어야 하는데, 이 선이 A나 D를 지나면 I1의 유일성에 모순이 되므로, 이 선은 B나 C를 지나야 한다. 일반성을 잃지 않고 C를 지난다고 가정하자. 이제, A와 F를 이어야 한다. 그런데, B, C, D, E 어느 점을 지나든 I1의 유일성에 모순이다. 따라서, 점 6개만으로는 모든 조건을 만족할 수 없다.
- 점 7개가 존재하면 파노의 기하학이 한 예이다. 이제 선 7개가 가능한 가장 적은 수임을 보여야 하는데, 노가다로 보일 수도 있지만, 약간 편법을 사용해 보자. 위 시각화된 그림에서, 아무 선이나 하나 제거해 보자. 그럼 I1의 두 점을 지나는 선의 존재성에 문제가 생긴다. 결국 아무 선도 지울 수 없으므로, 7개가 최소라고 생각할 수 있다(...).