공선점

Collinearity, Colinearity

개요

평면, 혹은 임의의 n차원 하이퍼스페이스에 존재하는 점들이 한 직선 위에 존재하면, 그 점들을 공선점이라 부른다. 영어로는 "Collinearity"라고 하며, "Colinearity"(l이 하나)로 써도 맞는 표현으로 취급한다. 어떤 점들이 공선점인지 밝혀내는 것은 평면기하학의 핵심이며, 공원점과 함께 수학 경시대회 기하학 파트의 필수요소.

증명 방법

당연하지만 수학에서는 "그려봤는데 한 직선 위에 있더라"같은 논리는 통하지 않는다. 직접 그려서 확인하는 것은 공선점이라고 추측할 수 있는 단서가 되지만, 실제로 공선점임을 보이기 위해서는 수학적인 방법을 사용해야 한다. 이 문단에서는 특별한 말이 없는 한, 세 점 [math]\displaystyle{ A,P,B }[/math]가 공선점임을 보일 수 있는 방법을 소개한다.

기본

1. [math]\displaystyle{ \angle{APB}=180^\circ }[/math]: 각도가 평각이면 곧 직선임을 의미하므로 세 점은 공선점이 된다. 보통 제일 첫번째로 시도하는 방법이다. 다만 [math]\displaystyle{ \angle{APB}=180^\circ }[/math]을 바로 보이기는 힘드므로 어떤 점 [math]\displaystyle{ C }[/math]를 기준으로 하여 [math]\displaystyle{ \angle{APC}+\angle{BPC}=180^\circ }[/math]를 보이게 된다.

2. 맞꼭지각: 위 1번 방법과 근본적으로는 같은 방법. [math]\displaystyle{ C,P,D }[/math]가 공선점임을 알고 있을 때, [math]\displaystyle{ \angle{APC}=\angle{BPD},\,\angle{APD}=\angle{BPD} }[/math]를 보이면 된다. 두 맞꼭지각이 동시에 성립하면 직선이 되어야하기 때문.

3. 두 점이 동일함을 증명: 무슨 소리냐 하면, [math]\displaystyle{ A,P',B }[/math]가 이미 공선점임을 알고 있을 때, [math]\displaystyle{ P=P' }[/math]임을 보여 [math]\displaystyle{ A,P,B }[/math]도 공선점임을 보이는 방법이다. 대표적으로 메넬라우스의 정리의 역을 증명할 때 사용 되는 방법. 하지만 이 방법은 사용하기가 까다롭기 때문에 자주 쓰이지 않는다.

4. [math]\displaystyle{ \overline{AB}=\overline{AP}+\overline{BP} }[/math]: 삼각부등식에서 등호가 성립하려면 세 점이 공선점이어야 한다는 사실을 이용한다. 만약 세 점이 공선점이 아니면 반드시 [math]\displaystyle{ \overline{AB}\lt \overline{AP}+\overline{BP} }[/math]가 성립하게 된다.

5. 해석기하학: [math]\displaystyle{ \overline{AB} }[/math]의 방정식과 [math]\displaystyle{ P }[/math]의 좌표를 직접 구한 뒤, 직선의 방정식에 [math]\displaystyle{ P }[/math]의 좌표를 넣었을 때 성립하는지 확인한다. 해석기하학이 다 그렇듯이 노가다가 필수지만, 시간을 투자하면 확실하게 공선점인지 파악할 수 있다.

6. 벡터: 기하학의 사기 아이템, 벡터를 사용하여 공선점 여부를 파악할 수 있다. 두 벡터가 평행하고, 시점이 같다면 두 벡터의 시점과 종점은 한 직선 위에 있게 된다. 혹은 두 벡터가 평행하고, 첫번째 벡터의 종점과 두번째 벡터의 시점이 같아도 역시 공선점이 된다. 위 해석기하학적 방법과 이 방법은 일반적인 n차원에 대해서도 쉽게 쓸 수 있다는 장점이 있다. 하지만 공선점을 활용하는 문제는 거의 다 평면기하학

심화

1. 메넬라우스의 정리의 역: [math]\displaystyle{ \triangle{ABC} }[/math]와 세 점 [math]\displaystyle{ D,E,F }[/math]에 관해 [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이 성립하면, [math]\displaystyle{ D,E,F }[/math]는 공선점이다. 이걸 도대체 무슨 수로 써먹냐는 생각이 들 수 있는데, 공선점임을 증명하는 문제에 거의 반드시 사용된다고 보면 된다.

2. 메넬라우스의 정리(삼각함수)의 역: [math]\displaystyle{ \triangle{ABC} }[/math]와 세 점 [math]\displaystyle{ D,E,F }[/math]에 관해 [math]\displaystyle{ \frac{\sin{AEF}}{\sin{EFA}}\cdot\frac{\sin{DFB}}{\sin{BDF}}\cdot\frac{\sin{CDE}}{\sin{DEC}}=1 }[/math]이 성립하면, [math]\displaystyle{ D,E,F }[/math]는 공선점이다. 네?

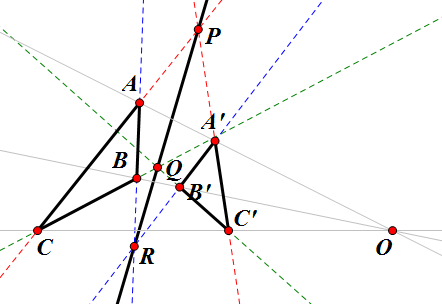
3. 데자르그의 정리: [math]\displaystyle{ \triangle{ABC} }[/math]와 [math]\displaystyle{ \triangle{A'B'C'} }[/math]에서, 세 직선 [math]\displaystyle{ \overleftrightarrow{AA'},\overleftrightarrow{BB'},\overleftrightarrow{CC'} }[/math]가 한 점 [math]\displaystyle{ O }[/math]에서 만나고, 직선 [math]\displaystyle{ \overleftrightarrow{BC},\overleftrightarrow{B'C'} }[/math]의 교점을 [math]\displaystyle{ P }[/math], 직선 [math]\displaystyle{ \overleftrightarrow{CA},\overleftrightarrow{C'A'} }[/math]의 교점을 [math]\displaystyle{ Q }[/math], 직선 [math]\displaystyle{ \overleftrightarrow{AB},\overleftrightarrow{A'B'} }[/math]의 교점을 [math]\displaystyle{ R }[/math]이라 하면, [math]\displaystyle{ P,Q,R }[/math]는 공선점이다. 뭐라고요? 증명은 메넬라우스의 정리의 역을 사용한다. 참고로 이 정리는 삼차원 공간에 대해서도 성립한다.

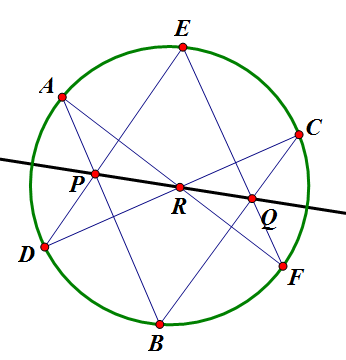
4. 파스칼의 정리: [math]\displaystyle{ A,B,C,D,E,F }[/math]를 한 원 위의 점들이라 하자. 현 [math]\displaystyle{ \overline{AB},\overline{DE} }[/math]의 교점을 [math]\displaystyle{ P }[/math], 현 [math]\displaystyle{ \overline{BC},\overline{EF} }[/math]의 교점을 [math]\displaystyle{ Q }[/math], 현 [math]\displaystyle{ \overline{CD},\overline{AF} }[/math]의 교점을 [math]\displaystyle{ R }[/math]이라 하면 [math]\displaystyle{ P,Q,R }[/math]는 공선점이다. ??? 증명은 메넬라우스의 정리의 역과 방멱의 정리를 사용한다. 참고로 두 현이 평행하면 명제는 성립하지 않는다. 또한, 이 정리는 원이 아니니라 다른 이차곡선에 대해서도 성립하며, 두 현이 만나지 않는다면 연장하면 된다. 그리고 직선 [math]\displaystyle{ \overleftrightarrow{PQR} }[/math]을 파스칼 선이라 부른다.

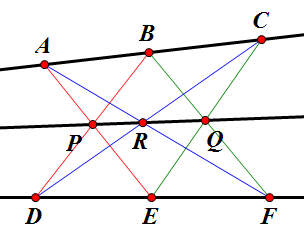
5. 파푸스의 육각형 정리: [math]\displaystyle{ A,B,C }[/math]를 한 직선 위의 점, [math]\displaystyle{ D,E,F }[/math]를 다른 직선 위의 점들이라 하자. [math]\displaystyle{ \overline{AE},\overline{BD} }[/math]의 교점을 [math]\displaystyle{ P }[/math], [math]\displaystyle{ \overline{BF},\overline{CE} }[/math]의 교점을 [math]\displaystyle{ Q }[/math], [math]\displaystyle{ \overline{AF},\overline{CD} }[/math]의 교점을 [math]\displaystyle{ R }[/math]이라 하면, [math]\displaystyle{ P,Q,R }[/math]은 공선점이다. ????? 증명은 메넬라우스의 정리를 다섯번 쓰면 된다.

6. 심슨의 정리: [math]\displaystyle{ \triangle{ABC} }[/math]의 외접원 위의 임의의 점 [math]\displaystyle{ P }[/math]에서 세 변(혹은 그 연장선)에 내린 수선의 발을 [math]\displaystyle{ D,E,F }[/math]라 하자. 그럼 [math]\displaystyle{ D,E,F }[/math]는 공선점이다. 증명은 각도가 [math]\displaystyle{ 180^\circ }[/math]임을 보이는 것이 제일 쉽다. 메넬라우스의 정리의 역을 쓸 수도 있지만 그러면 너무 복잡해진다. 참고로 직선 [math]\displaystyle{ \overleftrightarrow{DEF} }[/math]를 점 [math]\displaystyle{ P }[/math]에 대한 심슨선이라 부르며, 보기만 해도 정신이 날아갈 듯한 3, 4, 5번 증명과는 달리 자주 쓰인다.

공선점 예시

• 한 점과, 그 점을 점대칭시킨 점과, 대칭점.
• 외심, 무게중심, 수심, 구점원의 중심. 오일러 직선이라 부른다.
• 삼각형의 한 꼭짓점, 내심, 그 꼭짓점에 대한 방심.
• 삼각형의 한 꼭짓점, 나머지 두 꼭짓점에 대한 방심.

관련 항목

• 선 (수학)
• 공원점