완전대각방진

개요

완전대각방진(Pandiagonal Magic Square)는 마방진 중에서 기본적인 대각선 뿐만 아니라 그 대각선과 평행한 대각선들 상의 원소의 합도 모두 동일한 마방진을 의미한다.

완전대각방진 만들기

참고로 변의 칸의 개수가 3개이거나 4n+2꼴일 때에는 만들 수 없다.

한 변의 개수가 6n±1개인 경우

이와 관련한 내용은 마방진#홀수 방진에서 볼 수 있습니다.

마방진 문서의 홀수 마방진을 만드는 방법을 일반화하는 방법을 이용해서 완전대각방진을 만들 수 있다.

일단 이변수 함수
T:{1,..,n}×{1,...,n} → {1,2,...,n²} , T(a,b)=(a-1)n+b
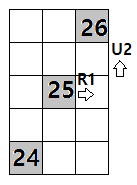
형태로 잡는다. 그러면 T는 일대일 대응인 것을 쉽게 보일 수 있다. 우선 홀수방진은 정가운데 칸 (즉 (n+1)/2열 (n+1)/2행)이 존재한다. 이곳에 k=(n²+1)/2=T((n+1)/2, (n+1)/2)를 집어넣는다. 그 다음에 2줄/1칸 위, 즉 날 일자(日), 혹은 체스의 나이트(knight) 행마와 유사한 형태로 k+1=T((n+1)/2,(n+3)/2)을, 반대로 2줄/1칸 아래 방향으로는 k-1=T((n+1)/2,(n-1)/2)를 집어넣는다. 아래의 그림을 참조하자.

위의 마방진 채우듯 맨 윗줄을 넘길 경우 맨 아랫줄로 넘기고, 맨 오른쪽 칸을 넘길 경우 맨 왼쪽 칸으로 숫자를 옮긴다. 이와 마찬가지 방법으로 k-(n-1)/2=T((n+1)/2,1) 부터 k+(n-1)/2 = T((n+1)/2, n)까지 채운다.

그 다음에 k-(n-1)/2+1=T((n-1)/2,n)은 k-(n-1)/2=T((n+1)/2,1)의 1칸 오른쪽/1칸 아래에, k+(n+1)/2=T((n+3)/2, 1)은 k+(n-1)/2 = T((n+1)/2,n)의 1칸 왼쪽/1칸 위에 적는다. 역시 아래의 그림을 참조하자. 이와 같은 방법으로 T(a,k), k=1,...n이 완성되었을 때 T(a,k)의 1칸 왼쪽/1칸 위에 T(a+1, k+1) (k=n이면 k+1은 1로 간주), T(a,k)의 1칸 오른쪽/1칸 아래에 T(a-1,k-1) (k=1이면 k-1=n으로 간주)가 적힌다.

이러한 방법으로 1=T(1,1)부터 n²=T(n,n)까지 채울 수 있다. 여기서 위의 그림처럼 T(a,b)와 T(a,b+1)의 간격이 가로/세로 모두 n과 서로소이고, T(a,n)에서 T(a+1,1)의 이동간격도 가로/세로가 모두 n과 서로소이면서 두 개의 이동간격이 서로 겹치지 않을 때 마방진이 형성된다. 왜냐하면 각 마방진에서 T^-1(n)∈[n]×[n]을 고려하면 격자점의 집합 {(k,l)}은 같은 행/같은 열에서 k값과 l값이 일치할 수 없기 때문이다. 즉 i 또는 j 중 하나가 고정되고 나머지 변수로 움직인다고 가정할 때 집합
{T^-1(X_ij)=(a_i1,b_ij)}
는 h≠i일 때 a_ij≠a_hj, b_ij≠b_hj, k≠j일 때 a_ij≠a_ik, b_ij≠b_ik임을 통해 각각 [n]*[n]상에서 같은 행/열에 2개 이상의 원소가 존재하지 않는 n개의 격자점의 배열이 된다.

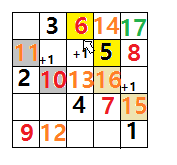
특히 위의 방식을 이용해 유도된 마방진은 n=6a+3 형태가 아닐 때(즉 6a±1 형태일 때) 완전대각방진(Panmagic Square)을 이룬다. 가로, 세로 대각선 모두 5×5 예제와 7×7 예제를 살펴보자.

5×5 완전대각방진

25	3	6	14	17
11	19	22	5	8
2	10	13	16	24
18	21	4	7	15
9	12	20	23	1

7×7 완전대각방진

49	23	4	34	8	38	19
11	41	15	45	26	7	30
22	3	33	14	37	18	48
40	21	44	25	6	29	10
2	32	13	36	17	47	28
20	43	24	5	35	9	39
31	12	42	16	46	27	1

한 변의 개수가 6n+3개인 경우

(6n+3)*(6n+3) 완전대각방진은 위와 같은 방법으로 만들 수 없다. 고로 아래와 같은 방법을 사용해야 한다.

• 우선 왼쪽 위의 (2n+1)×3 형태의 사각형 안에 1부터 6n+3까지의 자연수를 채운다. 여기서 주의할 점은 3개의 열은 모두 원소의 합이 동일해야 한다는 것이다. 아래와 같이 만들 수 있다.

Examples:

For 9×9 square   1    2    3   5   6   4   9   7   8  vertical sum = 15

For 15×15 square   1    2    3   5   6   4   9   7   8   10   11   12   15   14   13  vertical sum = 40

For 21×21 square   1    2    3   5   6   4   9   7   8  10 11 12 15 14 13 16 17 18 21 20 19 vertical sum = 77

• 아래의 2n+1×3 패턴을 각각 2개씩 복사해서 아랫줄을 채운다.

Example:

1	2	3
5	6	4
9	7	8
1	2	3
5	6	4
9	7	8
1	2	3
5	6	4
9	7	8

• 다음 오른쪽 3열에 왼쪽의 패턴을 복사한다. 단 왼쪽의 숫자 패턴을 그대로 복사하지 말고, 한 줄씩 아래로 내려야 한다.

Example:

1	2	3	9	7	8
5	6	4	1	2	3
9	7	8	5	6	4
1	2	3	9	7	8
5	6	4	1	2	3
9	7	8	5	6	4
1	2	3	9	7	8
5	6	4	1	2	3
9	7	8	5	6	4

• 마찬가지로 다음 오른쪽 3열에 바로 왼쪽의 3열 패턴을 한 열씩 내린 상태로 복사한다. 이런 식으로 행렬을 채울 경우 한 행에 1부터 6n+3까지 하나씩 들어가게 된다.

Example:

1	2	3	9	7	8	5	6	4
5	6	4	1	2	3	9	7	8
9	7	8	5	6	4	1	2	3
1	2	3	9	7	8	5	6	4
5	6	4	1	2	3	9	7	8
9	7	8	5	6	4	1	2	3
1	2	3	9	7	8	5	6	4
5	6	4	1	2	3	9	7	8
9	7	8	5	6	4	1	2	3

• 위에서 생성한 행렬의 전치행렬(transpose)을 만든다. 즉, 위의 행렬에서 (i,i)로 구성된 대각선을 기준으로 원소를 뒤집는 행렬을 만든다.

Example:

A   1    2    3    9    7    8    5    6    4   5   6   4   1   2   3   9   7   8   9   7   8   5   6   4   1   2   3   1   2   3   9   7   8   5   6   4   5   6   4   1   2   3   9   7   8   9   7   8   5   6   4   1   2   3   1   2   3   9   7   8   5   6   4   5   6   4   1   2   3   9   7   8   9   7   8   5   6   4   1   2   3

AT   1    5    9    1    5    9    1    5    9   2   6   7   2   6   7   2   6   7   3   4   8   3   4   8   3   4   8   9   1   5   9   1   5   9   1   5   7   2   6   7   2   6   7   2   6   8   3   4   8   3   4   8   3   4   5   9   1   5   9   1   5   9   1   6   7   2   6   7   2   6   7   2   4   8   3   4   8   3   4   8   3

• 마지막으로 행렬은 A의 원소와 (B의 원소-1)에 (6n+3)배를 더하면 된다. 이 행렬은 완전대각행렬이 된다.

Example: A + (6n+3)×A^T – (6n+3)

1	38	75	9	43	80	5	42	76
14	51	58	10	47	57	18	52	62
27	34	71	23	33	67	19	29	66
73	2	39	81	7	44	77	6	40
59	15	49	55	11	48	63	16	53
72	25	35	68	24	31	64	20	30
37	74	3	45	79	8	41	78	4
50	60	13	46	56	12	54	61	17
36	70	26	32	69	22	28	65	21

한 변의 개수가 4n개인 경우

이와 관련한 내용은 마방진#4n형태에서 볼 수 있습니다.

• 첫번째 줄, 1부터 2n열까지 1부터 2n까지 1씩 올려서 숫자를 채운다.

1	2	3	4

• 숫자를 채운 줄 아래에 2n+1부터 4n까지 숫자를 채운다. 여기서 숫자를 적은 열의 두 원소의 합은 정확히 4n+1이 되어야 한다.

Example:

1	2	3	4
8	7	6	5

• 1/2행의 숫자를 적은 패턴대로 아래처럼 아랫쪽 행에도 2n개씩 복사한다. 모든 행, 2n까지의 열을 채운다.

Example:

1	2	3	4
8	7	6	5
1	2	3	4
8	7	6	5
1	2	3	4
8	7	6	5
1	2	3	4
8	7	6	5

• 역시 왼쪽 반을 채운 패턴대로 오른쪽 절반도 채운다. 다만 여기서는 각 행/열의 합을 맞추기 위해 왼쪽의 패턴과는 행이 하나씩 어긋나게 채워야 한다.

Example:

1	2	3	4	8	7	6	5
8	7	6	5	1	2	3	4
1	2	3	4	8	7	6	5
8	7	6	5	1	2	3	4
1	2	3	4	8	7	6	5
8	7	6	5	1	2	3	4
1	2	3	4	8	7	6	5
8	7	6	5	1	2	3	4

• 이제 두 번째 4n*4n 행렬은 첫 번째 4n*4n행렬을 왼쪽으로 90도 회전한 형태로 만든다.

Square A   1    2    3    4    8    7    6    5    8    7    6    5    1    2    3    4    1    2    3    4    8    7    6    5    8    7    6    5    1    2    3    4    1    2    3    4    8    7    6    5    8    7    6    5    1    2    3    4    1    2    3    4    8    7    6    5    8    7    6    5    1    2    3    4

Square B   5    4    5    4    5    4    5    4    6    3    6    3    6    3    6    3    7    2    7    2    7    2    7    2    8    1    8    1    8    1    8    1    4    5    4    5    4    5    4    5    3    6    3    6    3    6    3    6    2    7    2    7    2    7    2    7    1    8    1    8    1    8    1    8

• 이제 첫 번째 행렬 A의 숫자와 두 번째 행렬 B의 원소에서 1을 뺀 뒤에 4n을 곱한 숫자를 더한다. 그러면 완전대각행렬이 완성된다.

Example: A + 4n×B - 4n

33	26	35	28	40	31	38	29
48	23	46	21	41	18	43	20
49	10	51	12	56	15	54	13
64	7	62	5	57	2	59	4
25	34	27	36	32	39	30	37
24	47	22	45	17	42	19	44
9	50	11	52	16	55	14	53
8	63	6	61	1	58	3	60

• 이것이 완전대각행렬임을 보이는 방법은 다음과 같다.
  • 우선 첫 번째 정사각행렬 A는 가로줄이 1~4n까지 하나씩 들어가 있음을 알 수 있다.
  • 또한 첫 번째 정사각행렬 A는 세로줄에서는 {1,4n}, {2,4n-1},... {2n,2n+1} 패턴이 2n번 반복하는 것을 알 수 있으며, 역시 각 세로줄의 원소의 합은 4n(4n+1)/2가 되는 것을 알 수 있다.
  • ↘ 방향 대각선의 경우에는(홀줄/짝줄) 왼쪽 절반의 원소는 인접한 두 원소의 합이 4n, 오른쪽 절반의 원소는 인접한 두 원소의 합이 4n+2가 된다. 미묘하게 {2n,1}이 엮인 경우가 생길 수 있으나 계속 내려가다 보면 {2n+1, 4n}이 엮이는 경우가 하나 더 생긴다. 따라서 대각선의 합은 모두 동일하게 된다. 이는 ↙ 방향 대각선의 경우도 마찬가지.
  • 따라서 행렬 A는 가로/세로/대각선 상의 원소의 합이 모두 동일하다. 마찬가지로 행렬 B는 A의 회전으로 인해 만들어진 패턴이므로 가로/세로/대각선 상의 원소의 합이 동일함을 알 수 있다.
  • 이제 A 상에서 k값을 가진 좌표가 B 상에서는 {1,2,...,4n}과 하나씩 상응함을 보이면 된다. 우선 A상에서 값을 t(t≤2n)로 하는 좌표는 (1,t),(2,2n+t),(3,t),...,(2k-1,t),(2k,2n+t),...,(4n-1,t),(4n,2n+t)가 된다. 그러나 B(a,b)=A(4n+1-a)이므로 B(2k-1,t)=A(4n+1-t,2k-1)=A(2n+1-t,2k-1), B(2k,2n+t)=A(2n+1-t,2k)가 된다. 즉, k=1,..,2n까지 움직일 경우 행 2n+1-t상의 모든 값을 생성할 수 있으며, 이는 1부터 4n까지의 모든 원소를 채우게 된다는 것을 알 수 있다.

이 문서의 전체 혹은 일부는 마방진 문서의 409765판에서 가져왔습니다.

이 문서에는 영어판 위키백과의 Pandiagonal Magic Square 문서 일부 판을 번역한 내용이 포함되어 있습니다.