독일 천문학자 케플러는 그의 스승인 브라헤가 죽기 직전 짧은 기간동안 브라헤의 조수였는데, 스승의 자료를 받아 16년만에 행성들의 움직임에 관한 수학적 모형을 이끌어냈다.
행성의 운동에 대한 케프러의 완전한 해석은 케플러의 법칙 이라는 다음의 세법칙으로 요약할 수 있다.
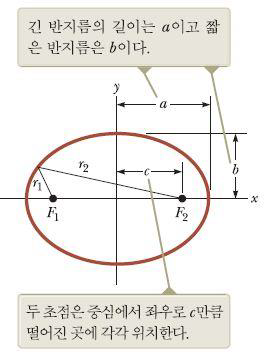
1. 모든 행성들은 태양을 한 초점으로 하는 타원 궤도를 따라서 이동한다.
2. 태양과 행성을 잇는 반지름 벡터는 같은 시간 간격 동안에 같은 넓이를 쓸고 지나간다.
3. 모든 행성의 궤도 주기의 제곱은 그 행성 궤도의 긴 반지름의 세제곱에 비례한다.
케플러의 제1법칙
중력의 거리 제곱에 반비례하는 성질의 결과이다.
원은 타원의 특별한 형태로 해석할 수 있다.
케플러의 제2법칙
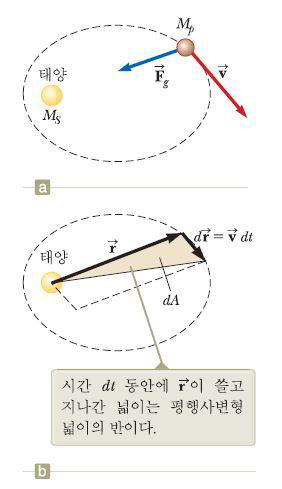
각운동량 보존의 결과로 설명할 수 있다. 태양이 행성에 비해 훨씬 더 큰 질량을 가지고 있으면, 태양은 움직이지 않는다고 가정한다. 태양이 행성에 작용하는 중력은 중심력이며, 태양을 향하는 반지름 방향이다.
[math]\displaystyle{ \tau = r\times {F}_{g} = 0 }[/math]
[math]\displaystyle{ L = r\times p = {M}_{p}r\times v = }[/math] 일정
그림 b에서 반지름 벡터 [math]\displaystyle{ \vec{r} }[/math]은 시간 dt동안 넓이 dA를 쓸고 지나가는데 이 넓이는 벡터 [math]\displaystyle{ \vec{r} }[/math]과 [math]\displaystyle{ d\vec{r} }[/math]이 만든 평행사변형의 넓이 [math]\displaystyle{ \left|\vec{r}\times d\vec{r} \right| }[/math]의 반이다. 시간 dt동안 행성이 지나간 거리는 [math]\displaystyle{ d\vec{r} = \vec{v}dt }[/math]이므로
[math]\displaystyle{ dA = \frac{1}{2}\left|\vec{r}\times d\vec{r} \right| = \frac{1}{2}\left|\vec{r}\times \vec{v}dt \right| = \frac{L}{{2M}_{p}dt} }[/math]
[math]\displaystyle{ \frac{dA}{dt} = \frac{L}{{2M}_{p}} }[/math]
여기서 L과 Mp는 모두 상수이다.
케플러의 제3법칙
행성이 원운동할 때 행성의 구심 가속도를 제공하는 것이 중력이므로, 등속 원운동을 하는 물체에 뉴턴의 제2법칙을 적용하면
[math]\displaystyle{ {F}_{g} = \frac{G{M}_{s}{M}_{p}}{{r}^{2}} = {M}_{p}a = \frac{{M}_{p}{v}^{2}}{r} }[/math]
[math]\displaystyle{ v = \frac{2\pi r}{T} }[/math](T:주기)이므로
[math]\displaystyle{ \frac{G{M}_{s}}{{r}^{2}} = \frac{\left(2\pi r/T \right)}{r} }[/math]
[math]\displaystyle{ {T}^{2} = \left(\frac{4{\pi }^{2}}{G{M}_{s}} \right){r}^{3} = {K}_{s}{r}^{3} }[/math]
타원 궤도인 경우에는 r을 긴 반지름 a로 바꾸면 된다.
[math]\displaystyle{ {T}^{2} = \left(\frac{4{\pi }^{2}}{G{M}_{s}} \right){a}^{3} = {K}_{s}{a}^{3} }[/math]