잔글 (→부정적분과 정적분) |
잔글편집 요약 없음 |
||
| 40번째 줄: | 40번째 줄: | ||
그리고 <math>[a,b]</math>의 분할 전체의 집합을 <math>\mathcal{P}[a,b]</math>라 하자. 실수의 완비성 공리에 의하여 | 그리고 <math>[a,b]</math>의 분할 전체의 집합을 <math>\mathcal{P}[a,b]</math>라 하자. 실수의 완비성 공리에 의하여 | ||
<math>\sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\}, \ \inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\}</math>는 존재하고 이때, <math>\ | <math>\sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\}, \ \inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\}</math>는 존재하고 이때, <math>\inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\} =\overline{\int_{a}^{b}} f(x) \, dx</math>을 리만 상적분(upper Riemann intergral), <math>\sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\} = \underline{\int_{a}^{b}} f(x) \, dx</math>를 리만 하적분(lower Riemann integral)이라고 한다. 그리고 <math>\underline{\int_{a}^{b}} f(x) \, dx = \overline{\int_{a}^{b}} f(x) \, dx</math>이면 리만 적분 가능(Riemann integrable)하다고 하며 그 값을 <math>\int_{a}^{b} f(x)\, dx</math>로 표현한다. | ||
리만합 | 리만합 | ||
| 52번째 줄: | 52번째 줄: | ||
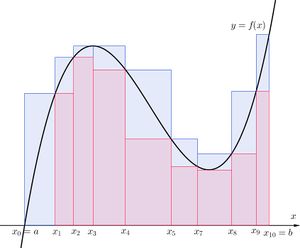
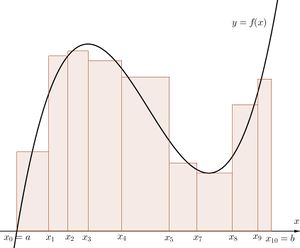
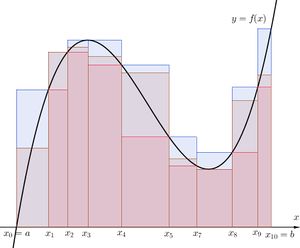
[[파일:U l r sum.jpg|섬네일|같은 분할에 대한 상합(파란 사각형)과 하합(빨간 사각형), 리만합(갈색 사각형)의 비교]] | [[파일:U l r sum.jpg|섬네일|같은 분할에 대한 상합(파란 사각형)과 하합(빨간 사각형), 리만합(갈색 사각형)의 비교]] | ||
상합, 하합과 리만합의 다른 점은 구간의 | 상합, 하합과 리만합의 다른 점은 상합은 구간의 상한, 하합은 구간의 하한, 리만합은 구간의 임의의 점을 선택했기 때문에 정의상 <math>L(f,P) \leq R(f,P) \leq U(f,P)</math>가 된다. 어떠한 정의를 사용하든 간에 결론은 구간을 세밀하게 분할하면 할수록, 상합과 하합, 리만합의 차이는 작아지게 되며 결국에는 극한을 취한다면 그 값은 하나로 결정된다는 것이다. 그 값을 <math>\int_{a}^{b} f(x)\, dx</math>라 표현하겠다는 것이다. | ||
===리만–스틸체스적분=== | ===리만–스틸체스적분=== | ||
2015년 5월 16일 (토) 23:03 판
미분을 거꾸로 하면 된다 카더라.
積分, Integration
개요
적분이라고 하면 당연히 정적분을 의미한다. 부정적분은 정의 자체가 미분의 역연산으로, 뭔가 새로운 개념이 아니다.
이와 달리 고등학교에서는 부정적분을 먼저 소개하는데, 이는 정의 자체가 미분의 역연산인 부정적분을 먼저 내보임으로써 기호와 이름이 비슷한 정적분도 미분이랑 뭔가 관계가 있겠지 하고 쉽게 받아들이게 하기 위한 일종의 눈속임(?)으로 보인다.
정적분은 미분과 하등의 관계가 없으며, 아래에서 언급할 여러 가지 방법으로 정의된다. 그런데 정적분을 계산할때, 부정적분을 이용하면 계산이 쉽더라는 뜨악한 정리가 바로 미적분학의 기본정리이다.
역사
도형의 넓이와 부피를 구하는 문제는 고대 이집트 시대부터 중요한 문제였는데, 케플러는 저서 '포도주통의 용적 측정'에서 한 축을 중심으로 원뿔곡선의 호를 회전시킨 도형 93개의 부피를 계산하는데 초기의 적분 개념을 이용하였다.
카빌리에리는 입체를 두께가 없는 평행한 면의 모임으로 생각하였으며 단면의 넓이를 비교하여 부피를 계산할 수 있었다. 이러한 방법을 '불가분량법(method of indivisibles)'이라고 하는데, 불가분량법은 그 당시 도형의 넓이나 부피를 구하는 데 널리 활용되었다.
뉴턴의 스승인 월리스는 논문 '무한의 수론(Arithemetica Infinitorum)'에서 데카르트와 카발리에리의 방법을 체계화하였다. 그는 [math]\displaystyle{ \int_{0}^{1} x^m \, dx = \frac{1}{m+1} }[/math]이 분수 m에 대해서도 성립함을 보였고, 곡선의 길이를 적분으로 구하는 식을 얻었다.
라이프니츠는 미적분에 대한 개념을 정립하면서 '미적분의 기본 정리(fundamental theorem of calculus)'를 발견하였고 미적분에 대한 많은 정리를 증명하였다. 그는 라틴어 summa의 첫문자 S를 길게 늘린 현대의 적분기호 [math]\displaystyle{ \int }[/math]을 처음으로 사용하였다.
미적분학을 체계화한 리만은 적분 가능성을 정의함으로써 함수를 적분 할 수 있다는 것이 무엇을 뜻하는 지를 명확히 하였다. 함수의 그래프와 x축 사이의 넓이는 x축을 잘게 자른 후 소구간 위에서 그래프의 위쪽(또는 아래쪽)에 직사각형을 만들어 이들의 넓이를 더한 값의 하한(또는 상한)과 같다는 것이 리만 적분의 기본적인 발상이다. 따라서 함수가 리만 적분가능하려면 극히 작은 구간에서 함숫값의 변화가 작아야 하며 이는 결국 함수의 연속성과 연관이 있게 된다.
르벡 적분의 기본적인 발상은 x축을 잘게 자르는 대신 y축을 잘게 잘라 함숫값이 y축의 소구간에 속하는 정의역의 점들의 집합을 생각하고 이 집합의 크기에 y축 소구간의 최댓값(또는 최솟값)을 곱하여 모두 더함으로써 넓이를 구하는 것이다. 이와 같은 개념을 엄밀히 이해하기 위해서는 측도(measure) 개념이 필요하다. 그러나 르베그 적분은 피적분함수의 연속성에 구애받지 않으므로 리만 적분에 비하여 더 넓은 범위의 함수를 적분할 수 있으며 수학적으로 여러가지 좋은 성질을 많이 가지고 있다.
구분구적법
리만적분
정의
상적분과 하적분
함수 [math]\displaystyle{ f:[a,b] \to \Bbb{R} }[/math]이 유계라 할 때, [math]\displaystyle{ [a,b] }[/math]의 임의의 분할 [math]\displaystyle{ P=\left\{ x_0 , x_1, \cdots , x_n \right\} }[/math]에 대하여 P의 각 소구간 [math]\displaystyle{ I_k=[x_{k-1},x_k] }[/math]에 대하여
[math]\displaystyle{ M(f,I_k) = \sup \left\{ f(x)|x \in I_k \right\} , \ m(f,I_k) = \inf \left\{ f(x)|x \in I_k \right\} }[/math]
라고 둔다. 구간에서 최댓값이나 최솟값을 사용하지 않고, 상한이나 하한을 쓴 이유는 함수가 불연속이어도 적분은 가능할 수 있기 때문이다.
그리고 다음과 같이 정의된 두 실수
[math]\displaystyle{ U(f,P) = \sum_{k=1}^n M(f,I_k) \Delta x_k, \ L(f,P) = \sum_{k=1}^n m(f,I_k) \Delta x_k }[/math]
를 각각 분할 P에 대한 f의 리만 상합(upper Riemann sum), 리만 하합(lower Riemann sum)이라고 한다.
그리고 [math]\displaystyle{ [a,b] }[/math]의 분할 전체의 집합을 [math]\displaystyle{ \mathcal{P}[a,b] }[/math]라 하자. 실수의 완비성 공리에 의하여 [math]\displaystyle{ \sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\}, \ \inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\} }[/math]는 존재하고 이때, [math]\displaystyle{ \inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\} =\overline{\int_{a}^{b}} f(x) \, dx }[/math]을 리만 상적분(upper Riemann intergral), [math]\displaystyle{ \sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\} = \underline{\int_{a}^{b}} f(x) \, dx }[/math]를 리만 하적분(lower Riemann integral)이라고 한다. 그리고 [math]\displaystyle{ \underline{\int_{a}^{b}} f(x) \, dx = \overline{\int_{a}^{b}} f(x) \, dx }[/math]이면 리만 적분 가능(Riemann integrable)하다고 하며 그 값을 [math]\displaystyle{ \int_{a}^{b} f(x)\, dx }[/math]로 표현한다.
리만합
함수 [math]\displaystyle{ f:[a,b] \to \Bbb{R} }[/math]이 유계라 할 때, [math]\displaystyle{ [a,b] }[/math]의 임의의 분할 [math]\displaystyle{ P=\left\{ x_0 , x_1, \cdots , x_n \right\} }[/math]에 대하여 [math]\displaystyle{ \lVert P \rVert = \max \left\{ \Delta x_k | k=1,2, \cdots, n \right\} }[/math]라 할때, 임의의 [math]\displaystyle{ t_k \in [x_{k-1},x_k] }[/math]에 대하여 [math]\displaystyle{ R(f,P)=\sum_{k=1}^n f(t_k) \Delta x_k }[/math]를 [math]\displaystyle{ [a,b] }[/math]의 분할 P에 대한 f의 리만합(Riemann sum)이라 한다.
이때 [math]\displaystyle{ \lim_{\lVert P \rVert \to 0}R(f,P) = \lim_{\lVert P \rVert \to 0} \sum_{k=1}^n f(t_k) \Delta x_k }[/math]의 극한이 존재하면 이를 리만 적분 가능(Riemann integrable)하다고 하고 [math]\displaystyle{ \lim_{\lVert P \rVert \to 0}R(f,P) = \int_{a}^{b} f(x)\, dx }[/math]로 표현한다.
차이
상합, 하합과 리만합의 다른 점은 상합은 구간의 상한, 하합은 구간의 하한, 리만합은 구간의 임의의 점을 선택했기 때문에 정의상 [math]\displaystyle{ L(f,P) \leq R(f,P) \leq U(f,P) }[/math]가 된다. 어떠한 정의를 사용하든 간에 결론은 구간을 세밀하게 분할하면 할수록, 상합과 하합, 리만합의 차이는 작아지게 되며 결국에는 극한을 취한다면 그 값은 하나로 결정된다는 것이다. 그 값을 [math]\displaystyle{ \int_{a}^{b} f(x)\, dx }[/math]라 표현하겠다는 것이다.
리만–스틸체스적분
르벡적분
참고문헌
- 우정호 외, 고등학교 미적분 I 교사용 지도서, 두산동아, 2014
- 황선욱 외 10인, 고등학교 미적분 I 교사용 지도서, (주)좋은책신사고, 2015
- 정동명·조승제, 실해석학 개론, 경문사, 2004