적분

틀:토막글 미분을 거꾸로 하면 된다 카더라.

積分, Integration

부정적분과 정적분

적분이라고 하면 당연히 정적분을 의미한다. 부정적분은 정의 자체가 미분의 역연산으로, 뭔가 새로운 개념이 아니다.

이와 달리 고등학교에서는 부정적분을 먼저 소개하는데, 이는 정의 자체가 미분의 역연산인 부정적분을 먼저 내보임으로써 기호와 이름이 비슷한 정적분도 미분이랑 뭔가 관계가 있겠지 하고 쉽게 받아들이게 하기 위한 일종의 눈속임(?)으로 보인다.

정적분은 미분과 하등의 관계가 없으며, 아래에서 언급할 여러 가지 방법으로 정의된다. 그런 적분의 역연산이 미분이라니!!! 하는 뜨악한 정리가 바로 미적분학의 기본정리이다.

그리고 부정적분은 전술했듯 정의 자체가 미분의 역연산이다. 그러니 미분과 하등의 관계가 없는 정적분은 부정적분과도 역시 아무런 관계가 없을 것임을 금방 알 수 있다. 이 둘을 연결지어 주는 것이 바로 고등학교 때 배우는 정적분의 기본정리인데, 이것까지 포함하여 미적분학의 기본정리라 하기도 한다.

리만적분

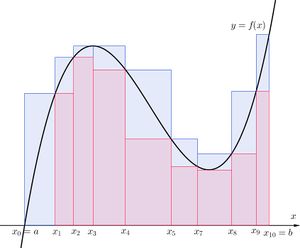
함수 [math]\displaystyle{ f:[a,b] \to \Bbb{R} }[/math]이 유계라 할 때, [math]\displaystyle{ [a,b] }[/math]의 임의의 분할 [math]\displaystyle{ P=\left\{ x_0 , x_1, \cdots , x_n \right\} }[/math]에 대하여 P의 각 소구간 [math]\displaystyle{ I_k=[x_{k-1},x_k] }[/math]에 대하여

상합(파란 사각형)과 하합(빨간 사각형)

[math]\displaystyle{ M(f,I_k) = \sup \left\{ f(x)|x \in I_k \right\} , \ m(f,I_k) = \inf \left\{ f(x)|x \in I_k \right\} }[/math]

라고 둔다. 구간에서 최댓값이나 최솟값을 사용하지 않고, 상한이나 하한을 쓴 이유는 함수가 불연속이어도 적분은 가능할 수 있기 때문이다.

그리고 다음과 같이 정의된 두 실수

[math]\displaystyle{ U(f,P) = \sum_{k=1}^n M(f,I_k) \Delta x_k, \ L(f,P) = \sum_{k=1}^n m(f,I_k) \Delta x_k }[/math]

를 각각 분할 P에 대한 f의 리만 상합(upper Riemann sum), 리만 하합(lower Riemann sum)이라고 한다.

그리고 [math]\displaystyle{ [a,b] }[/math]의 분할 전체의 집합을 [math]\displaystyle{ \mathcal{P}[a,b] }[/math]라 하자. 실수의 완비성 공리에 의하여 [math]\displaystyle{ \sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\}, \ \inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\} }[/math]는 존재하고 이때, [math]\displaystyle{ \sup \left\{ L(f,P) |P \in \mathcal{P}[a,b] \right\} }[/math]를 리만 하적분(lower Riemann integral), [math]\displaystyle{ \inf \left\{ U(f,P) |P \in \mathcal{P}[a,b] \right\} }[/math]을 리만 상적분(upper Riemann intergral)이라고 한다. 그리고 리만 상적분과 하적분의 값이 같을 때 리만 적분 가능(Riemann integrable)하다고 한다.

르벡적분

추가바람