잔글 (→증명) |
(→증명: 모바일 보기 문제 때문에 그림 순서 바꿉니다.) |
||
| 14번째 줄: | 14번째 줄: | ||
** <math>\deg x \le 4</math>일 때, v와 인접한 꼭짓점의 색은 최대 네 가지에 불과하므로, 인접한 꼭짓점의 색이 아닌 걸 적당히 골라서 ''x''에 색칠하면 된다. | ** <math>\deg x \le 4</math>일 때, v와 인접한 꼭짓점의 색은 최대 네 가지에 불과하므로, 인접한 꼭짓점의 색이 아닌 걸 적당히 골라서 ''x''에 색칠하면 된다. | ||
** <math>\deg x =5 </math>라고 하자. 이때, ''x''와 인접한 꼭짓점을 시계방향으로 <math>v_1,v_2,v_3,v_4,v_5</math>로 지정하고, 색을 1, 2, 3, 4, 5로 부여하자. ''G' ''의 부분그래프 <math>G_{1,3}</math>을 ''G' ''에서 색이 1과 3인 것을 모두 고르고 모서리로 연결한 그래프라고 하자. 이때 <math>G_{1,3}</math>에서 ''v''<sub>1</sub>에서 ''v''<sub>3</sub>로 가는 길이 없다면, ''v''<sub>1</sub>의 색을 ''v''<sub>3</sub>의 색으로 바꾸고 ''v''<sub>1</sub>과 연결된 점의 색 1, 3을 서로 바꾸면 된다. 그리고 ''x''를 1로 칠하면 된다. | ** <math>\deg x =5 </math>라고 하자. 이때, ''x''와 인접한 꼭짓점을 시계방향으로 <math>v_1,v_2,v_3,v_4,v_5</math>로 지정하고, 색을 1, 2, 3, 4, 5로 부여하자. ''G' ''의 부분그래프 <math>G_{1,3}</math>을 ''G' ''에서 색이 1과 3인 것을 모두 고르고 모서리로 연결한 그래프라고 하자. 이때 <math>G_{1,3}</math>에서 ''v''<sub>1</sub>에서 ''v''<sub>3</sub>로 가는 길이 없다면, ''v''<sub>1</sub>의 색을 ''v''<sub>3</sub>의 색으로 바꾸고 ''v''<sub>1</sub>과 연결된 점의 색 1, 3을 서로 바꾸면 된다. 그리고 ''x''를 1로 칠하면 된다. | ||
[[파일:Proofwhennotcycle.png|400px|가운데]] | |||
[[파일:proof13connected.png|섬네일|250px|음... <math>v_2,v_4</math>를 다른 모서리에 닿지 않고 연결하려면 {{ㅊ|지면을 뚫으면 되겠군}}그런 거 없다.]] | [[파일:proof13connected.png|섬네일|250px|음... <math>v_2,v_4</math>를 다른 모서리에 닿지 않고 연결하려면 {{ㅊ|지면을 뚫으면 되겠군}}그런 거 없다.]] | ||
:: <math>G_{1,3}</math>에서 ''v''<sub>1</sub>에서 ''v''<sub>3</sub>로 가는 길이 있다고 하자. 그러면 이제 얘 말고 ''G' ''에서 색이 2와 4인 것을 모두 고르고 모서리로 연결한 그래프인 <math>G_{2,4}</math>에 대해 생각하자. <math>G_{2,4}</math>가 순환로가 아니라면 <math>G_{1,3}</math>이 순환로가 아닐 때처럼 색을 바꾸면 되는데, <math>G_{2,4}</math>가 순환로라면 ''G''가 평면그래프라는 것에 [[모순]]이다! 따라서 <math>G_{2,4}</math>는 순환로가 아닐 수밖에 없다. 따라서 ''G''를 다섯 가지 색으로 칠할 수 있으므로 언제나 원하는 결론을 얻는다. | :: <math>G_{1,3}</math>에서 ''v''<sub>1</sub>에서 ''v''<sub>3</sub>로 가는 길이 있다고 하자. 그러면 이제 얘 말고 ''G' ''에서 색이 2와 4인 것을 모두 고르고 모서리로 연결한 그래프인 <math>G_{2,4}</math>에 대해 생각하자. <math>G_{2,4}</math>가 순환로가 아니라면 <math>G_{1,3}</math>이 순환로가 아닐 때처럼 색을 바꾸면 되는데, <math>G_{2,4}</math>가 순환로라면 ''G''가 평면그래프라는 것에 [[모순]]이다! 따라서 <math>G_{2,4}</math>는 순환로가 아닐 수밖에 없다. 따라서 ''G''를 다섯 가지 색으로 칠할 수 있으므로 언제나 원하는 결론을 얻는다. | ||
2015년 5월 6일 (수) 11:45 판
진술
오색 정리(Five color theorem)은 임의의 평면그래프를 다섯 가지 색을 이용하여 칠할 수 있다는 명제다. 다시 말해, 평면그래프 G의 색의 개수를 [math]\displaystyle{ \chi(G) }[/math]라 하면,
- [math]\displaystyle{ \chi(G)\le 5 }[/math]
이다.
평면그래프의 색의 개수와 관련해 현재 닝겐 혼자 힘으로 도달할 수 있는 가장 강력한 결론이다.
증명
그래프의 모서리의 수 v에 대한 수학적 귀납법으로 증명하려고 한다.
- 기본 단계: [math]\displaystyle{ v=1 }[/math]이면 평면그래프를 한 가지 색을 이용하여 칠할 수 있다.
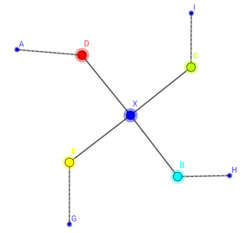
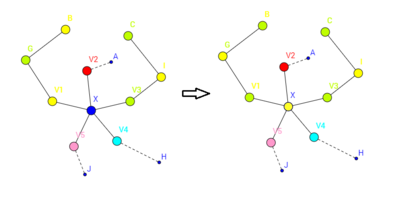
- 귀납법 단계: [math]\displaystyle{ v=n-1 }[/math]인 평면그래프를 다섯 가지 색을 이용하여 칠할 수 있다고 가정하자. [math]\displaystyle{ v=n }[/math]일 때, 평면그래프 G는 차수가 5 이하인 꼭지점을 반드시 하나 가진다.[1] 이 꼭지점을 x라 하자. G에서 x를 제거한 그래프 G' 의 꼭짓점은 n-1개이므로, G' 는 다섯 가지 색을 이용하여 칠할 수 있다. 따라서 G를 다섯 개 색으로 칠할 수 있음을 보이려면 x를 잘 색칠하면 된다.
- [math]\displaystyle{ \deg x \le 4 }[/math]일 때, v와 인접한 꼭짓점의 색은 최대 네 가지에 불과하므로, 인접한 꼭짓점의 색이 아닌 걸 적당히 골라서 x에 색칠하면 된다.
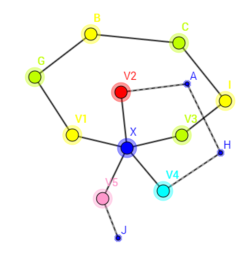
- [math]\displaystyle{ \deg x =5 }[/math]라고 하자. 이때, x와 인접한 꼭짓점을 시계방향으로 [math]\displaystyle{ v_1,v_2,v_3,v_4,v_5 }[/math]로 지정하고, 색을 1, 2, 3, 4, 5로 부여하자. G' 의 부분그래프 [math]\displaystyle{ G_{1,3} }[/math]을 G' 에서 색이 1과 3인 것을 모두 고르고 모서리로 연결한 그래프라고 하자. 이때 [math]\displaystyle{ G_{1,3} }[/math]에서 v1에서 v3로 가는 길이 없다면, v1의 색을 v3의 색으로 바꾸고 v1과 연결된 점의 색 1, 3을 서로 바꾸면 된다. 그리고 x를 1로 칠하면 된다.
- [math]\displaystyle{ G_{1,3} }[/math]에서 v1에서 v3로 가는 길이 있다고 하자. 그러면 이제 얘 말고 G' 에서 색이 2와 4인 것을 모두 고르고 모서리로 연결한 그래프인 [math]\displaystyle{ G_{2,4} }[/math]에 대해 생각하자. [math]\displaystyle{ G_{2,4} }[/math]가 순환로가 아니라면 [math]\displaystyle{ G_{1,3} }[/math]이 순환로가 아닐 때처럼 색을 바꾸면 되는데, [math]\displaystyle{ G_{2,4} }[/math]가 순환로라면 G가 평면그래프라는 것에 모순이다! 따라서 [math]\displaystyle{ G_{2,4} }[/math]는 순환로가 아닐 수밖에 없다. 따라서 G를 다섯 가지 색으로 칠할 수 있으므로 언제나 원하는 결론을 얻는다.
같이 보기
- 사색 정리: 오색 정리보다 강력한 정리로, 임의의 평면그래프는 네 가지 색을 이용해 칠할 수 있다. 1976년에 컴퓨터를 이용해 증명하였다.
외부 링크
- Five Color Theorem. (2014, August 13). ProofWiki, . Retrieved 14:39, May 5, 2015.
각주
- ↑ 박승안 (2012). 『이산수학』(제3판). 경문사. p. 242. ISBN 9788961055345