편집 요약 없음 |
|||
| (사용자 8명의 중간 판 18개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
본격적으로 알고리즘을 종류별로 다룬다. 각 알고리즘을 적용하는 간단한 예시와 연습문제를 제공하니 풀어보면서 이해하는 것이 좋다. 연습문제는 acmicpc.net의 것을 링크한다. [[KOI]] 같은 경시대회를 대비하는데 도움이 될 수도..? | |||
본격적으로 알고리즘을 종류별로 다룬다. 각 알고리즘을 적용하는 간단한 예시와 연습문제를 제공하니 풀어보면서 이해하는 것이 좋다. [[ | |||
== 알고리즘의 정당성 증명 == | == 알고리즘의 정당성 증명 == | ||
갑자기 | 갑자기 웬 뜬금없이 증명이 튀어나왔는지 궁금할 것이다. 당연하지만, 우리는 천재가 아니라서 머릿속으로 생각한 알고리즘이 실제로 아주 잘 돌아간다고 보장할 수 없기 때문에 생각해낸 알고리즘이 문제를 풀 수 있다는 것을 보여야 한다. | ||
=== 수학적 귀납법 === | === 수학적 귀납법 === | ||
다들 수학 공부하면서 한 번씩은 들어봤을 그것이다. 수학적 귀납법을 이용한 증명은 크게 ''단계 나누기''와 ''첫 단계 증명'', ''귀납 증명''으로 나눈다. 자세한 내용은 [[수학적 귀납법|해당 항목]] 참고. | 다들 수학 공부하면서 한 번씩은 들어봤을 그것이다. 수학적 귀납법을 이용한 증명은 크게 ''단계 나누기''와 ''첫 단계 증명'', ''귀납 증명''으로 나눈다. 자세한 내용은 [[수학적 귀납법|해당 항목]] 참고. | ||
| 22번째 줄: | 22번째 줄: | ||
=== 구성적 증명 === | === 구성적 증명 === | ||
위에 언급한 증명 방법들과는 달리, 구성적 증명은 답의 존재성을 보이는 게 아닌, ''답을 구하는 방법 그 자체를 보이는 것''이다. 쉽게 말해, 그냥 '''답을 구하는 알고리즘의 실행 과정을 설명'''한다고 생각하면 된다. | 위에 언급한 증명 방법들과는 달리, 구성적 증명은 답의 존재성을 보이는 게 아닌, ''답을 구하는 방법 그 자체를 보이는 것''이다. 쉽게 말해, 그냥 '''답을 구하는 알고리즘의 실행 과정을 설명'''한다고 생각하면 된다. | ||
== | == 정렬 알고리즘 == | ||
=== 안정 정렬 === | === 안정 정렬 === | ||
비교한 값이 같을 때 서로 바뀌지 않는 정렬법을 안정 정렬이라고 한다. | 비교한 값이 같을 때 서로 바뀌지 않는 정렬법을 안정 정렬이라고 한다. | ||
| 28번째 줄: | 28번째 줄: | ||
==== 거품(Bubble) 정렬 ==== | ==== 거품(Bubble) 정렬 ==== | ||
[[수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초#거품(Bubble) 정렬|해당 항목]] 참고. | [[수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초#거품(Bubble) 정렬|해당 항목]] 참고. | ||
==== 삽입(Insertion) 정렬 ==== | |||
[[수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초#삽입(Insertion) 정렬|해당 항목]] 참고. | |||
==== 병합(Merge) 정렬 ==== | ==== 병합(Merge) 정렬 ==== | ||
분할정복기법의 대표적 예이다. 소스는 은근 쉽다.<!-- 에러 수정바람 --> | 분할정복기법의 대표적 예이다. 소스는 은근 쉽다.<!-- 에러 수정바람 --> | ||
< | <syntaxhighlight lang="C"> | ||
int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9}; | int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9}; | ||
int tmparr[10]; | int tmparr[10]; | ||
| 66번째 줄: | 69번째 줄: | ||
arr[i] = tmparr[i]; | arr[i] = tmparr[i]; | ||
} | } | ||
</ | </syntaxhighlight> | ||
[[파이썬]]에서 재귀 기법을 사용하는 병합 정렬의 예제는 다음과 같다. | [[파이썬]]에서 재귀 기법을 사용하는 병합 정렬의 예제는 다음과 같다. | ||
< | <syntaxhighlight lang="Python"> | ||
def mergeSort(x): | def mergeSort(x): | ||
if len(x) <= 1: | if len(x) <= 1: | ||
| 92번째 줄: | 95번째 줄: | ||
result += R[j:] | result += R[j:] | ||
return result | return result | ||
</ | </syntaxhighlight> | ||
* 연습문제 | |||
*: [https://www.acmicpc.net/problem/1517 버블 소트] | |||
=== 불안정 정렬 === | === 불안정 정렬 === | ||
| 99번째 줄: | 106번째 줄: | ||
==== 선택(Selection) 정렬 ==== | ==== 선택(Selection) 정렬 ==== | ||
[[수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초#선택(Selection) 정렬|해당 항목]] 참고. | [[수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초#선택(Selection) 정렬|해당 항목]] 참고. | ||
==== 퀵(Quick) 정렬 ==== | ==== 퀵(Quick) 정렬 ==== | ||
| 108번째 줄: | 112번째 줄: | ||
예를 들어, 5, 3, 7, 8, 6, 4, 2, 1, 0, 9를 정렬한다고 해보자. 맨 앞의 5를 기준으로 일단 정렬한다. 사람이 한다면 아마 3, 4, 2, 1, 0, '''5''', 7, 8, 6, 9가 될 것이다. 이 상태에서 5의 앞을 다시 정렬한다. 2, 1, 0, '''3''', 4와 '''5'''와 7, 8, 6, 9가 남았다. 이 때, 4는 3 뒤에 있는 오직 한 개의 수이므로 정렬이 되었다고 본다. 이런 식으로 하다 보면 0, 1, 2, 3, 4, 5, 6, 7, 8, 9의 올바른 순열이 나올 것이다. 소스는 다음과 같다.<ref>물론 최적화는 되어 있지 않다.</ref> | 예를 들어, 5, 3, 7, 8, 6, 4, 2, 1, 0, 9를 정렬한다고 해보자. 맨 앞의 5를 기준으로 일단 정렬한다. 사람이 한다면 아마 3, 4, 2, 1, 0, '''5''', 7, 8, 6, 9가 될 것이다. 이 상태에서 5의 앞을 다시 정렬한다. 2, 1, 0, '''3''', 4와 '''5'''와 7, 8, 6, 9가 남았다. 이 때, 4는 3 뒤에 있는 오직 한 개의 수이므로 정렬이 되었다고 본다. 이런 식으로 하다 보면 0, 1, 2, 3, 4, 5, 6, 7, 8, 9의 올바른 순열이 나올 것이다. 소스는 다음과 같다.<ref>물론 최적화는 되어 있지 않다.</ref> | ||
< | <syntaxhighlight lang="C"> | ||
int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9}; | int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9}; | ||
| 147번째 줄: | 151번째 줄: | ||
sort(j + 1, end); | sort(j + 1, end); | ||
} | } | ||
</ | </syntaxhighlight> | ||
[[파이썬]]에서 재귀 기법을 사용하는 퀵 소트 함수의 예제는 다음과 같다. | [[파이썬]]에서 재귀 기법을 사용하는 퀵 소트 함수의 예제는 다음과 같다. | ||
< | <syntaxhighlight lang="Python"> | ||
def quicksort(x): | def quicksort(x): | ||
if len(x) <= 1: | if len(x) <= 1: | ||
| 169번째 줄: | 173번째 줄: | ||
return quicksort(less) + equal + quicksort(more) | return quicksort(less) + equal + quicksort(more) | ||
</ | </syntaxhighlight> | ||
퀵 정렬이 모든 경우에 항상 빠른 것은 아니다. {{ㅊ|거의 항상 빠른 것 뿐이다.}} 최악의 경우, 즉 이미 모든 자료가 | 퀵 정렬이 모든 경우에 항상 빠른 것은 아니다. {{ㅊ|거의 항상 빠른 것 뿐이다.}} 최악의 경우, 즉 이미 모든 자료가 역순으로 정렬된 상태인 경우라면 <math>O(n^2)</math>의 성능을 보일 수 있지만, 정렬 기준을 맨 앞 값 대신 아무거나 하나 골라 잡는 방법으로 해결하면 거의 대부분의 경우에 <math>O(n\log n)</math>의 성능을 보장받을 수 있다. 또한 정렬 기준(초기값, pivot)이 수학적으로 역순으로 정렬된 상태에 절대 잡히지 않도록 정하는 방법도 상당히 많이 제안되어 있어 <math>O(n^2)</math>의 성능이 보일 가능성은 거의 없다. 더불어 실제로 정렬 알고리즘을 돌렸을 때 퀵 정렬은 다른 <math>O(n\log n)</math> 알고리즘보다 캐시 히트 레이트가 높아 훨씬 더 빠르기 때문에 일반적으로 정렬의 대부분은 퀵 정렬 알고리즘을 활용한 형태를 사용한다. | ||
==== 힙(Heap) 정렬 ==== | ==== 힙(Heap) 정렬 ==== | ||
=== 그 밖의 정렬 알고리즘 === | === 그 밖의 정렬 알고리즘 === | ||
==== 버킷( | ==== 버킷(Bucket) 정렬 ==== | ||
==== 자릿수(Radix) 정렬 ==== | ==== 자릿수(Radix) 정렬 ==== | ||
== | == 브루트 포스 == | ||
컴퓨터의 [[크고 아름다운]] 우월한 성능을 이용하여 모든 경우의 수를 시도하는 방법이다. 이 방법을 전문용어로 완전탐색 알고리즘이라고 한다. | 컴퓨터의 [[크고 아름다운]] 우월한 성능을 이용하여 모든 경우의 수를 시도하는 방법이다. 이 방법을 전문용어로 완전탐색 알고리즘이라고 한다. | ||
문제를 쓸데없이 어렵게 접근하여 골치아파하지 말고 이 방법을 가장 먼저 적용하자. 이 방법도 나쁜 방법이 아니며, 준수한 성능을 내는 알고리즘을 설계할 수 있는 좋은 방법이다. | 문제를 쓸데없이 어렵게 접근하여 골치아파하지 말고 이 방법을 가장 먼저 적용하자. 이 방법도 나쁜 방법이 아니며, 준수한 성능을 내는 알고리즘을 설계할 수 있는 좋은 방법이다. | ||
다만 이 방법을 쓰려 한다면,리소스를 많이 써먹을 수 있는 | 다만 이 방법을 쓰려 한다면, 리소스를 많이 써먹을 수 있는 프로그램을 짤 수 있다는 전제조건이 따라붙는다. 크고 아름다운 성능을 이용하려 해도 싱글코어밖에 못 쓰는 프로그램이라면 빛이 바랠 것이다. | ||
=== | == 분할 정복 == | ||
== 동적 계획법 == | |||
프로그래밍 대회에서 가장 사랑받는 알고리즘이다. 정말 별별 문제들이 다 동적 계획법(DP)로 풀린다. 중복되는 계산을 방지하기 위하여 미리 계산값을 저장해두는 표를 만들어두고 계산을 이미 했을 경우 표에서 값을 받아오는 방식이다. 다른 편으로 보자면 속도의 향상을 위하여 메모리를 희생하는 것이다. | |||
=== 재귀적 방법 === | |||
가장 짜기 쉬운 DP의 구현방식이다. 브루트 포스로 짠 뒤에 거기다가 DP Table을 집어넣으면 되는거다. | |||
=== 반복적 방법 === | |||
미리 모든 필요한 데이터들을 DP Table에 채워넣고 거기서 값을 뽑아서 계산하고 출력하는 방식이다. 스택 오버플로우가 날 일이 없어지고, 수행 시간이 줄어들며 토글링을 적용할 수 있다는 장점이 있다. | |||
== 탐욕법 == | |||
그리디 알고리즘 또는 욕심쟁이 알고리즘 등으로도 불리운다. 현재 봤을 때 가장 최적해 같아 보이는 것을 선택하는 알고리즘이다. 근사해를 구할 때 쓰이면 가장 좋으나, 최적해를 구할 때에는 역추적을 해야만 한다. 가장 사람을 잘 흉내내는 알고리즘이다.{{--|이런 욕심쟁이들.}} | |||
== | == 파라매트릭 서치 == | ||
이분법이라고도 한다. 가능한 min, 혹은 max 값을 구하고자 할 때 가능한 정답의 최솟값과 최댓값의 평균에 대해서 이 값에 대해 풀리는지를 계산하고, 후보를 절반씩 줄여나가는 방식이다. | |||
== 계산 기하 == | |||
== 트리 == | == 트리 == | ||
=== 구현과 순회 === | === 구현과 순회 === | ||
=== | === 유니온파인드 트리 === | ||
=== 이진 검색 트리 === | === 이진 검색 트리 === | ||
이진 검색 트리는 고급 자료구조를 위해서 다양하게 활용되기도 한다. 그에 관해서는 다음 문서를 참고. | 이진 검색 트리는 고급 자료구조를 위해서 다양하게 활용되기도 한다. 그에 관해서는 다음 문서를 참고. | ||
| 233번째 줄: | 233번째 줄: | ||
C 코드로 표현하면 다음과 같다. | C 코드로 표현하면 다음과 같다. | ||
< | <syntaxhighlight lang=c> | ||
for(int k = 1; k <= n; ++k) | for(int k = 1; k <= n; ++k) | ||
for(int i = 1; i <= n; ++i) | for(int i = 1; i <= n; ++i) | ||
for(int j = 1; j <= n; ++j) | for(int j = 1; j <= n; ++j) | ||
cost[i][j] = min(cost[i][j], cost[i][k] + cost[k][j]); | cost[i][j] = min(cost[i][j], cost[i][k] + cost[k][j]); | ||
</ | </syntaxhighlight> | ||
이 때, cost[i][j]의 초기값에는 둘을 잇는 간선이 있을 경우 그 간선의 코스트, 없을 경우 무한대에 해당하는 매우 큰 값을 넣는다. | 이 때, cost[i][j]의 초기값에는 둘을 잇는 간선이 있을 경우 그 간선의 코스트, 없을 경우 무한대에 해당하는 매우 큰 값을 넣는다. | ||
* 연습문제 | |||
*: [https://www.acmicpc.net/problem/10159 저울] | |||
==== 데이크스트라(Dijkstra) 알고리즘 ==== | ==== 데이크스트라(Dijkstra) 알고리즘 ==== | ||
{{--|이거 왜 그리디에 없고 여기 있냐}} | {{--|이거 왜 그리디에 없고 여기 있냐}} 유향 그래프에서 간선의 가중치가 모두 음이 아닌 정수일 때, 출발지에서 목적지까지의 최단거리를 찾는 알고리즘이다. 움짤이 여럿 돌아다니니 한 번 보자. | ||
최단거리를 찾는 알고리즘이다. 움짤이 여럿 돌아다니니 한 번 보자. | [[파일:Shortest path Dijkstra vs BellmanFord.gif|thumb|Shortest path Dijkstra vs BellmanFord]] | ||
[[ | |||
{{--|c부터 조사하지 않는 게 수상하긴 하지만 }}윗 것은 데이크스트라, 아랫 것은 벨먼 포드 알고리즘이다. 이것만 보고도 이해할 수 있다면 참 좋겠다. <!-- 다음은 그 소스이다. c로 구현하기 힘든데...--> | {{--|c부터 조사하지 않는 게 수상하긴 하지만 }}윗 것은 데이크스트라, 아랫 것은 벨먼 포드 알고리즘이다. 이것만 보고도 이해할 수 있다면 참 좋겠다. <!-- 다음은 그 소스이다. c로 구현하기 힘든데...--> | ||
| 252번째 줄: | 254번째 줄: | ||
[[추가바람]] | [[추가바람]] | ||
벨먼-포드의 알고리즘은 데이크스트라의 알고리즘과 비슷한 시기에 나왔으나, 데이크스트라의 알고리즘에 비하면 계산 횟수는 더 안 좋지만, 계산 과정과 전달 자체만은 비교적 간결한 형태를 | 벨먼-포드의 알고리즘은 데이크스트라의 알고리즘과 비슷한 시기에 나왔으나, 데이크스트라의 알고리즘에 비하면 계산 횟수는 더 안 좋지만, 계산 과정과 전달 자체만은 비교적 간결한 형태를 띠고 있다. 인터넷에서 라우터가 라우팅을 할 때 사용되는 방법 중 하나인 라우팅 정보 프로토콜(RIP)에서 이 알고리즘을 사용하고 있다. OSPF에 비해서는 비교적 간결한 통신을 하지만, 순환 경로나 수신자가 메시지 도착 전에 가동 불능이 되는 경우에는 문제가 생길 수 있다는 단점이 있다. | ||
=== 위상 정렬 === | === 위상 정렬 === | ||
| 265번째 줄: | 267번째 줄: | ||
=== 강연결요소(SCC) === | === 강연결요소(SCC) === | ||
=== 네트워크 | === 네트워크 플로우 === | ||
==== 포드 펄커슨 알고리즘 ==== | |||
==== 에드몬드 카프 알고리즘 ==== | |||
==== 디닉 알고리즘 ==== | |||
==== 이분 매칭 ==== | |||
==== MCMF ==== | |||
== 문자열 알고리즘 == | == 문자열 알고리즘 == | ||
| 279번째 줄: | 285번째 줄: | ||
접미사 트리에서 필요한 리프노드 부분만 잘라낸 배열인데, 프로그래밍 대회에서 접미사 트리는 잘 안쓰기 때문에 항목명을 바꾸었다. | 접미사 트리에서 필요한 리프노드 부분만 잘라낸 배열인데, 프로그래밍 대회에서 접미사 트리는 잘 안쓰기 때문에 항목명을 바꾸었다. | ||
문자열의 맥가이버 칼이라고 불릴 정도로 정말로 각종 프로그래밍 문제에서 쓰인다. 접미사 배열을 제안한 밴머와 마이어스의 알고리즘을 이용해 <math>O\left( nlg^2n \right)</math><ref><math>O\left( nlgn \right)</math>으로도 구현할 수 있지만, 복잡하고 <math>O\left( nlg^2n \right)</math>으로도 충분해서 안쓴다</ref>의 시간 복잡도로 생성할 수 있다. | 문자열의 맥가이버 칼이라고 불릴 정도로 정말로 각종 프로그래밍 문제에서 쓰인다. 접미사 배열을 제안한 밴머와 마이어스의 알고리즘을 이용해 <math>O\left( nlg^2n \right)</math><ref><math>O\left( nlgn \right)</math>으로도 구현할 수 있지만, 복잡하고 <math>O\left( nlg^2n \right)</math>으로도 충분해서 안쓴다</ref>의 시간 복잡도로 생성할 수 있다. | ||
===== 트라이, 아호 코라식 알고리즘 ===== | |||
KMP의 확장으로, 여러 개의 문자열에 대하여 빠르게 동작할 수 있다. | |||
{{각주}} | |||
[[분류:수학인듯 과학아닌 공학같은 컴퓨터과학]] | [[분류:수학인듯 과학아닌 공학같은 컴퓨터과학]] | ||
[[분류:컴퓨터 과학]] | [[분류:컴퓨터 과학]] | ||
2023년 4월 18일 (화) 19:52 기준 최신판
본격적으로 알고리즘을 종류별로 다룬다. 각 알고리즘을 적용하는 간단한 예시와 연습문제를 제공하니 풀어보면서 이해하는 것이 좋다. 연습문제는 acmicpc.net의 것을 링크한다. KOI 같은 경시대회를 대비하는데 도움이 될 수도..?
알고리즘의 정당성 증명[편집 | 원본 편집]
갑자기 웬 뜬금없이 증명이 튀어나왔는지 궁금할 것이다. 당연하지만, 우리는 천재가 아니라서 머릿속으로 생각한 알고리즘이 실제로 아주 잘 돌아간다고 보장할 수 없기 때문에 생각해낸 알고리즘이 문제를 풀 수 있다는 것을 보여야 한다.
수학적 귀납법[편집 | 원본 편집]
다들 수학 공부하면서 한 번씩은 들어봤을 그것이다. 수학적 귀납법을 이용한 증명은 크게 단계 나누기와 첫 단계 증명, 귀납 증명으로 나눈다. 자세한 내용은 해당 항목 참고.
반복문 불변식[편집 | 원본 편집]
반복문의 내용이 매 번 실행될 때마다 중간 결과가 올바른 답을 도출하기 위한 결과로 잘 나오는지를 판별하는 조건이다. 반복문이 마지막에 올바른 답을 내놓으려면 항상 이 식이 변하지 않아야 한다(그러므로 불변식이라고 한다).
불변식을 이용해 다음과 같이 반복문의 정당성을 증명할 수 있다.
- 반복문 진입시에 불변식이 성립함을 보인다.(초기 조건)
- 반복문 내용이 불변식에 영향을 주지 않음을 보인다.(유지 조건)
- 반복문 종료후 불변식이 성립하면 항상 올바른 답이 나옴을 보인다.
귀류법[편집 | 원본 편집]
수학에서도 많이 사용되는 만능의 증명법, 귀류법이다. 자세한 내용은 해당 항목 참고. 간단히 설명하자면,'이거 부정한다고 생각하고 이렇게 저렇게 해봤어. 근데 부정하면 성립이 안되네? 고로 부정했던 명제가 맞음'쯤 된다.
비둘기집의 원리[편집 | 원본 편집]
경우의 수에서 자주 언급되는 그 원리 맞다. 비둘기집의 원리 참고.
구성적 증명[편집 | 원본 편집]
위에 언급한 증명 방법들과는 달리, 구성적 증명은 답의 존재성을 보이는 게 아닌, 답을 구하는 방법 그 자체를 보이는 것이다. 쉽게 말해, 그냥 답을 구하는 알고리즘의 실행 과정을 설명한다고 생각하면 된다.
정렬 알고리즘[편집 | 원본 편집]
안정 정렬[편집 | 원본 편집]
비교한 값이 같을 때 서로 바뀌지 않는 정렬법을 안정 정렬이라고 한다.
거품(Bubble) 정렬[편집 | 원본 편집]
해당 항목 참고.
삽입(Insertion) 정렬[편집 | 원본 편집]
해당 항목 참고.
병합(Merge) 정렬[편집 | 원본 편집]
분할정복기법의 대표적 예이다. 소스는 은근 쉽다.
int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9};
int tmparr[10];
void sort(int, int);
void merge(int, int);
void sort(int start, int end)
{
if(end > start)
{
sort(start, (start + end) / 2);
sort((start + end) / 2 + 1, end);
}
merge(start, end);
}
void merge(int start, int end) //여기가 진짜다.
{
int i = start, j = (start + end) / 2 + 1;
int count = start;
while(i <= (start + end) / 2 && j <= end)
{
if(arr[i] > arr[j])
tmparr[count++] = arr[j++];
else
tmparr[count++] = arr[i++];
}
while(i <= (start + end) / 2)
tmparr[count++] = arr[i++];
while(j <= end)
tmparr[count++] = arr[j++];
for(i = start; i <= end; i++)
arr[i] = tmparr[i];
}
파이썬에서 재귀 기법을 사용하는 병합 정렬의 예제는 다음과 같다.
def mergeSort(x):
if len(x) <= 1:
return x
m = len(x) // 2
L = mergeSort(x[:m])
R = mergeSort(x[m:])
result = []
i = 0
j = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
result.append(L[i])
i += 1
else:
result.append(R[j])
j += 1
result += L[i:]
result += R[j:]
return result
* 연습문제 *: 버블 소트
불안정 정렬[편집 | 원본 편집]
비교한 값이 같을 때 서로 바뀌는 정렬법을 불안정 정렬이라고 한다.
선택(Selection) 정렬[편집 | 원본 편집]
해당 항목 참고.
퀵(Quick) 정렬[편집 | 원본 편집]
정렬의 왕. 시간 복잡도가 평균 [math]\displaystyle{ O(n\log n) }[/math]인 정렬 알고리즘들 중 가장 빠르다. 자료 중 하나를 정렬 기준으로 잡아서 이 자료보다 작은 걸 왼쪽으로, 큰 걸 오른쪽으로 보내는 걸 반복해 정렬한다고 보면 된다.
예를 들어, 5, 3, 7, 8, 6, 4, 2, 1, 0, 9를 정렬한다고 해보자. 맨 앞의 5를 기준으로 일단 정렬한다. 사람이 한다면 아마 3, 4, 2, 1, 0, 5, 7, 8, 6, 9가 될 것이다. 이 상태에서 5의 앞을 다시 정렬한다. 2, 1, 0, 3, 4와 5와 7, 8, 6, 9가 남았다. 이 때, 4는 3 뒤에 있는 오직 한 개의 수이므로 정렬이 되었다고 본다. 이런 식으로 하다 보면 0, 1, 2, 3, 4, 5, 6, 7, 8, 9의 올바른 순열이 나올 것이다. 소스는 다음과 같다.[1]
int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9};
void sort(int, int);
void sort(int start, int end)
{
int i = start + 1;
int j = end;
if(end < start)
return;
while(i < j)
{
while(arr[i] <= arr[start])
{
i++;
}
while(arr[j] >= arr[start])
{
j--;
}
if(i < j)
{
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
if(arr[start] > arr[j])
{
arr[start] = arr[start] ^ arr[j];
arr[j] = arr[start] ^ arr[j];
arr[start] = arr[start] ^ arr[j];
}
sort(start, j - 1);
sort(j + 1, end);
}
파이썬에서 재귀 기법을 사용하는 퀵 소트 함수의 예제는 다음과 같다.
def quicksort(x):
if len(x) <= 1:
return x
pivot = x[len(x)//2]
less = []
more = []
equal = []
for a in x:
if a < pivot:
less.append(a)
elif a > pivot:
more.append(a)
else:
equal.append(a)
return quicksort(less) + equal + quicksort(more)
퀵 정렬이 모든 경우에 항상 빠른 것은 아니다. 거의 항상 빠른 것 뿐이다. 최악의 경우, 즉 이미 모든 자료가 역순으로 정렬된 상태인 경우라면 [math]\displaystyle{ O(n^2) }[/math]의 성능을 보일 수 있지만, 정렬 기준을 맨 앞 값 대신 아무거나 하나 골라 잡는 방법으로 해결하면 거의 대부분의 경우에 [math]\displaystyle{ O(n\log n) }[/math]의 성능을 보장받을 수 있다. 또한 정렬 기준(초기값, pivot)이 수학적으로 역순으로 정렬된 상태에 절대 잡히지 않도록 정하는 방법도 상당히 많이 제안되어 있어 [math]\displaystyle{ O(n^2) }[/math]의 성능이 보일 가능성은 거의 없다. 더불어 실제로 정렬 알고리즘을 돌렸을 때 퀵 정렬은 다른 [math]\displaystyle{ O(n\log n) }[/math] 알고리즘보다 캐시 히트 레이트가 높아 훨씬 더 빠르기 때문에 일반적으로 정렬의 대부분은 퀵 정렬 알고리즘을 활용한 형태를 사용한다.
힙(Heap) 정렬[편집 | 원본 편집]
그 밖의 정렬 알고리즘[편집 | 원본 편집]
버킷(Bucket) 정렬[편집 | 원본 편집]
자릿수(Radix) 정렬[편집 | 원본 편집]
브루트 포스[편집 | 원본 편집]
컴퓨터의 크고 아름다운 우월한 성능을 이용하여 모든 경우의 수를 시도하는 방법이다. 이 방법을 전문용어로 완전탐색 알고리즘이라고 한다.
문제를 쓸데없이 어렵게 접근하여 골치아파하지 말고 이 방법을 가장 먼저 적용하자. 이 방법도 나쁜 방법이 아니며, 준수한 성능을 내는 알고리즘을 설계할 수 있는 좋은 방법이다.
다만 이 방법을 쓰려 한다면, 리소스를 많이 써먹을 수 있는 프로그램을 짤 수 있다는 전제조건이 따라붙는다. 크고 아름다운 성능을 이용하려 해도 싱글코어밖에 못 쓰는 프로그램이라면 빛이 바랠 것이다.
분할 정복[편집 | 원본 편집]
동적 계획법[편집 | 원본 편집]
프로그래밍 대회에서 가장 사랑받는 알고리즘이다. 정말 별별 문제들이 다 동적 계획법(DP)로 풀린다. 중복되는 계산을 방지하기 위하여 미리 계산값을 저장해두는 표를 만들어두고 계산을 이미 했을 경우 표에서 값을 받아오는 방식이다. 다른 편으로 보자면 속도의 향상을 위하여 메모리를 희생하는 것이다.
재귀적 방법[편집 | 원본 편집]
가장 짜기 쉬운 DP의 구현방식이다. 브루트 포스로 짠 뒤에 거기다가 DP Table을 집어넣으면 되는거다.
반복적 방법[편집 | 원본 편집]
미리 모든 필요한 데이터들을 DP Table에 채워넣고 거기서 값을 뽑아서 계산하고 출력하는 방식이다. 스택 오버플로우가 날 일이 없어지고, 수행 시간이 줄어들며 토글링을 적용할 수 있다는 장점이 있다.
탐욕법[편집 | 원본 편집]
그리디 알고리즘 또는 욕심쟁이 알고리즘 등으로도 불리운다. 현재 봤을 때 가장 최적해 같아 보이는 것을 선택하는 알고리즘이다. 근사해를 구할 때 쓰이면 가장 좋으나, 최적해를 구할 때에는 역추적을 해야만 한다. 가장 사람을 잘 흉내내는 알고리즘이다.이런 욕심쟁이들.
파라매트릭 서치[편집 | 원본 편집]
이분법이라고도 한다. 가능한 min, 혹은 max 값을 구하고자 할 때 가능한 정답의 최솟값과 최댓값의 평균에 대해서 이 값에 대해 풀리는지를 계산하고, 후보를 절반씩 줄여나가는 방식이다.
계산 기하[편집 | 원본 편집]
트리[편집 | 원본 편집]
구현과 순회[편집 | 원본 편집]
유니온파인드 트리[편집 | 원본 편집]
이진 검색 트리[편집 | 원본 편집]
이진 검색 트리는 고급 자료구조를 위해서 다양하게 활용되기도 한다. 그에 관해서는 다음 문서를 참고.
힙[편집 | 원본 편집]
힙은 트리의 일종으로 부모 노드 값이 항상 자식 노드 값보다 큰 트리를 말한다. 힙소트 할 때 쓰는 트리이다. 보통 이진트리로 구현한다. 힙에 새 원소를 넣고 빼는 데에는 [math]\displaystyle{ O(n \log n) }[/math]의 시간 복잡도를 가진다. 뭔가 힙보다 힙정렬이 더 앞에 있는 것 같은 건 눈의 착각이다.
C로 힙을 구현하는 방법은 크게 두 가지, 배열과 포인터가 있다. 포인터로 하는 방법은 직관적이지만 많은 자원(메모리 또는 시간)이 소모된다. 하지만 배열은 힙의 각 노드를 배열의 어떤 인덱스에 대응시킬지 고민해야 하지만 훨씬 자원을 효율적으로 사용할 수 있다.
힙을 이용해 우선순위 큐를 쉽게 구현할 수 있다.
구간 트리[편집 | 원본 편집]
트라이[편집 | 원본 편집]
그래프[편집 | 원본 편집]
최단 경로[편집 | 원본 편집]
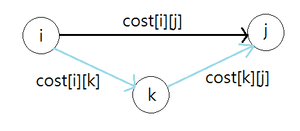
편의상 [math]\displaystyle{ i\longrightarrow j }[/math]로 이동하는 경로의 최소 비용을 [math]\displaystyle{ cost\left[i\right]\left[j\right] }[/math]라고 표기한다.
플로이드-워셜(Floyd-Warshall) 알고리즘[편집 | 원본 편집]
가장 간단하고 이해하기 쉬운 알고리즘이다. 간단하기 때문에 수행 시간도 생각보다 빠른 편이다. 그래프 상에 비용이 음수인 간선이 존재하는 건 괜찮지만 비용이 음수인 사이클이 존재하지 않아야 한다. 모든 정점 쌍들의 최소 비용을 한번에 구해버린다.
현재까지 구한 [math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ j }[/math]로 가는 최소 비용보다 [math]\displaystyle{ i }[/math]에서 [math]\displaystyle{ k }[/math]를 거쳐 [math]\displaystyle{ j }[/math]로 가는 최소비용이 더 작다면 [math]\displaystyle{ cost\left[i\right]\left[j\right] }[/math]를 [math]\displaystyle{ cost\left[i\right]\left[k\right] + cost\left[k\right]\left[j\right] }[/math]로 대치한다. 이렇게 해서 모든 [math]\displaystyle{ \left(i, j\right) }[/math]에 대해 [math]\displaystyle{ cost\left[i\right]\left[j\right] }[/math]를 [math]\displaystyle{ O \left( n^3 \right) }[/math]로 구할 수 있다.
C 코드로 표현하면 다음과 같다.
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
cost[i][j] = min(cost[i][j], cost[i][k] + cost[k][j]);
이 때, cost[i][j]의 초기값에는 둘을 잇는 간선이 있을 경우 그 간선의 코스트, 없을 경우 무한대에 해당하는 매우 큰 값을 넣는다.
* 연습문제 *: 저울
데이크스트라(Dijkstra) 알고리즘[편집 | 원본 편집]
이거 왜 그리디에 없고 여기 있냐 유향 그래프에서 간선의 가중치가 모두 음이 아닌 정수일 때, 출발지에서 목적지까지의 최단거리를 찾는 알고리즘이다. 움짤이 여럿 돌아다니니 한 번 보자.
c부터 조사하지 않는 게 수상하긴 하지만 윗 것은 데이크스트라, 아랫 것은 벨먼 포드 알고리즘이다. 이것만 보고도 이해할 수 있다면 참 좋겠다.
데이크스트라의 알고리즘은 인터넷의 네크워크 계층에서 라우터가 라우팅을 할 때 사용되는 방법 중 하나로 최단 경로 우선 프로토콜(OSPF)에 사용된다.
벨먼-포드(Bellman-Ford) 알고리즘[편집 | 원본 편집]
벨먼-포드의 알고리즘은 데이크스트라의 알고리즘과 비슷한 시기에 나왔으나, 데이크스트라의 알고리즘에 비하면 계산 횟수는 더 안 좋지만, 계산 과정과 전달 자체만은 비교적 간결한 형태를 띠고 있다. 인터넷에서 라우터가 라우팅을 할 때 사용되는 방법 중 하나인 라우팅 정보 프로토콜(RIP)에서 이 알고리즘을 사용하고 있다. OSPF에 비해서는 비교적 간결한 통신을 하지만, 순환 경로나 수신자가 메시지 도착 전에 가동 불능이 되는 경우에는 문제가 생길 수 있다는 단점이 있다.
위상 정렬[편집 | 원본 편집]
DAG에서 모든 노드에 대해서 자신을 가르키는 노드가 무조건 자신의 앞에 오도록 순서를 매기는 것이다.
최소 비용 스패닝 트리(MST)[편집 | 원본 편집]
크러스컬(Kruskal) 알고리즘[편집 | 원본 편집]
가중치가 있는 양방향 그래프(무향 그래프)에서 최단 거리를 찾을 때 사용하는 그리디 알고리즘이다. 사이클이 있는 그래프에서 가중치가 높은 간선을 쳐내는 방식으로 진행하며, 간선을 전부 정리하면 최소 신장 트리(MST)가 된다.
프림(Prim) 알고리즘[편집 | 원본 편집]
강연결요소(SCC)[편집 | 원본 편집]
네트워크 플로우[편집 | 원본 편집]
포드 펄커슨 알고리즘[편집 | 원본 편집]
에드몬드 카프 알고리즘[편집 | 원본 편집]
디닉 알고리즘[편집 | 원본 편집]
이분 매칭[편집 | 원본 편집]
MCMF[편집 | 원본 편집]
문자열 알고리즘[편집 | 원본 편집]
문자열 검색[편집 | 원본 편집]
KMP 알고리즘[편집 | 원본 편집]
카누스-모리스-프렛 3명이 개발한 알고리즘이다. 부분 일치 표를 시드 문자열에서 전처리하고 그에 따라 문자열이 시드와 일치하지 않을 경우 부분 일치 표에서 참조하여 일정 부분은 확인하지 않고도 같지 않다고 확신할 수 있다는 알고리즘이다. 부분 일치 표는 KMP 알고리즘을 재활용하여 생성할 수 있다. [math]\displaystyle{ O\left( m+n \right) }[/math]의 시간복잡도를 항상 제공하며, 이해하기는 어렵지만 이해하면 상당히 많은 곳에 써먹을 수 있는 알고리즘이다.
보이어-무어 알고리즘[편집 | 원본 편집]
일종의 '실패 함수'를 이용해서 구현되는 알고리즘. 평소에는 KMP를 능가하는 속도를 가지고 있지만 특수한 경우에 나이브한 알고리즘보다도 느리기 때문에 프로그래밍 대회에서는 버림받는다.
최종병기 접미사 배열[편집 | 원본 편집]
접미사 트리에서 필요한 리프노드 부분만 잘라낸 배열인데, 프로그래밍 대회에서 접미사 트리는 잘 안쓰기 때문에 항목명을 바꾸었다. 문자열의 맥가이버 칼이라고 불릴 정도로 정말로 각종 프로그래밍 문제에서 쓰인다. 접미사 배열을 제안한 밴머와 마이어스의 알고리즘을 이용해 [math]\displaystyle{ O\left( nlg^2n \right) }[/math][2]의 시간 복잡도로 생성할 수 있다.
트라이, 아호 코라식 알고리즘[편집 | 원본 편집]
KMP의 확장으로, 여러 개의 문자열에 대하여 빠르게 동작할 수 있다.