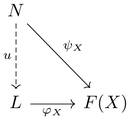범주론에서, 극한은 (category의 object들의) 곱, 당김(pullback), 역극한(inverse limit) 등의 공통적인 보편 성질(universal property)을 말하기 위해 만들어진 개념이다. 범주론적 극한은 위상적인 극한을 포함한다. 즉, 위상적인 극한은 범주론적 극한의 특수한 경우이다.
정의
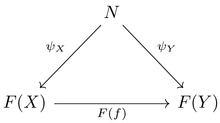
극한의 정의는 universal cone, 즉 보편 성질을 만족하는 뿔이다. [math]\displaystyle{ J }[/math]-형의 [math]\displaystyle{ \mathcal C }[/math]의 다이어그램(공변 함자) [math]\displaystyle{ F: \; J \to \mathcal C }[/math]의 뿔 [math]\displaystyle{ (N, \psi) }[/math]이란 [math]\displaystyle{ J }[/math]의 임의의 대상 [math]\displaystyle{ X, Y }[/math]에 대하여 다음이 가환이게 하는 [math]\displaystyle{ \mathcal C }[/math]의 대상 [math]\displaystyle{ N }[/math]과 함수족 [math]\displaystyle{ \psi_\bullet }[/math]의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 쌍이다:
그러한 뿔 중, 다음과 같은 보편 성질을 가지는 [math]\displaystyle{ (L, \varphi) }[/math]를 다이어그램 [math]\displaystyle{ F }[/math]의 극한이라고 한다:
- 주어진 다이어그램의 임의의 뿔 [math]\displaystyle{ (N, \psi) }[/math]에 대하여,
- [math]\displaystyle{ N, L, F(X) }[/math] (F(X)는 주어진 다이어그램의 object)
- 로 이루어진 아래 다이어그램을 가환하게 하는 사상 [math]\displaystyle{ u: \; N \to L }[/math](factorization)이 유일하게 존재한다.
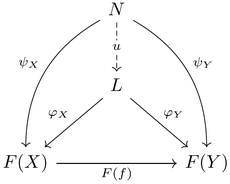
즉, 다음을 가환하게 하는 [math]\displaystyle{ (L, \varphi) }[/math]이다. (이는 [math]\displaystyle{ (L, \varphi) }[/math]과 [math]\displaystyle{ (N, \psi) }[/math]이 cone임에서 나온다.)
기존의 극한 개념으로 봤을 때 참으로 뜬금없는 정의인데, 왜 이름은 극한인 것인가? 그리고 이 개념을 정의한 이유는 무엇인가? 이는 많은 수의 범주론적 개념이 극한으로 일반화되기 때문이며, 범주론에서 가장 중요한 성질인 보편 성질을 capture하기 때문이다.
자연 동형을 이용한 정의
이를 자연 동형(natural isomorphism)의 언어로 나타낼 수도 있다. 먼저, 뿔이란 꼭짓점에서 다이어그램으로 가는 자연 변환이라고 볼 수 있다. [math]\displaystyle{ J }[/math]-형의 [math]\displaystyle{ \mathcal C }[/math]의 다이어그램 [math]\displaystyle{ F : \; J \to \mathcal C }[/math]에 대하여, 꼭짓점 [math]\displaystyle{ V }[/math]에서 내린 뿔은 자연 변환 [math]\displaystyle{ \psi: \; \Delta_ V \to F }[/math]이다. 이때, [math]\displaystyle{ \Delta_V }[/math]는 [math]\displaystyle{ J }[/math]-형의 terminal category [math]\displaystyle{ V }[/math]⟲[math]\displaystyle{ 1_V }[/math]의 다이어그램이다.
이제 위의 자연 동형의 언어로 쓰여진 뿔을 이용하여 극한 역시 자연 동형으로 기술할 수 있다. 즉 다이어그램 [math]\displaystyle{ F }[/math]의 극한은 보편 성질을 만족하는 자연 변환 [math]\displaystyle{ \varphi: \; \Delta_L \to F }[/math]을 말한다.
예시
- 끝 대상: [math]\displaystyle{ J = \mathbf 0 }[/math]가 empty category일 때, [math]\displaystyle{ \mathbf 0 }[/math]-형의 [math]\displaystyle{ \mathcal C }[/math]의 다이어그램은 자명하게 유일하며 이의 극한은 다름아닌 [math]\displaystyle{ \mathcal C }[/math]의 terminal object [math]\displaystyle{ 1 }[/math]이다.
- 곱: [math]\displaystyle{ J }[/math]가 discrete category일 때, 다이어그램 [math]\displaystyle{ F: \; J \to \mathcal C }[/math]는 [math]\displaystyle{ \{X_\alpha \in \operatorname{ob} \mathcal C: \; \alpha \in J \} }[/math]와 같은 의미를 가지게 된다. 이때, 극한의 함수족 [math]\displaystyle{ \varphi_\bullet }[/math]이 projection mapping의 역할을 하게 되어 주어진 다이어그램의 극한은 범주론적 곱이 된다.
- 멱범주: [math]\displaystyle{ F }[/math]가 같은 것 [math]\displaystyle{ X }[/math]만 가리키는 함자이면, 즉 상수 다이어그램이면, 그 극한은 같은 대상을 여러 번 곱하는 것이므로 멱범주 [math]\displaystyle{ X^J }[/math]가 된다.
- 이퀄라이저 (커널): 만약 [math]\displaystyle{ J= \{ \bullet\rightrightarrows \bullet \} }[/math]이면 다이어그램은 평행한(domain과 codomain이 같은) 두 morphism의 쌍을 나타낸다. 이때 그 극한은 두 morphism의 equalizer가 된다.
- 당김: [math]\displaystyle{ J= \{ \bullet\rightarrow \bullet \leftarrow \bullet \} }[/math]이고 [math]\displaystyle{ F }[/math]가 왼쪽의 [math]\displaystyle{ \bullet }[/math]들을 [math]\displaystyle{ X, Z, Y \in \operatorname{ob}\mathcal C }[/math]의 순서로 지정하는 다이어그램이라고 하자. 이때 [math]\displaystyle{ F }[/math]의 극한은 당김(pullback, fibre product라고도 부름)이 된다.
- 역극한: [math]\displaystyle{ J }[/math]를 반순서집합이라고 하고 이것을 범주로 간주하자. (반순서집합은 [math]\displaystyle{ x \le y }[/math]일 때 [math]\displaystyle{ x \to y }[/math]의 morphism을 만드는 방식으로 범주로 생각할 수 있다.) 이때 다이어그램 [math]\displaystyle{ F:\; J^{\mathrm{op}} \to \mathcal C }[/math]을 생각하면, ([math]\displaystyle{ J \to \mathcal C }[/math]의 반변 함자인 [math]\displaystyle{ F }[/math]에 대하여) [math]\displaystyle{ F }[/math]의 극한을 역극한이라고 한다.
- [math]\displaystyle{ J = \mathbf 1 = \{ \lt math\gt \bullet }[/math]⟲[math]\displaystyle{ 1_\bullet \} }[/math]이면, 다이어그램은 단지 [math]\displaystyle{ \mathcal C }[/math]의 한 object [math]\displaystyle{ X }[/math]를 가리키는 함자가 된다. 따라서 vertex [math]\displaystyle{ N }[/math]의 뿔은 [math]\displaystyle{ N \to X=F(\bullet) }[/math]의 morphism과 같고, 이 morphism이 isomorphism일 때에만 주어진 뿔이 극한이 됨을 알 수 있다. 일반적으로 [math]\displaystyle{ J }[/math]가 initial object[math]\displaystyle{ 0 }[/math]을 가지는 범주이면, 임의의 다이어그램 [math]\displaystyle{ F }[/math]는 '[math]\displaystyle{ F(0) }[/math]과 isomorphic한 대상'이라는 극한을 가진다.
성질
해석학과 위상수학의 극한과의 관계
위상공간 [math]\displaystyle{ (X,\mathcal T) }[/math]이 주어져 있다고 하자. [math]\displaystyle{ \mathcal F(X) }[/math]를 X의 필터들의 ⊆-반순서집합이라고 하고, 작은 범주로 간주하자.
[math]\displaystyle{ x\in X }[/math]와 [math]\displaystyle{ F\in\mathcal F(X) }[/math]가 주어져 있을 때 [math]\displaystyle{ \mathcal U_X(x) }[/math]를 [math]\displaystyle{ x }[/math]의 근방 필터(근방들을 모두 모아 놓은 필터)라고 하고, [math]\displaystyle{ \mathcal F_{x,F} (X) }[/math]를
- [math]\displaystyle{ \{G\in\mathcal F(X):\; F\cup\mathcal U_X(x)\subseteq G\} }[/math]
가 생성하는 [math]\displaystyle{ \mathcal F(X) }[/math]의 충만한 부분범주(포함 함자가 충만한 부분범주)라고 하자.
[math]\displaystyle{ E:\mathcal F_{x,F}\hookrightarrow\mathcal F(X) }[/math]는 자명한 충실한 다이어그램이고, [math]\displaystyle{ \Delta }[/math]는 대각 함자이며 [math]\displaystyle{ \lambda:\; \Delta(F)\Rightarrow E }[/math]는 [math]\displaystyle{ G\in\mathcal F_{x,F} }[/math]에 대하여 [math]\displaystyle{ \lambda(G):\; F\hookrightarrow G }[/math]가 포함 함자가 되게 하는 자연 변환이다.
그러면 [math]\displaystyle{ F }[/math]가 [math]\displaystyle{ (X, \mathcal T) }[/math]에서 [math]\displaystyle{ x }[/math]로 수렴(필터가 주어진 점의 근방 필터를 부분 집합으로 포함)하는 것과 자연 변환 [math]\displaystyle{ \lambda }[/math]가 다이어그램 [math]\displaystyle{ E }[/math]의 극한인 것이 동치이다. [1]