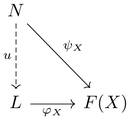잔글 (→정의) |
잔글편집 요약 없음 |
||
| 2번째 줄: | 2번째 줄: | ||
==정의== | ==정의== | ||
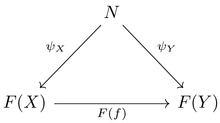
극한의 정의는 '''universal cone''', 즉 보편 성질을 만족하는 [[뿔 (범주론)|뿔]]이다. [[다이어그램]]([[공변 함자]]) <math>F: \; J \to \mathcal C</math>의 '''뿔''' <math>(N, \psi)</math>이란 <math>J</math>의 임의의 [[대상 (수학)|대상]] <math>X, Y</math>에 대하여 다음이 가환이게 하는 <math>\mathcal C</math>의 대상 <math>N</math>과 함수족 <math>\psi_\bullter</math>의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 쌍이다: | 극한의 정의는 '''universal cone''', 즉 보편 성질을 만족하는 [[뿔 (범주론)|뿔]]이다. <math>J</math>-형의 <math>\mathcal C</math>의 [[다이어그램]]([[공변 함자]]) <math>F: \; J \to \mathcal C</math>의 '''뿔''' <math>(N, \psi)</math>이란 <math>J</math>의 임의의 [[대상 (수학)|대상]] <math>X, Y</math>에 대하여 다음이 가환이게 하는 <math>\mathcal C</math>의 대상 <math>N</math>과 함수족 <math>\psi_\bullter</math>의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 쌍이다: | ||
<div align=center>[[파일:cone.png|220px]]</div> | <div align=center>[[파일:cone.png|220px]]</div> | ||
| 21번째 줄: | 21번째 줄: | ||
== 범주론적 구조와 그 공통성, 보편 성질 == | == 범주론적 구조와 그 공통성, 보편 성질 == | ||
{{참조|보편 성질}} | |||
== 예시 == | |||
* [[끝 대상]]: If J is the empty category there is only one diagram of type J: the empty one (similar to the empty function in set theory). A cone to the empty diagram is essentially just an object of C. The limit of F is any object that is uniquely factored through by every other object. This is just the definition of a terminal object. | |||
* [[곱 (범주론)|곱]] If J is a discrete category then a diagram F is essentially nothing but a family of objects of C, indexed by J. The limit L of F is called the product of these objects. The cone φ consists of a family of morphisms φX : L → F(X) called the projections of the product. In the category of sets, for instance, the products are given by Cartesian products and the projections are just the natural projections onto the various factors. | |||
** 멱범주: A special case of a product is when the diagram F is a constant functor to an object X of C. The limit of this diagram is called the Jth power of X and denoted X^J. | |||
*이퀄라이저(커널): If J is a category with two objects and two parallel morphisms from object 1 to object 2 then a diagram of type J is a pair of parallel morphisms in C. The limit L of such a diagram is called an equalizer of those morphisms. | |||
* [[당김]]: Let F be a diagram that picks out three objects X, Y, and Z in C, where the only non-identity morphisms are f : X → Z and g : Y → Z. The limit L of F is called a pullback or a fiber product. It can nicely be visualized as a commutative square: | |||
* [[역극한]]: Let J be a directed poset (considered as a small category by adding arrows i → j if and only if i ≤ j) and let F : Jop → C be a diagram. The limit of F is called (confusingly) an inverse limit or projective limit. | |||
If J = 1, the category with a single object and morphism, then a diagram of type J is essentially just an object X of C. A cone to an object X is just a morphism with codomain X. A morphism f : Y → X is a limit of the diagram X if and only if f is an isomorphism. More generally, if J is any category with an initial object i, then any diagram of type J has a limit, namely any object isomorphic to F(i). Such an isomorphism uniquely determines a universal cone to F. | |||
2016년 12월 6일 (화) 09:41 판
범주론에서, 극한은 (category의 object들의) 곱, 당김(pullback), 역극한(inverse limit) 등의 공통적인 보편 성질(universal property)을 말하기 위해 만들어진 개념이다. 범주론적 극한은 위상적인 극한을 포함한다. 즉, 위상적인 극한은 범주론적 극한의 특수한 경우이다.
정의
극한의 정의는 universal cone, 즉 보편 성질을 만족하는 뿔이다. [math]\displaystyle{ J }[/math]-형의 [math]\displaystyle{ \mathcal C }[/math]의 다이어그램(공변 함자) [math]\displaystyle{ F: \; J \to \mathcal C }[/math]의 뿔 [math]\displaystyle{ (N, \psi) }[/math]이란 [math]\displaystyle{ J }[/math]의 임의의 대상 [math]\displaystyle{ X, Y }[/math]에 대하여 다음이 가환이게 하는 [math]\displaystyle{ \mathcal C }[/math]의 대상 [math]\displaystyle{ N }[/math]과 함수족 [math]\displaystyle{ \psi_\bullter }[/math]의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 쌍이다:
그러한 뿔 중, 다음과 같은 보편 성질을 가지는 [math]\displaystyle{ (L, \varphi) }[/math]를 다이어그램 [math]\displaystyle{ F }[/math]의 극한이라고 한다:
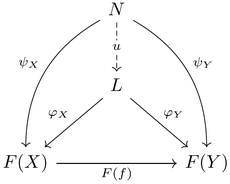
- 주어진 다이어그램의 임의의 뿔 [math]\displaystyle{ (N, \psi) }[/math]에 대하여, [math]\displaystyle{ N, L, F(X) }[/math] (F(X)는 주어진 다이어그램의 object)로 이루어진 아래 다이어그램을 가환하게 하는 사상 [math]\displaystyle{ u: \; N \to L }[/math](factorization)이 유일하게 존재한다.
즉, 다음을 가환하게 하는 [math]\displaystyle{ (L, \varphi) }[/math]이다. (이는 [math]\displaystyle{ (L, \varphi) }[/math]과 [math]\displaystyle{ (N, \psi) }[/math]이 cone임에서 나온다.)
기존의 극한 개념으로 봤을 때 참으로 뜬금없는 정의인데, 왜 이름은 극한인 것인가? 그리고 이 개념을 정의한 이유는 무엇인가?
범주론적 구조와 그 공통성, 보편 성질
예시
- 끝 대상: If J is the empty category there is only one diagram of type J: the empty one (similar to the empty function in set theory). A cone to the empty diagram is essentially just an object of C. The limit of F is any object that is uniquely factored through by every other object. This is just the definition of a terminal object.
- 곱 If J is a discrete category then a diagram F is essentially nothing but a family of objects of C, indexed by J. The limit L of F is called the product of these objects. The cone φ consists of a family of morphisms φX : L → F(X) called the projections of the product. In the category of sets, for instance, the products are given by Cartesian products and the projections are just the natural projections onto the various factors.
- 멱범주: A special case of a product is when the diagram F is a constant functor to an object X of C. The limit of this diagram is called the Jth power of X and denoted X^J.
- 이퀄라이저(커널): If J is a category with two objects and two parallel morphisms from object 1 to object 2 then a diagram of type J is a pair of parallel morphisms in C. The limit L of such a diagram is called an equalizer of those morphisms.
- 당김: Let F be a diagram that picks out three objects X, Y, and Z in C, where the only non-identity morphisms are f : X → Z and g : Y → Z. The limit L of F is called a pullback or a fiber product. It can nicely be visualized as a commutative square:
- 역극한: Let J be a directed poset (considered as a small category by adding arrows i → j if and only if i ≤ j) and let F : Jop → C be a diagram. The limit of F is called (confusingly) an inverse limit or projective limit.
If J = 1, the category with a single object and morphism, then a diagram of type J is essentially just an object X of C. A cone to an object X is just a morphism with codomain X. A morphism f : Y → X is a limit of the diagram X if and only if f is an isomorphism. More generally, if J is any category with an initial object i, then any diagram of type J has a limit, namely any object isomorphic to F(i). Such an isomorphism uniquely determines a universal cone to F.
성질
해석학과 위상수학의 극한과의 관계
위상공간 [math]\displaystyle{ (X,\mathcal O) }[/math]이 주어져 있다고 하자. [math]\displaystyle{ \mathcal F(X) }[/math]를 X의 필터들의 ⊆-반순서집합이라고 하고, 작은 범주로 간주하자. [math]\displaystyle{ x\in X }[/math]와 [math]\displaystyle{ F\in\mathcal F(X) }[/math]가 주어져 있을 때 [math]\displaystyle{ \mathcal U_X(x) }[/math]를 [math]\displaystyle{ x }[/math]의 근방 필터라고 하고, [math]\displaystyle{ \mathcal F_{x,F}^f(X) }[/math]를 [math]\displaystyle{ \{G\in\mathcal F(X):\; F\cup\mathcal U_X(x)\subseteq G\} }[/math]가 생성하는 [math]\displaystyle{ \mathcal F(X) }[/math]의 충만한 부분범주(포함 함자가 충만한 부분범주)라고 하자. [math]\displaystyle{ E:\mathcal F_{x,F}^f\hookrightarrow\mathcal F(X) }[/math]는 자명한 충실한 다이어그램이고, [math]\displaystyle{ \Delta }[/math]는 대각 함자이며 [math]\displaystyle{ \lambda:\; \Delta(F)\Rightarrow E }[/math]는 [math]\displaystyle{ G\in\mathcal F_{x,F}^f }[/math]에 대하여 [math]\displaystyle{ \lambda(G):\; F\hookrightarrow G }[/math]가 포함 함자가 되게 하는 자연 변환이다. 그러면 [math]\displaystyle{ F }[/math]가 [math]\displaystyle{ (X, \mathcal O) }[/math]에서 [math]\displaystyle{ x }[/math]로 수렴하는 것과 [math]\displaystyle{ \lambda }[/math]가 다이어그램 [math]\displaystyle{ E }[/math]의 극한인 것이 동치이다. [1]