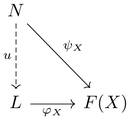잔글편집 요약 없음 |
잔글편집 요약 없음 |
||
| 3번째 줄: | 3번째 줄: | ||
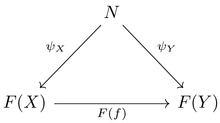
극한의 정의는 '''universal cone''', 즉 보편 성질을 만족하는 [[뿔 (범주론)|뿔]]이다. 다이어그램 <math>F: \; J \to \mathcal C</math>의 '''뿔''' <math>(N, \psi)</math>이란 <math>J</math>의 임의의 대상 <math>X, Y</math>에 대하여 다음이 가환이게 하는 대상과 함수족의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 것이다: | 극한의 정의는 '''universal cone''', 즉 보편 성질을 만족하는 [[뿔 (범주론)|뿔]]이다. 다이어그램 <math>F: \; J \to \mathcal C</math>의 '''뿔''' <math>(N, \psi)</math>이란 <math>J</math>의 임의의 대상 <math>X, Y</math>에 대하여 다음이 가환이게 하는 대상과 함수족의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 것이다: | ||
<div align=center>[[파일:cone.png| | <div align=center>[[파일:cone.png|220px]]</div> | ||
그러한 뿔 중, 다음과 같은 보편 성질을 가지는 <math>(L, \varphi)</math>를 다이어그램(covariant functor) <math>F</math>의 '''극한'''이라고 한다: | 그러한 뿔 중, 다음과 같은 보편 성질을 가지는 <math>(L, \varphi)</math>를 다이어그램(covariant functor) <math>F</math>의 '''극한'''이라고 한다: | ||
| 9번째 줄: | 9번째 줄: | ||
<div align=center> | <div align=center> | ||
[[파일:F-cone.png| | [[파일:F-cone.png|130px|Cone]] | ||
</div> | </div> | ||
| 15번째 줄: | 15번째 줄: | ||
<div align=center> | <div align=center> | ||
[[파일:Commutative Diagram for Categorical Limit.png| | [[파일:Commutative Diagram for Categorical Limit.png|230px|Commutative diagram for Categorical Limit]] | ||
</div> | </div> | ||
2016년 12월 6일 (화) 01:22 판
범주론적 극한
범주론에서, 극한은 (category의 object들의) 곱, 당김(pullback), 역극한(inverse limit) 등의 공통적인 보편 성질(universal property)을 말하기 위해 만들어진 개념이다. 범주론적 극한은 위상적인 극한을 포함한다. 즉, 위상적인 극한은 범주론적 극한의 특수한 경우이다.
극한의 정의는 universal cone, 즉 보편 성질을 만족하는 뿔이다. 다이어그램 [math]\displaystyle{ F: \; J \to \mathcal C }[/math]의 뿔 [math]\displaystyle{ (N, \psi) }[/math]이란 [math]\displaystyle{ J }[/math]의 임의의 대상 [math]\displaystyle{ X, Y }[/math]에 대하여 다음이 가환이게 하는 대상과 함수족의 쌍이다. 즉, 그려지는 모든 삼각형이 가환이게 하는 것이다:
그러한 뿔 중, 다음과 같은 보편 성질을 가지는 [math]\displaystyle{ (L, \varphi) }[/math]를 다이어그램(covariant functor) [math]\displaystyle{ F }[/math]의 극한이라고 한다:
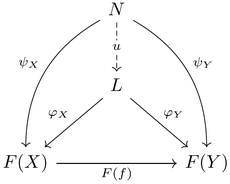
- 주어진 다이어그램의 임의의 뿔 [math]\displaystyle{ (N, \psi) }[/math]에 대하여, [math]\displaystyle{ N, L, F(X) }[/math] (F(X)는 주어진 다이어그램의 object)로 이루어진 아래 다이어그램을 가환하게 하는 사상 [math]\displaystyle{ u: \; N \to L }[/math](factorization)이 유일하게 존재한다.
즉, 다음을 가환하게 하는 [math]\displaystyle{ (L, \varphi) }[/math]이다. (이는 [math]\displaystyle{ (L, \varphi) }[/math]과 [math]\displaystyle{ (N, \psi) }[/math]이 cone임에서 나온다.)
기존의 극한 개념으로 봤을 때 참으로 뜬금없는 정의인데, 왜 이름은 극한인 것인가? 그리고 이 개념을 정의한 이유는 무엇인가?
해석학과 위상수학의 극한과의 관계
Let [math]\displaystyle{ (X,\mathcal O) }[/math] be a topological space, [math]\displaystyle{ \mathcal F(X) }[/math] the partialy ordered set of filters on [math]\displaystyle{ X }[/math] with respect to inclusions, considered as a small category in the usual way. Given [math]\displaystyle{ x\in X }[/math] and [math]\displaystyle{ F\in\mathcal F(X) }[/math] let [math]\displaystyle{ \mathcal U_X(x) }[/math] denote the neighbourhood filter of [math]\displaystyle{ x }[/math] in [math]\displaystyle{ (X,\mathcal O) }[/math] and [math]\displaystyle{ \mathcal F_{x,F}(X) }[/math] the full subcategory of [math]\displaystyle{ \mathcal F(X) }[/math] generated by [math]\displaystyle{ \{G\in\mathcal F(X):F\cup\mathcal U_X(x)\subseteq G\} }[/math], let [math]\displaystyle{ E:\mathcal F_{x,F}\hookrightarrow\mathcal F(X) }[/math] be the obvious (embedding) diagram, [math]\displaystyle{ \Delta }[/math] the usual diagonal functor and [math]\displaystyle{ \lambda:\Delta(F)\rightarrow E }[/math] the natural transformation where [math]\displaystyle{ \lambda(G):F\hookrightarrow G }[/math] is the inclusion for each [math]\displaystyle{ G\in\mathcal F_{x,F} }[/math]. It is not hard to see that [math]\displaystyle{ F }[/math] tends to [math]\displaystyle{ x }[/math] in [math]\displaystyle{ (X,\mathcal O) }[/math] iff [math]\displaystyle{ \lambda }[/math] is a limit of [math]\displaystyle{ E }[/math]. [1]