동적 계획법

Dynamic Programming, DP.

개요

동적 계획법은 어떤 최적화 문제를, 작은 부분 문제로 나누어 차례대로 해결하는 알고리즘을 말한다.

이름이 Dynamic Programming이지만 그닥 역동적인 알고리즘은 아닌데, 예산을 따오기 위해 멋진 이름을 지었다고 카더라(...). 또한 Programming은 컴퓨터 프로그래밍을 의미하는 것이 아니고, 선형계획법처럼 최적화 문제의 해결 방법이라는 의미이다.

예시

그냥 이론을 설명하기에는 복잡하니, 예시를 보며 이해해 보자.

피보나치 수열 구하기

피보나치 수열은 제 0항을 0, 제 1항을 1로 하고, 그 다음 항부터는 이전 두 개 항의 합으로 나타나는 수열이다.

이를 점화식으로 표현하면 [math]\displaystyle{ \mathrm{fib}(n) = \mathrm{fib}(n - 1) + \mathrm{fib}(n - 2) (n \gt 2), \mathrm{fib}(0) = 0, \mathrm{fib}(1) = 1 }[/math]가 된다.

이를 계산하는 프로그램을 작성해 보자. 점화식에 충실하게 재귀함수로 풀면 다음과 같을 것이다.

def fib(n):
    if n == 1 or n == 0:
        return n
    return fib(n - 1) + fib(n - 2)

분명 잘 작동하긴 하는데, 문제는 숫자가 조금만 커져도 시간이 너무 오래 걸린다는 점이다. [math]\displaystyle{ \mathrm{fib}(5) }[/math]의 계산 과정을 그림으로 그려보면 다음과 같다.

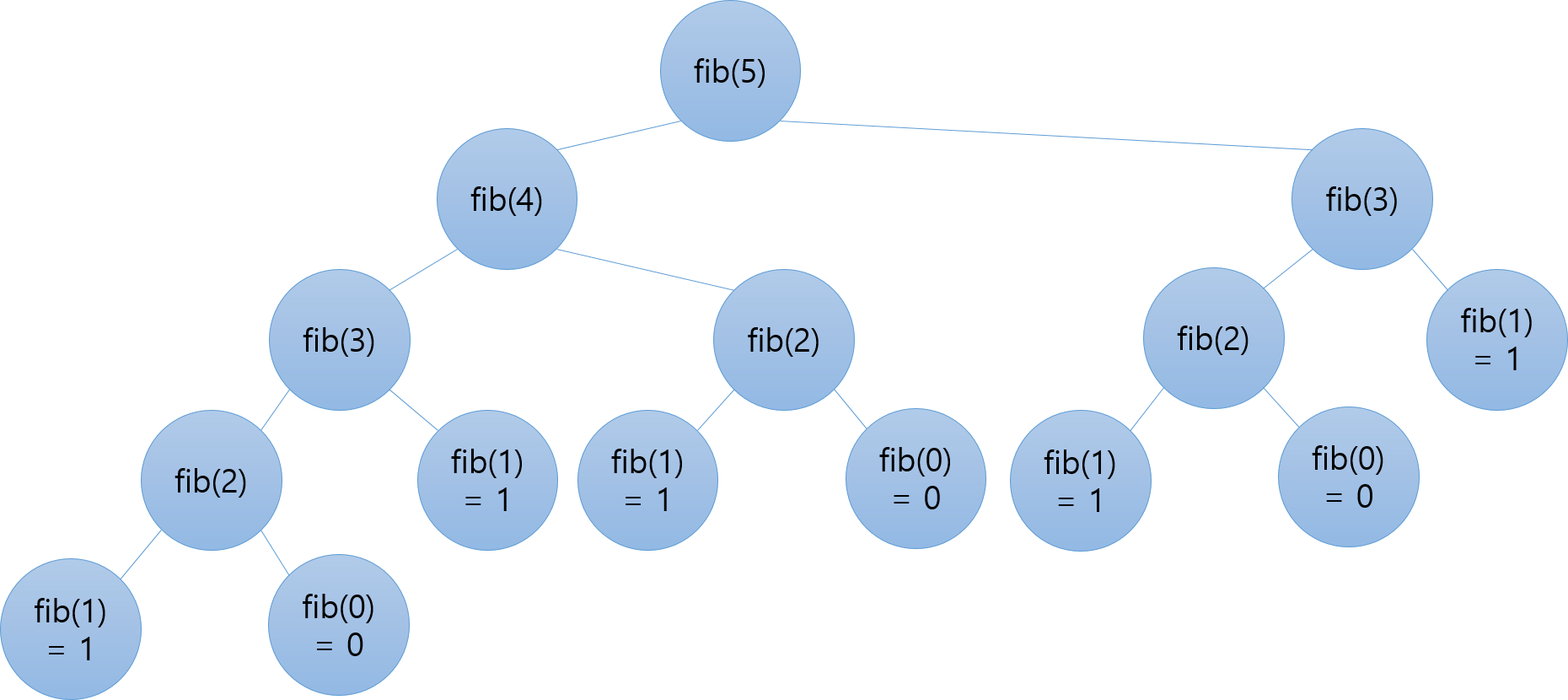
위의 동그라미는 아래 두 개의 동그라미의 합으로 채워진다. 얼마나 많은 계산이 필요한지 알 수 있다. 그런데 저 계산들 중 중복되는 것이 보이지 않는가?

저 과정에서 [math]\displaystyle{ \mathrm{fib}(2) }[/math]는 3번, [math]\displaystyle{ \mathrm{fib}(3) }[/math]는 2번 계산됨을 알 수 있다. 이걸 일일히 계산하지 말고, 한번 구한 값을 그냥 어디 적어(memo)놨다가 다시 쓰면 어떨까?

이 기법이 바로 메모화(memoization)이다.

저 그림의 맨 왼쪽 아래부터 계산하기 시작해보자. [math]\displaystyle{ \mathrm{fib}(2) = 1 + 0 = 1 }[/math]로 채워진다. 그 위의 [math]\displaystyle{ \mathrm{fib}(3) = 1 + 1 = 2 }[/math]가 될 것이다. 이제 [math]\displaystyle{ \mathrm{fib}(4) }[/math]를 계산해야 한다. 원래는 [math]\displaystyle{ \mathrm{fib}(4) = 2 + \mathrm{fib}(2) }[/math]로 오른쪽의 [math]\displaystyle{ \mathrm{fib}(2) }[/math]를 다시 계산해야겠지만, 앞서 [math]\displaystyle{ \mathrm{fib}(2) }[/math]를 계산할 때 어디 적어뒀다면 이를 바로 읽어와 [math]\displaystyle{ \mathrm{fib}(4) = 2 + 1 = 3 }[/math]을 간단히 계산할 수 있다. 마찬가지로, [math]\displaystyle{ \mathrm{fib}(5) }[/math]의 계산 역시 [math]\displaystyle{ \mathrm{fib}(3) }[/math]의 계산 결과가 저장되어 있다면, 곧바로 [math]\displaystyle{ \mathrm{fib}(5) = 3 + 2 }[/math]라는 값을 구할 수 있다. 메모하지 않았다면 [math]\displaystyle{ \mathrm{fib}(3), \mathrm{fib}(2) }[/math] 따위를 여러번 다시 구해야 할 판인데, 계산이 확 줄어들었다.

거스름돈 문제

리브레 제국의 화폐 체계는 영 이상해서, 이 나라의 상인들은 거스름돈 계산을 힘들어 한다. 국왕인 당신은 이러한 백성들을 어엿비 녀겨 거스름돈을 계산하는 프로그램을 만들기로 결심했다.

이 나라에는 [math]\displaystyle{ x_1 }[/math]원, [math]\displaystyle{ x_2 }[/math]원, [math]\displaystyle{ \cdots , x_i }[/math]원 짜리 동전이 있고, 거슬러 주는 동전의 개수는 최대한 줄여야 한다.

행렬을 곱하는 순서

행렬을 곱할 때, 어떤 것을 먼저 곱하는지에 따라 계산량은 크게 달라진다. 계산을 가능한 한 적게 할 수 있도록, 적절히 괄호를 묶어주기 위한 알고리즘을 생각해보자.