사이클로이드

방정식[편집 | 원본 편집]

원 위의 한 점을 정하고 직선 위에서 원을 굴리면 점의 자취는 사이클로이드가 된다.

반지름의 길이가 r이고 중심이 [math]\displaystyle{ (0,r) }[/math]인 원 위의 점 [math]\displaystyle{ (0,0) }[/math]에 대해, 원을 x축 위에서 각속도 t로 굴렸을 때의 자취를 매개변수방정식으로 나타내면

[math]\displaystyle{ x=r(t-\sin t) }[/math]

[math]\displaystyle{ y=r(1-\cos t) }[/math]

이다. 이 곡선을 사이클로이드(Cycloid)라고 한다.

성질[편집 | 원본 편집]

넓이[편집 | 원본 편집]

적분을 이용해 구하기[편집 | 원본 편집]

원을 한 바퀴 굴렸을 때 사이클로이드와 x축 사이의 넓이는 다음과 같다.

[math]\displaystyle{ \begin{align} A&=\int_0^{2\pi r} ydx\\ &=\int_0^{2\pi } r(1-\cos t)\cdot r(1-\cos t)dt\\ &=\int_0^{2\pi}r^2\left(1-2\cos t+\frac{1+\cos 2 t}{2} \right)dt\\ &=r^2\left[\frac{3}{2}t-2\sin t+\frac{1}{4}\sin 2t\right]_0^{2\pi}\\ &=3\pi r^2 \end{align} }[/math]

로버벌의 증명[편집 | 원본 편집]

로버벌의 증명을 나타낸 그림.

1634년 프랑스 수학자 길리스 드 로버벌(Gilles de Roberval)은 카발리에리의 원리를 이용해 반지름이 r인 원을 굴렸을 때 만들어지는 사이클로이드의 넓이가 [math]\displaystyle{ 3\pi r^2 }[/math]임을 밝혔다. 참고로 이때는 미적분학이 발명되기 이전이었다.

반지름 r인 원을 반 바퀴 굴렸다고 하자. 사이클로이드의 각 점에서 가로축에 평행하고 가로로 평행이동했을 때 원의 내부에 포함되는 만큼의 길이를 가지는 선분을 그을 때, 끝점을 이은 곡선을 동반자 곡선(companion curve)라고 한다. 카발리에리의 원리에 의해, 사이클로이드와 동반자 곡선으로 둘러싸인 영역의 넓이는 [math]\displaystyle{ \frac{1}{2}\pi r^2 }[/math]이다. 대칭성에 의해 동반자 곡선은 직사각형을 이등분한다. 따라서 원을 한 바퀴 굴렸을 때 가로축과 사이클로이드로 둘러싸인 영역의 넓이는 [math]\displaystyle{ 2\left(\frac{1}{2}\pi r^2+\pi r^2\right)=3\pi r^2 }[/math]이다.^[1]

호의 길이[편집 | 원본 편집]

원을 한 바퀴 굴렸을 때 사이클로이드의 호의 길이(arc length)는 다음과 같다.

[math]\displaystyle{ \begin{align} l&=\int_0^{2\pi}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\\ &=\int_0^{2\pi}\sqrt{r^2(1-\cos t)^2+r^2\sin^2 t}dt\\ &=\int_0^{2\pi}\sqrt{r^2(2-2\cos t)}dt\\ &=\int_0^{2\pi}2r\sin\frac{t}{2}dt\\ &=2r\left[-2\cos\frac{t}{2}\right]_0^{2\pi}\\ &=8r \end{align} }[/math]

곡률[편집 | 원본 편집]

사이클로이드의 곡률을 [math]\displaystyle{ \kappa(t) }[/math]라고 하자. 그러면

[math]\displaystyle{ \begin{align} \kappa(t)&=\frac{|x'y''-x''y'|}{(x'^2+y'^2)^{\frac{3}{2}}}\\ &=\frac{|r(1-\cos t)r\cos t-(r\sin t) (r\sin t)|}{(r^2(1-\cos t)^2+r^2\sin^2t)^{\frac{3}{2}}}\\ &=\frac{r^2(1-\cos t)}{(r^2(2-2\cos t))^{\frac{3}{2}}}\\ &=\frac{1}{4r\left|\sin\frac{t}{2}\right|} \end{align} }[/math]

이다.

최속강하선[편집 | 원본 편집]

물체가 최단시간에 목적지에 도달하는 곡선은 사이클로이드다.

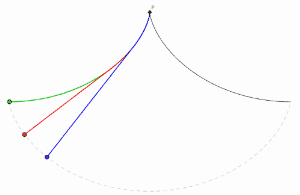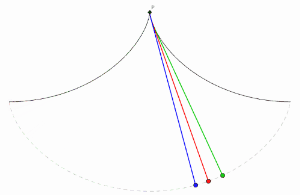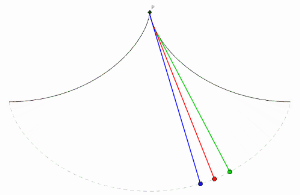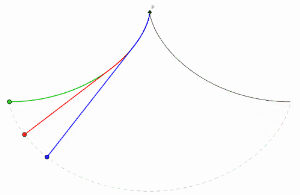
사이클로이드는 최속강하선(brachistochrone curve)이다.

[math]\displaystyle{ (0,0) }[/math]의 위치에 정지해 있는 입자가 중력을 받고 마찰없이 [math]\displaystyle{ (x_1,y_1) }[/math]로 내려간다고 가정하자. 그러면 입자가 이동한 시간 T는

[math]\displaystyle{ T=\int_{(0,0)}^{(x_1,y_1)}\frac{ds}{v} }[/math]

로 주어진다. 이때 퍼텐셜에너지가 [math]\displaystyle{ (0,0) }[/math]에서 0이라고 가정하면, 역학적 에너지는 0이고 보존되므로

[math]\displaystyle{ mgy+\frac{1}{2}mv^2=0 }[/math]

이다. 따라서

[math]\displaystyle{ v=\sqrt{-2gy} }[/math]

이다. 그러면

[math]\displaystyle{ T=\frac{1}{\sqrt{-2g}}\int_0^{y_1}\sqrt{\frac{1+(\frac{dx}{dy})^2}{y}}dy }[/math]

이다. 이제 함수 f를

[math]\displaystyle{ f\{x(y),x'(y);y\}=\sqrt{\frac{1+x'^2}{y}} }[/math]

로 정의하자. 이때

[math]\displaystyle{ \frac{\partial f}{\partial x}=0 }[/math]

이므로 오일러-라그랑주 방정식은

[math]\displaystyle{ \frac{d}{dy}\frac{\partial f}{\partial x'}=0 }[/math]

이다. 따라서

[math]\displaystyle{ \frac{\partial f}{\partial x'}=\frac{x'}{\sqrt{y(1+x'^2)}}=c }[/math]

이다. 이때 c는 상수다. 양변을 제곱해 정리하면

[math]\displaystyle{ x'^2=\frac{c^2y}{1-c^2y} }[/math]

이므로,

[math]\displaystyle{ x=\int \sqrt{\frac{c^2y}{1-c^2y}}dy }[/math]

이다. 이때

[math]\displaystyle{ y=\frac{1}{2c^2}(1-\cos\theta) }[/math]

로 치환하면

[math]\displaystyle{ x=\frac{1}{2c^2}(\theta-\sin\theta) }[/math]

가 되고, 이 곡선은 사이클로이드이다.

등시곡선[편집 | 원본 편집]

사이클로이드 위에 물체를 가만히 놓았을 때, 위치에 관계없이 최하점까지 낙하하는 시간은 같다.

사이클로이드를 이용하면 진폭에 관계없이 진동주기가 일정한 진자를 만들 수 있다.

사이클로이드는 등시곡선(tautochrone curve)이다.

변형[편집 | 원본 편집]

축소사이클로이드[편집 | 원본 편집]

축소사이클로이드(curtate cycloid)는 원 위의 점 대신 원 내부의 점을 선택했을 때 나타나는 자취이다. 원 내부의 점의 좌표를 [math]\displaystyle{ (0,r-a) }[/math]라 하면, 축소사이클로이드를 나타내는 매개변수방정식은 다음과 같다.

[math]\displaystyle{ x=rt-a\sin t }[/math]

[math]\displaystyle{ y=r-a\cos t }[/math]

[math]\displaystyle{ 0\lt |a|\lt r }[/math]

확장사이클로이드[편집 | 원본 편집]

확장사이클로이드(prolate cycloid)는 원 위의 점 대신 원 외부의 점을 선택했을 때 나타나는 자취이다. 원 내부의 점의 좌표를 [math]\displaystyle{ (0,r-a) }[/math]라 하면, 확장사이클로이드를 나타내는 매개변수방정식은 다음과 같다.

[math]\displaystyle{ x=rt-a\sin t }[/math]

[math]\displaystyle{ x=r-a\cos t }[/math]

[math]\displaystyle{ |a|\gt r }[/math]