편집 요약 없음 |
Liebesleid (토론 | 기여) 잔글 ("꼭지점"을 "꼭짓점"으로 수정) |
||
| (사용자 6명의 중간 판 8개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
'''정다면체'''(正多面體, Regular polyhedron)는 [[도형]]을 구성하는 면이 모두 [[정다각형]]이고 합동인 [[다면체]]다. '''플라톤의 입체'''(Platonic solid)라고도 한다. | |||
'''정다면체(Regular polyhedron) | 정다면체는 다음과 같은 성질을 가진다. | ||
* 각 면을 둘러싸고 있는 모서리의 개수가 같다. | * 각 면을 둘러싸고 있는 모서리의 개수가 같다. | ||
* 다면체에서 면을 하나 제거한 후 임의로 조작하면 [[평면그래프]]를 얻을 수 있다. 그러면 그 그래프의 면은 원래 다면체의 면의 수와 동일하다. | * 다면체에서 면을 하나 제거한 후 임의로 조작하면 [[평면그래프]]를 얻을 수 있다. 그러면 그 그래프의 면은 원래 다면체의 면의 수와 동일하다. | ||
| 7번째 줄: | 7번째 줄: | ||
== 종류 == | == 종류 == | ||
사실 정다면체는 다섯 가지밖에 없다. 입체가 되기 위해서는 한 | 사실 정다면체는 다섯 가지밖에 없다. 입체가 되기 위해서는 한 꼭짓점에 도형이 3개 이상 모여야 하고<ref>3차원 공간이 3개의 축으로 이루어져 있기 때문이다.</ref>그 꼭짓점에서 각도의 합이 360도 보다 작아야 하는데, 정육각형 이상부터는 이게 불가능하고, 정삼각형, 정사각형, 정오각형만이 정다면체를 만들 수 있다. 꼭짓점에서 각도의 합이 360도 미만인 경우는 정삼각형이 3개부터 5개<ref>각각 정사면체, 정팔면체, 정이십면체</ref>까지 세 가지, 정사각형과 정오각형은 각각 3개<ref>각각 정육면체, 정십이면체</ref>까지만 모일 수 있어 총 5개가 된다. | ||
{| class="wikitable" style="background:white;" width="100%" | {| class="wikitable" style="background:white;" width="100%" | ||
! 3차원 이미지 | ! 3차원 이미지 | ||
| 13번째 줄: | 13번째 줄: | ||
! 이름 | ! 이름 | ||
! 면의 모양 | ! 면의 모양 | ||
! | ! 꼭짓점의 수 | ||
! 모서리의 수 | ! 모서리의 수 | ||
! 면의 수 | ! 면의 수 | ||
! | ! 꼭짓점의 차수 | ||
|- style="text-align:center;" | |- style="text-align:center;" | ||
| [[파일:tetrahedron.svg]] | | [[파일:tetrahedron.svg|100px]] | ||
| [[파일:Schlegeldiagramm des Tetraeders.svg]] | | [[파일:Schlegeldiagramm des Tetraeders.svg|100px]] | ||
|정사면체 | |정사면체 | ||
| 삼각형 | | 삼각형 | ||
| 27번째 줄: | 27번째 줄: | ||
| 3 | | 3 | ||
|- style="text-align:center;" | |- style="text-align:center;" | ||
| [[파일:hexahedron.svg]] | | [[파일:hexahedron.svg|100px]] | ||
| [[파일:Cube graph.png]] | | [[파일:Cube graph.png|100px]] | ||
|정육면체 | |정육면체 | ||
| 사각형 | | 사각형 | ||
| 36번째 줄: | 36번째 줄: | ||
| 3 | | 3 | ||
|- style="text-align:center;" | |- style="text-align:center;" | ||
| [[파일:octahedron.svg]] | | [[파일:octahedron.svg|100px]] | ||
| [[파일:Octahedron graph.png]] | | [[파일:Octahedron graph.png|100px]] | ||
|정팔면체 | |정팔면체 | ||
| 삼각형 | | 삼각형 | ||
| 45번째 줄: | 45번째 줄: | ||
| 4 | | 4 | ||
|- style="text-align:center;" | |- style="text-align:center;" | ||
| [[파일:dodecahedron.svg]] | | [[파일:dodecahedron.svg|100px]] | ||
| [[파일:Graph of 20-fullerene w-nodes.svg]] | | [[파일:Graph of 20-fullerene w-nodes.svg|100px]] | ||
|정십이면체 | |정십이면체 | ||
| 오각형 | | 오각형 | ||
| 54번째 줄: | 54번째 줄: | ||
| 3 | | 3 | ||
|- style="text-align:center;" | |- style="text-align:center;" | ||
| [[파일:icosahedron.svg]] | | [[파일:icosahedron.svg|100px]] | ||
| [[파일:Icosahedron graph.svg]] | | [[파일:Icosahedron graph.svg|100px]] | ||
|정이십면체 | |정이십면체 | ||
| 삼각형 | | 삼각형 | ||
| 63번째 줄: | 63번째 줄: | ||
| 5 | | 5 | ||
|} | |} | ||
정다면체는 평면그래프이므로, 정다면체의 | 정다면체는 평면그래프이므로, 정다면체의 꼭짓점의 개수, 모서리의 개수, 면의 개수를 각각 <math>v,e,f</math>라 하면 <math>v-e+f=2</math>이다([[오일러의 정리]]). 한편 그래프의 꼭짓점의 차수를 ''d''라고 하면 모든 꼭짓점의 차수의 합이 모서리의 수의 두 배이므로 <math>vd=2e</math>이고 정다면체를 이루는 정다각형이 ''n''다각형이면 <math>nf=2e</math>이다. 식을 잘 조작하면 | ||
: <math>\frac{1}{d}+\frac{1}{n}=\frac{1}{e}+\frac{1}{2}</math> | : <math>\frac{1}{d}+\frac{1}{n}=\frac{1}{e}+\frac{1}{2}</math> | ||
을 얻는다. 한편 <math>n\ge 3, d\ge 3</math>이면서 동시에 <math>\frac{1}{d}+\frac{1}{n}> \frac{1}{2}</math>이어야 하므로 ''d''와 ''n'' 둘 모두 6보다 작다. | 을 얻는다. 한편 <math>n\ge 3, d\ge 3</math>이면서 동시에 <math>\frac{1}{d}+\frac{1}{n}> \frac{1}{2}</math>이어야 하므로 ''d''와 ''n'' 둘 모두 6보다 작다. | ||
| 70번째 줄: | 70번째 줄: | ||
* <math>n=5</math>일 때, <math>\frac{1}{d}-\frac{1}{e}=\frac{3}{10}</math>을 만족하는 (''d'',''e'')는 <math>(3,30)</math>이다. | * <math>n=5</math>일 때, <math>\frac{1}{d}-\frac{1}{e}=\frac{3}{10}</math>을 만족하는 (''d'',''e'')는 <math>(3,30)</math>이다. | ||
각 해에서 면의 수를 구하면 4, 8, 20, 6, 12이다. | 각 해에서 면의 수를 구하면 4, 8, 20, 6, 12이다. | ||
== | |||
== 정다면체의 확장 == | |||
[[분류: | 정다면체에서 만나는 다각형 조건을 별정다각형을 포함하고, 꼭짓점에서 별모양처럼 만나는 경우를 포함시키면 4개의 정다면체를 더 얻을 수 있다. 이 것을 [[케플러-푸앵소 다면체]]라고 부른다. | ||
== 같이 보기 == | |||
* [[정다포체]]: 4차원의 정다면체 | |||
{{주석}} | |||
[[분류:정다면체|*]] | |||
[[분류:그래프 이론]] | [[분류:그래프 이론]] | ||
2020년 9월 7일 (월) 22:42 기준 최신판
정다면체(正多面體, Regular polyhedron)는 도형을 구성하는 면이 모두 정다각형이고 합동인 다면체다. 플라톤의 입체(Platonic solid)라고도 한다.
정다면체는 다음과 같은 성질을 가진다.
- 각 면을 둘러싸고 있는 모서리의 개수가 같다.
- 다면체에서 면을 하나 제거한 후 임의로 조작하면 평면그래프를 얻을 수 있다. 그러면 그 그래프의 면은 원래 다면체의 면의 수와 동일하다.
- 꼭짓점과 연결된 변의 개수는 동일하다. 그래프로 간주하면, 각 꼭짓점의 차수는 모두 같다.
종류[편집 | 원본 편집]
사실 정다면체는 다섯 가지밖에 없다. 입체가 되기 위해서는 한 꼭짓점에 도형이 3개 이상 모여야 하고[1]그 꼭짓점에서 각도의 합이 360도 보다 작아야 하는데, 정육각형 이상부터는 이게 불가능하고, 정삼각형, 정사각형, 정오각형만이 정다면체를 만들 수 있다. 꼭짓점에서 각도의 합이 360도 미만인 경우는 정삼각형이 3개부터 5개[2]까지 세 가지, 정사각형과 정오각형은 각각 3개[3]까지만 모일 수 있어 총 5개가 된다.
| 3차원 이미지 | 그래프 이미지 | 이름 | 면의 모양 | 꼭짓점의 수 | 모서리의 수 | 면의 수 | 꼭짓점의 차수 |
|---|---|---|---|---|---|---|---|

|
|
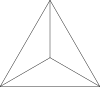
정사면체 | 삼각형 | 4 | 6 | 4 | 3 |

|

|
정육면체 | 사각형 | 8 | 12 | 6 | 3 |

|

|
정팔면체 | 삼각형 | 6 | 12 | 8 | 4 |

|

|
정십이면체 | 오각형 | 20 | 30 | 12 | 3 |

|
|
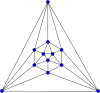
정이십면체 | 삼각형 | 12 | 30 | 20 | 5 |
정다면체는 평면그래프이므로, 정다면체의 꼭짓점의 개수, 모서리의 개수, 면의 개수를 각각 [math]\displaystyle{ v,e,f }[/math]라 하면 [math]\displaystyle{ v-e+f=2 }[/math]이다(오일러의 정리). 한편 그래프의 꼭짓점의 차수를 d라고 하면 모든 꼭짓점의 차수의 합이 모서리의 수의 두 배이므로 [math]\displaystyle{ vd=2e }[/math]이고 정다면체를 이루는 정다각형이 n다각형이면 [math]\displaystyle{ nf=2e }[/math]이다. 식을 잘 조작하면
- [math]\displaystyle{ \frac{1}{d}+\frac{1}{n}=\frac{1}{e}+\frac{1}{2} }[/math]
을 얻는다. 한편 [math]\displaystyle{ n\ge 3, d\ge 3 }[/math]이면서 동시에 [math]\displaystyle{ \frac{1}{d}+\frac{1}{n}\gt \frac{1}{2} }[/math]이어야 하므로 d와 n 둘 모두 6보다 작다.
- [math]\displaystyle{ n=3 }[/math]일 때, [math]\displaystyle{ \frac{1}{d}-\frac{1}{e}=\frac{1}{6} }[/math]을 만족하는 (d,e)는 [math]\displaystyle{ (3,6),(4,12),(5,30) }[/math]이다.
- [math]\displaystyle{ n=4 }[/math]일 때, [math]\displaystyle{ \frac{1}{d}-\frac{1}{e}=\frac{1}{4} }[/math]을 만족하는 (d,e)는 [math]\displaystyle{ (3,12) }[/math]이다.
- [math]\displaystyle{ n=5 }[/math]일 때, [math]\displaystyle{ \frac{1}{d}-\frac{1}{e}=\frac{3}{10} }[/math]을 만족하는 (d,e)는 [math]\displaystyle{ (3,30) }[/math]이다.
각 해에서 면의 수를 구하면 4, 8, 20, 6, 12이다.
정다면체의 확장[편집 | 원본 편집]
정다면체에서 만나는 다각형 조건을 별정다각형을 포함하고, 꼭짓점에서 별모양처럼 만나는 경우를 포함시키면 4개의 정다면체를 더 얻을 수 있다. 이 것을 케플러-푸앵소 다면체라고 부른다.
같이 보기[편집 | 원본 편집]
- 정다포체: 4차원의 정다면체