3대 작도 불가능 문제는 고대 그리스 때부터 제기된 작도 문제이며, 무려 2000년 이상이 걸려서 풀렸다! 세 질문은 다음과 같다:
- 주어진 정육면체의 두 배의 부피를 갖는 정육면체의 한 변을 작도할 수 있는가? 즉, [math]\displaystyle{ \sqrt[3] 2 }[/math]가 작도 가능한 수인가?
- 주어진 원과 같은 넓이를 갖는 정사각형을 작도할 수 있는가? 즉 [math]\displaystyle{ \sqrt \pi }[/math]가 작도 가능한 수인가?
- 임의의 각을 삼등분할 수 있는가? 즉 임의의 각 [math]\displaystyle{ \alpha }[/math]에 대해, [math]\displaystyle{ \cos \alpha }[/math] (또는 [math]\displaystyle{ \sin \alpha }[/math])가 작도 가능한 수인가?
답은 모두 NO이다. 증명은 field theory 하나만 있으면 발로도 풀 수 있을 정도로 쉽다. 물론 그 전 과정을 생각해 내는 게 매우 어렵기는 하지만. 이것이 field theory라는 'tool'의 힘이라고 할 수 있다.
이 문제는 유사수학자들이 매우 좋아한다. 이들은 0.999...=1과 더불어 이 세 문제를 수학계의 영원한 떡밥으로 여겨 자신이 위의 셋 중 하나를 '가능하다'고 증명했다고 주장한다. 물론, 당연히 틀렸다. 이런 사람들은 상대해 주지 않고 가는 게 최선의 방법이다.
1 작도 가능한 수[편집]
실수 [math]\displaystyle{ \alpha }[/math]에 대하여, [math]\displaystyle{ |\alpha| }[/math]를 길이로 가지는 선분을 작도할 수 있으면 [math]\displaystyle{ \alpha }[/math]를 작도 가능한 수(constructible number)라고 한다.
그러면 작도 가능한 수의 집합은 무엇일까? 어떤 수만이 작도 가능할까? 일단 다음 두 성질을 알 수 있다.
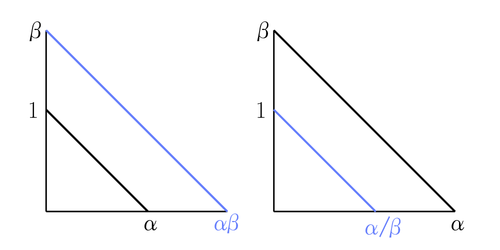
- 모든 유리수는 작도할 수 있다. 더 나아가, 작도 가능한 수들의 사칙연산은 모두 작도 가능하다.
- Proof. 덧셈과 뺄셈은 너무 간단하고, 곱셈과 나눗셈은 다음 그림에서 쉽게 증명된다.
- 따라서 작도 가능한 수의 모임은 [math]\displaystyle{ \mathbb Q }[/math]를 포함하는 [math]\displaystyle{ \mathbb R }[/math]의 subfield가 된다.
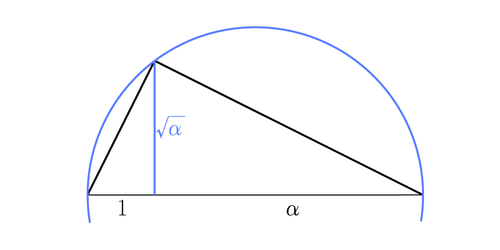
- 작도 가능한 수의 제곱근도 작도 가능하다.
그런데, 처음 우리가 작도 가능함을 알고 있는 수는 단 하나, 1뿐이다. 1만이 주어지며, 다른 것들은 1에서 작도한다. 1에서 출발하여, 모든 유리수를 작도할 수 있고, 또한 어떤 유리수의 제곱근을 작도할 수 있고, 유리수와 그 제곱근의 합과 곱을 작도할 수 있고, ... 이 과정을 반복한다. 즉, 우리가 작도할 수 있는 수 [math]\displaystyle{ \alpha }[/math]는 다음과 같이 구성된다.
- 우리가 알고 있는 [math]\displaystyle{ \mathbb Q }[/math]
- [math]\displaystyle{ \lt }[/math] 어떤 무리수 [math]\displaystyle{ \sqrt{q_1}\notin \mathbb Q }[/math] ([math]\displaystyle{ q_1 \in \mathbb Q }[/math])를 추가하여 만든 field extension [math]\displaystyle{ \mathbb Q(\sqrt{q_1}) }[/math]
- [math]\displaystyle{ \lt \cdots }[/math]
- [math]\displaystyle{ \lt }[/math]어떤 무리수 [math]\displaystyle{ \sqrt{q_i}\notin \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i-1}}) }[/math] ([math]\displaystyle{ q_i \in \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i-1}}) }[/math])를 추가하여 만든 field extension [math]\displaystyle{ \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i-1}}, \sqrt{q_i}) }[/math]
- [math]\displaystyle{ \ni \alpha }[/math]
여기에서 알 수 있는 것은, 각 단계의 차원, 즉 다음 단계의 field를 전 단계의 field의 vector space로 간주하고 구한 차원이
- [math]\displaystyle{ \operatorname{dim}_{ \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i-1}})} \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i}}) = [ \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i}}): \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{i-1}})] = 2 }[/math]
이므로, [math]\displaystyle{ [ \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{n}}):\mathbb Q ] = 2^n }[/math]인 것도 알 수 있다. 또한 [math]\displaystyle{ \mathbb Q (\alpha) \le \mathbb Q(\sqrt{q_1}, \cdots , \sqrt{q_{n}}) }[/math]이므로, [math]\displaystyle{ [\mathbb Q(\alpha):\mathbb Q] }[/math]는 2의 거듭제곱이어야 한다!
2 그런데 말입니다[편집]
위에서, [math]\displaystyle{ \alpha }[/math]가 작도 가능하려면 [math]\displaystyle{ \exists m \in \mathbb N_0: \; [\mathbb Q(\alpha):\mathbb Q] = 2^m }[/math]이어야 함을 보였다. 그런데,
- [math]\displaystyle{ [\mathbb Q (\sqrt[3] 2):\mathbb Q] = 3 }[/math]이다. 작도 불가능하다.
- [math]\displaystyle{ \pi }[/math]는 대수적 수조차 아니므로, [math]\displaystyle{ \sqrt \pi }[/math]도 작도 불가능하다.
- [math]\displaystyle{ \cos 20^\circ }[/math]를 생각해 보자. Cosine의 3배각 공식을 사용하면,
- [math]\displaystyle{ 8 \cos^3 20^\circ - 6 \cos 20^\circ - 1 = 0 }[/math]
- 인데, 이것은 [math]\displaystyle{ \mathbb Q }[/math]에서 기약 다항식이므로, [math]\displaystyle{ [\mathbb Q ( \cos^3 20^\circ ):\mathbb Q] = 3 }[/math]이다! 저 다항식이 기약이라는 것은, 대입 심층면접에도 나온 전과가 있다. (...) 계수비교를 하거나 유리근 정리를 쓰면 쉽게(?) 해결된다.
결국, 위의 세 수는 모두 작도 불가능한 수이다.
3 작도 가능성의 필요충분조건[편집]
[math]\displaystyle{ \alpha }[/math]가 작도 가능하다면 [math]\displaystyle{ [\mathbb Q(\alpha):\mathbb Q] }[/math]는 2의 거듭제곱이어야 한다는 것을 위에서 증명했다. 그러면, 이 역도 성립할까? 그 답은 NO이지만, 이를 Galois theory의 도움을 받아 필요충분조건을 찾을 수 있다!
- [math]\displaystyle{ \alpha \in \mathbb R }[/math]일 때, [math]\displaystyle{ K }[/math]가 [math]\displaystyle{ \mathbb Q(\alpha) / \mathbb Q }[/math]의 normal closure이면, [math]\displaystyle{ \alpha }[/math]가 작도 가능할 필요충분조건이 [math]\displaystyle{ \exists m \in \mathbb N_0: \; [K:\mathbb Q] = 2^m }[/math]인 것이다.
4 참고문헌[편집]
- 이인석, 대수학, 서울대학교출판부, pp. 206-209.