폴라드 로 소인수분해법(Pollard's rho factorization algorithm)은 큰 수를 소인수분해하는 알고리즘으로, 1975년 존 폴라드(John Pollard)가 고안하였다. 이 알고리즘은 타 소인수분해법보다 계산 과정이 비교적 간단하고 직접 나누기보다 빠르다.
아이디어[편집 | 원본 편집]
소인수분해하려는 합성수 [math]\displaystyle{ N=pq }[/math]가 주어져 있고 우리가 구하려는 값은 소인수 [math]\displaystyle{ p }[/math]이다.
함수 [math]\displaystyle{ g(x)=x^2+1 \mod N }[/math]을 정의하고 이 함수로 수열을 정의한다. [math]\displaystyle{ \{x_n\}: x_{n+1}=g(x_n) }[/math] 함수를 이렇게 정의하는 이유는 이차식 자체의 특징보다는 유사 난수를 생성하는 데 목적이 있다.
기본적으로 [math]\displaystyle{ x_n \in \{0, 1, 2, \cdots N-1 \}, x_n \mod p \in \{0, 1, 2, \cdots p-1 \} }[/math]가 성립한다. 그리고 우리가 포착해낼 부분은 [math]\displaystyle{ x_i \equiv x_j \pmod p }[/math]를 만족하는 두 항을 찾는 것이다.
만약 [math]\displaystyle{ x_i \equiv x_{i+k} \pmod p }[/math]이면 모든 [math]\displaystyle{ m \geq 1 }[/math]에 대해 [math]\displaystyle{ x_{i+m} \equiv x_{i+k+m} \pmod p }[/math]도 성립한다. 다시 말해 수열의 항은 [math]\displaystyle{ x_i }[/math] 이후 [math]\displaystyle{ k }[/math] 또는 그의 약수를 주기로 순환한다는 사실을 알 수 있다. 단, [math]\displaystyle{ m\lt 0 }[/math]인 경우는 성립 여부를 알 수 없다.
첫 항을 아무거나 지정하고 [math]\displaystyle{ x_0, x_1, x_2, \cdots }[/math]를 차례대로 셈해 나간다고 할 때, 처음 몇 항끼리는 같은 수를 찾지 못할 것이다. 하지만 점차 [math]\displaystyle{ x_n \mod p }[/math] 내에서 수를 계속해서 골라 나간다면, 어느 순간 에서 [math]\displaystyle{ p }[/math]로 나눈 나머지가 일치하는 두 점이 나올 것이다. 이때 각 수열의 항은 사실상 난수를 하나씩 고르는 것과 비슷한데, "일치하는 쌍"이 하나 이상 나오기 위한 난수의 개수는 [math]\displaystyle{ p }[/math]보다는 훨씬 적다. 좀 더 구체적으로는 대략 [math]\displaystyle{ O(\sqrt{p}) }[/math]개 골라야 한다.
생일 문제에 비유하면 이렇다: 사람들을 무작위로 골라서 생일을 물어볼 때, 생일이 같은 두 사람이 존재할 확률은 23명일 때 50%, 50명일 때 97%, 60명 이상이면 99%를 넘는다. 즉 366명보다 훨씬 적은 수를 골라도 "일치하는 쌍"을 쉽게 찾을 수가 있으며, 이것이 본 문서의 기본 아이디어이다.
소인수를 발견하는 방법[편집 | 원본 편집]
그렇다면 일정 개수만큼 골라서 [math]\displaystyle{ x_0, x_1, x_2, \cdots x_{r-1} }[/math]를 메모리에 저장하고, 두 개 고르고 [math]\displaystyle{ \gcd(x_i-x_j, N)=p }[/math]인 순서쌍을 찾으면 될 것이다. 하지만 이 방식에는 꽤 큰 결점이 있는데, [math]\displaystyle{ r }[/math]개 항 중 두 개를 골라서 비교하는 횟수는 총 [math]\displaystyle{ \begin{pmatrix} r \\ 2 \end{pmatrix} }[/math]회, 즉 대략 항 개수의 제곱에 비례한다고 할 수 있다. 더구나 찾고 싶은 값인 [math]\displaystyle{ p }[/math]가 얼마나 큰 값인지 가늠할 방법이 없는 와중에 무턱대고 계산한 항을 일일이 메모리에 기록해 두는 것은 매우 비효율적이다.
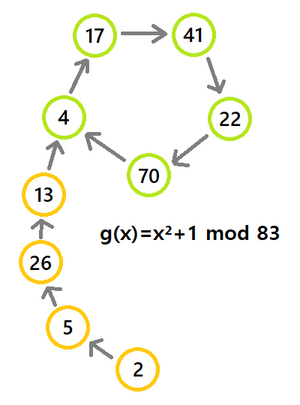
이 부분을 개선하려면 접근 방식을 달리 해야 한다. 먼저 주어진 수열에 대해 [math]\displaystyle{ x_i }[/math]를 [math]\displaystyle{ x_i \equiv x_j \pmod p, i\lt j }[/math]가 성립하는 두 항이 존재하는 최초의 항이라 하자. 즉 [math]\displaystyle{ x_0, x_1, \cdots x_{i-1} }[/math]까지는 순환하지 않고, 그 다음에는 [math]\displaystyle{ x_i, \cdots x_{j-1} }[/math] 묶음으로 순환하는 구도이다. 물론 [math]\displaystyle{ i=0 }[/math]과 같이 처음부터 순환하는 경우도 나올 수 있다.[1] 이를 다이어그램으로 그려보면 로(ρ)자 모양의 유향 그래프가 만들어진다. (오른쪽 그림 참고) 이 알고리즘에 '로'가 붙은 것도 이 때문이다.
그 다음 다이어그램 상에서 첫 항에 토끼와 거북이가 서 있다. 이제 거북이는 한 번에 한 칸을, 토끼는 두 칸을 달릴 것이다. 이렇게 설정하면 토끼와 거북이는 순환 시작점이나 순환 고리의 길이에 관계 없이 어느 순간에서 반드시 만난다.
이에 착안하여 두 수열을 정의할 것이다. 하나는 앞서 언급한 [math]\displaystyle{ \{x_n \} }[/math]으로, 바로 위 문단에서 거북이 역할을 한다. 그 다음 원래 수열에서 항을 두 칸씩 뛰는 수열, 즉 [math]\displaystyle{ \{y_n\}: y_0=x_0, y_{n+1}=g(g(y_n))=x_{2n+2} }[/math]를 정의하고, 이는 토끼 역할을 한다. 또한 수열의 각 항의 값은 메모리에 누적해서 추가할 필요는 없고 최신 항만 저장하면 된다.
알고리즘[편집 | 원본 편집]
합성수 [math]\displaystyle{ N }[/math]과 계산 반복 횟수[math]\displaystyle{ M }[/math]을 입력 받고 아래 과정을 시행한다.
- 초깃값 [math]\displaystyle{ x_0=y_0=a, d_0=1 }[/math]를 설정한다. [math]\displaystyle{ a }[/math]는 아무 값이나 상관 없고 보통 2를 고른다.
- [math]\displaystyle{ x_{n+1}=x_n^2+1, y_{n+1}=(y_n^2+1)^2+1, d_{n+1}=d_n(x_{n+1}-y_{n+1})\ (n \geq 0) }[/math]을 셈한다. 모든 연산은 [math]\displaystyle{ \mathbb{Z}/N\mathbb{Z} }[/math] 내에서, 즉 [math]\displaystyle{ N }[/math]으로 나눈 나머지로 셈한다.
- 위 계산을 반복하여 [math]\displaystyle{ d_M }[/math]을 도출하고 [math]\displaystyle{ g=\gcd(d_M, N) }[/math]을 셈한다.
- [math]\displaystyle{ 1\lt g\lt N }[/math]이면 [math]\displaystyle{ N=g \cdot (N/g) }[/math]를 출력한다. (알고리즘 성공)
- [math]\displaystyle{ g=1 }[/math]이면 [math]\displaystyle{ M }[/math]의 값을 올려서 계산을 이어나가거나 '실패'를 출력한다.
- [math]\displaystyle{ g=N }[/math]이면 [math]\displaystyle{ M }[/math]의 값을 내리고 되돌아가거나 '실패'를 출력한다.
적용 예[편집 | 원본 편집]
[math]\displaystyle{ N=328583 }[/math]을 폴라드 로 소인수분해법으로 나눠보자. [math]\displaystyle{ x_0=y_0=2, d_0=1, M=30 }[/math]으로 놓고 위 방법대로 계산을 반복하면 아래 표와 같이 전개된다.
| [math]\displaystyle{ n }[/math] | [math]\displaystyle{ x_n }[/math] | [math]\displaystyle{ y_n }[/math] | [math]\displaystyle{ x_n-y_n }[/math] | [math]\displaystyle{ d_n }[/math] |
|---|---|---|---|---|
| 1 | 5 | 26 | -21 | 328562 |
| 2 | 26 | 129747 | -129721 | 95477 |
| 3 | 677 | 77071 | -76394 | 15496 |
| 4 | 129747 | 250465 | -120718 | 305474 |
| 5 | 319754 | 157823 | 161931 | 168308 |
| 6 | 77071 | 37127 | 39944 | 86572 |
| 7 | 144151 | 15515 | 128636 | 269339 |
| 8 | 250465 | 253481 | -3016 | 259335 |
| 9 | 307032 | 164902 | 142130 | 156942 |
| 10 | 157823 | 304419 | -146596 | 312228 |
| 11 | 193598 | 48302 | 145296 | 324759 |
| 12 | 37127 | 34034 | 3093 | 1356 |
| 13 | 8445 | 285647 | -277202 | 13040 |
| 14 | 15515 | 25920 | -10405 | 23579 |
| 15 | 192470 | 98253 | 94217 | 321563 |
| 16 | 253481 | 219843 | 33638 | 112417 |
| 17 | 183210 | 56170 | 127040 | 252751 |
| 18 | 164902 | 274952 | -110050 | 289149 |
| 19 | 126274 | 236755 | -110481 | 25757 |
| 20 | 304419 | 321429 | -17010 | 203152 |
| 21 | 6906 | 301730 | -294824 | 23992 |
| 22 | 48302 | 233504 | -185202 | 61525 |
| 23 | 143905 | 235201 | -91296 | 139985 |
| 24 | 34034 | 183639 | -149605 | 110163 |
| 25 | 58082 | 41187 | 16895 | 109773 |
| 26 | 285647 | 290512 | -4865 | 230313 |
| 27 | 149467 | 171591 | -22124 | 220352 |
| 28 | 25920 | 106960 | -81040 | 174221 |
| 29 | 222749 | 201408 | 21341 | 133716 |
| 30 | 98253 | 190110 | -91857 | 10511 |
이제 계산 최종 결과인 [math]\displaystyle{ d_{30}=10511 }[/math]을 불러와서 최대공약수를 셈한다. [math]\displaystyle{ \gcd(d_{30}, N)=457 }[/math]로 비자명한 약수를 찾았고, [math]\displaystyle{ N=457 \cdot 719 }[/math]임을 알아내어 알고리즘은 성공이다.
이 알고리즘이 통하는 이유는 서로 다른 소인수 457, 719에 대해 [math]\displaystyle{ x_n, y_n }[/math]의 순환 사이클이 다르기 때문이다. 실제로 [math]\displaystyle{ x_n-y_n }[/math]을 457, 719로 나눈 나머지를 각각 셈해보면 [math]\displaystyle{ x_n-y_n \equiv 0 \pmod{457} }[/math]을 만족하는 [math]\displaystyle{ n }[/math]의 최솟값은 30이지만 [math]\displaystyle{ x_n-y_n \equiv 0 \pmod{719} }[/math]의 경우 36이다. 즉 위에서 설정한 항의 개수는 [math]\displaystyle{ 30 \leq M \lt 36 }[/math]이었기에, [math]\displaystyle{ 457 \mid d_M \text{ and } 719 \nmid d_M }[/math]가 성립하고, 그에 따라 [math]\displaystyle{ 1 \lt \gcd(d_M, N) \lt N }[/math] 조건이 들어맞아서 소인수를 찾을 수 있었던 것이다. 만약 [math]\displaystyle{ M\lt 30 }[/math]이었다면 최대공약수 값은 1이고, [math]\displaystyle{ M \geq 36 }[/math]이었다면 [math]\displaystyle{ d_M \equiv 0 \pmod N }[/math]이 되어버려 최대공약수가 원래 수와 일치하였을 것이다.
그런데 다른 소인수에 대해 [math]\displaystyle{ x_n-y_n \equiv 0 \pmod{p, q} }[/math]를 만족하는 가장 빠른 항이 서로 일치하는 경우가 가끔 있다. 소인수의 크기가 비슷할 때 일어나기 쉬우며, 비자명한 약수를 찾을 수 없다. 이 경우 초깃값을 2 대신 다른 값을 넣거나, [math]\displaystyle{ g(x) }[/math]의 식을 바꿔서 다시 시도할 수 있다.
각주
- ↑ 술 게임 중 '더 게임 오브 데스'를 떠올리면 이해가 쉬울 것이다. 한 사람이 무작위로 다음 사람을 가리킬 때, 처음 몇 명에서는 한 번만 지나치다가 어느 시점부터는 몇 사람 내에서 순환한다.
수론 알고리즘 |
|
|---|---|
| 정수의 곱셈 | |
| 소수판정법 | |
| 소인수분해 | |
| 기타 알고리즘 | |