개요[편집 | 원본 편집]
삼각형과 사다리꼴에서만 성립하는 기하학의 정리 중 하나. 한국의 수학 교육과정에선 중학교 때 배우게 되며, 삼각형의 중점연결정리만을 배우고, 사다리꼴에서는 "알아서 해"라는 식으로 넘긴다.
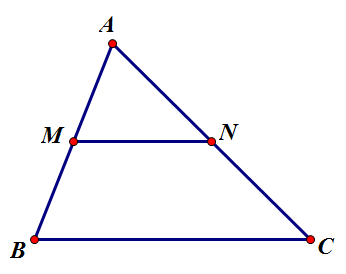
삼각형의 중점연결정리[편집 | 원본 편집]
“ 삼각형 [math]\displaystyle{ \triangle{ABC} }[/math]에서, [math]\displaystyle{ \overline{AB} }[/math]의 중점 [math]\displaystyle{ M }[/math], [math]\displaystyle{ \overline{AC} }[/math]의 중점 [math]\displaystyle{ N }[/math]을 이은 선분은 [math]\displaystyle{ \overline{BC} }[/math]에 평행하며, 더욱이 [math]\displaystyle{ \overline{BC} }[/math]의 길이의 절반이다. 역으로, [math]\displaystyle{ \overline{AB} }[/math]의 중점 [math]\displaystyle{ M }[/math]에서 [math]\displaystyle{ \overline{BC}/ }[/math]에 평행한 직선을 그었을 때, [math]\displaystyle{ \overline{AC} }[/math]와 만나는 점을 [math]\displaystyle{ N }[/math]이라 하면 [math]\displaystyle{ N }[/math]은 [math]\displaystyle{ \overline{AC} }[/math]의 중점이다. “
증명[편집 | 원본 편집]
[math]\displaystyle{ \overline{AB}:\overline{AM}=2:1,\,\overline{AC}:\overline{AN}=2:1,\,\angle{A} }[/math]는 공통이므로 [math]\displaystyle{ \triangle{AMN}\sim\triangle{ABC} }[/math](SAS 닮음)이다. 따라서 [math]\displaystyle{ \overline{BC}:\overline{MN}=2:1 }[/math]이고, [math]\displaystyle{ \angle{AMN}=\angle{ABC} }[/math]이므로 [math]\displaystyle{ \overline{MN}\parallel\overline{BC} }[/math](동위각)이다.
역의 증명은 다음과 같다.
[math]\displaystyle{ \angle{AMN}=\angle{ABC} }[/math]이고, [math]\displaystyle{ \angle{A} }[/math]는 공통이므로 [math]\displaystyle{ \triangle{AMN}\sim\triangle{ABC} }[/math](AA 닮음)이다. 또한, 닮음비는 [math]\displaystyle{ \overline{AM}:\overline{AB}=1:2 }[/math]이므로, [math]\displaystyle{ \overline{AN}:\overline{AC}=1:2 }[/math]이다.
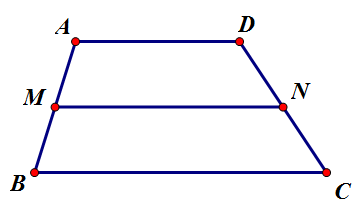
사다리꼴의 중점연결정리[편집 | 원본 편집]
“ 사다리꼴 [math]\displaystyle{ ABCD }[/math]에서, [math]\displaystyle{ \overline{AB} }[/math]의 중점 [math]\displaystyle{ M }[/math], [math]\displaystyle{ \overline{CD} }[/math]의 중점 [math]\displaystyle{ N }[/math]을 이은 선분은 [math]\displaystyle{ \overline{AD},\overline{BC} }[/math]에 평행하고, [math]\displaystyle{ \overline{MN}=\frac{\overline{AD}+\overline{BC}}{2} }[/math]이다. “
증명[편집 | 원본 편집]
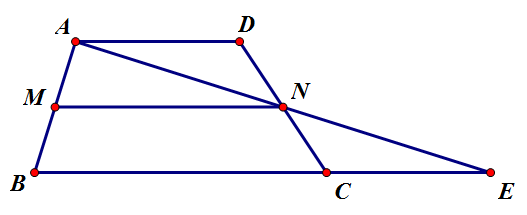[math]\displaystyle{ \overline{AN} }[/math]의 연장선과 [math]\displaystyle{ \overline{BC} }[/math]의 연장선이 만나는 점을 [math]\displaystyle{ E }[/math]라 하자. 그럼 [math]\displaystyle{ \overline{DN}=\overline{NC},\,\angle{AND}=\angle{ENC} }[/math](맞꼭지각), [math]\displaystyle{ \angle{ADN}=\angle{ECN} }[/math](엇각)이므로 [math]\displaystyle{ \triangle{AND}\cong\triangle{ENC} }[/math](ASA 합동)이다. 따라서 [math]\displaystyle{ \overline{AD}=\overline{EC} }[/math]이고, 삼각형 [math]\displaystyle{ \triangle{ABE} }[/math]에서 중점연결정리에 의해 [math]\displaystyle{ \overline{MN}\parallel\overline{BC}\parallel\overline{AD} }[/math], 그리고 [math]\displaystyle{ \overline{MN}=\frac{\overline{BC}+\overline{CE}}{2}=\frac{\overline{BC}+\overline{AD}}{2} }[/math]가 성립한다.