정다면체

정다면체(正多面體, Regular polyhedron)는 도형을 구성하는 면이 모두 정다각형이고 합동인 다면체다. 플라톤의 입체(Platonic solid)라고도 한다.

정다면체는 다음과 같은 성질을 가진다.

• 각 면을 둘러싸고 있는 모서리의 개수가 같다.
• 다면체에서 면을 하나 제거한 후 임의로 조작하면 평면그래프를 얻을 수 있다. 그러면 그 그래프의 면은 원래 다면체의 면의 수와 동일하다.
• 꼭짓점과 연결된 변의 개수는 동일하다. 그래프로 간주하면, 각 꼭짓점의 차수는 모두 같다.

종류

사실 정다면체는 다섯 가지밖에 없다. 입체가 되기 위해서는 한 꼭짓점에 도형이 3개 이상 모여야 하고그 꼭짓점에서 각도의 합이 360도 보다 작아야 하는데, 정육각형 이상부터는 이게 불가능하고, 정삼각형, 정사각형, 정오각형만이 정다면체를 만들 수 있다. 꼭짓점에서 각도의 합이 360도 미만인 경우는 정삼각형이 3개부터 5개까지 세 가지, 정사각형과 정오각형은 각각 3개까지만 모일 수 있어 총 5개가 된다.

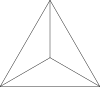
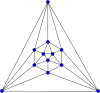
3차원 이미지	그래프 이미지	이름	면의 모양	꼭짓점의 수	모서리의 수	면의 수	꼭짓점의 차수
		정사면체	삼각형	4	6	4	3
		정육면체	사각형	8	12	6	3
		정팔면체	삼각형	6	12	8	4
		정십이면체	오각형	20	30	12	3
		정이십면체	삼각형	12	30	20	5

정다면체는 평면그래프이므로, 정다면체의 꼭짓점의 개수, 모서리의 개수, 면의 개수를 각각 [math]\displaystyle{ v,e,f }[/math]라 하면 [math]\displaystyle{ v-e+f=2 }[/math]이다(오일러의 정리). 한편 그래프의 꼭짓점의 차수를 d라고 하면 모든 꼭짓점의 차수의 합이 모서리의 수의 두 배이므로 [math]\displaystyle{ vd=2e }[/math]이고 정다면체를 이루는 정다각형이 n다각형이면 [math]\displaystyle{ nf=2e }[/math]이다. 식을 잘 조작하면

[math]\displaystyle{ \frac{1}{d}+\frac{1}{n}=\frac{1}{e}+\frac{1}{2} }[/math]

을 얻는다. 한편 [math]\displaystyle{ n\ge 3, d\ge 3 }[/math]이면서 동시에 [math]\displaystyle{ \frac{1}{d}+\frac{1}{n}\gt \frac{1}{2} }[/math]이어야 하므로 d와 n 둘 모두 6보다 작다.

• [math]\displaystyle{ n=3 }[/math]일 때, [math]\displaystyle{ \frac{1}{d}-\frac{1}{e}=\frac{1}{6} }[/math]을 만족하는 (d,e)는 [math]\displaystyle{ (3,6),(4,12),(5,30) }[/math]이다.
• [math]\displaystyle{ n=4 }[/math]일 때, [math]\displaystyle{ \frac{1}{d}-\frac{1}{e}=\frac{1}{4} }[/math]을 만족하는 (d,e)는 [math]\displaystyle{ (3,12) }[/math]이다.
• [math]\displaystyle{ n=5 }[/math]일 때, [math]\displaystyle{ \frac{1}{d}-\frac{1}{e}=\frac{3}{10} }[/math]을 만족하는 (d,e)는 [math]\displaystyle{ (3,30) }[/math]이다.

각 해에서 면의 수를 구하면 4, 8, 20, 6, 12이다.

정다면체의 확장

정다면체에서 만나는 다각형 조건을 별정다각형을 포함하고, 꼭짓점에서 별모양처럼 만나는 경우를 포함시키면 4개의 정다면체를 더 얻을 수 있다. 이 것을 케플러-푸앵소 다면체라고 부른다.

같이 보기

• 정다포체: 4차원의 정다면체