유수 정리

유수 정리(Residue theorem)는 복소해석학의 적분에 관한 정리이다.

진술

[math]\displaystyle{ \Gamma }[/math]가 단순닫힌 양의 방향의 경로이고 [math]\displaystyle{ f }[/math]가 [math]\displaystyle{ \Gamma }[/math]와 [math]\displaystyle{ \Gamma }[/math]의 [math]\displaystyle{ z_1,\dots, z_n }[/math]을 제외한 내부에서 정칙이라면,

[math]\displaystyle{ \displaystyle \int_\Gamma f(z)dz = 2\pi i\sum_{j=1}^n \operatorname{Res}(f,z_j) }[/math]

이다. 이때 [math]\displaystyle{ \operatorname{Res}(f,z_j) }[/math]는 [math]\displaystyle{ f }[/math]의 [math]\displaystyle{ z=z_j }[/math]에서의 유수이다.

예시

삼각함수가 포함된 적분

[math]\displaystyle{ \displaystyle \int_0^{2\pi} \frac{P(\cos\theta, \cos 2\theta,\dots, \sin \theta, \sin 2\theta, \dots)}{Q(\cos\theta, \cos 2\theta,\dots, \sin \theta, \sin 2\theta, \dots)}d\theta }[/math]

꼴의 적분에 대해 [math]\displaystyle{ z=e^{i\theta} }[/math]로 치환적분을 시도해볼 수 있다.

다음 적분

[math]\displaystyle{ \displaystyle \int_{0}^{2\pi} \frac{e^{in\theta}}{a-\cos\theta}d\theta\quad(a\gt 1) }[/math]

에 대해, [math]\displaystyle{ z=e^{i\theta} }[/math]로 치환하면

[math]\displaystyle{ \displaystyle\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}=\frac{1}{2}\left(z+\frac{1}{z}\right),\quad d\theta=\frac{dz}{iz} }[/math]

이므로

[math]\displaystyle{ \displaystyle \begin{align}\int_{0}^{2\pi} \frac{e^{in\theta}}{a-\cos\theta}d\theta&=\int_C \frac{2z^n}{-i(z^2-2az+1)}dz\\ &=\int_C \frac{iz^n}{(z-z_+)(z-z_-)}dz \end{align} }[/math]

이다. 이때 [math]\displaystyle{ C }[/math]는 양의 방향의 단위원, [math]\displaystyle{ z_\pm=a\pm \sqrt{a^2-1} }[/math]이다. [math]\displaystyle{ C }[/math] 내부에서 [math]\displaystyle{ f(z)=\frac{iz^n}{(z-z_+)(z-z_-)} }[/math]의 극점은 [math]\displaystyle{ z=z_- }[/math]뿐이므로,

[math]\displaystyle{ \displaystyle\int_C \frac{iz^n}{(z-z_+)(z-z_-)}dz= 2\pi i \operatorname{Res}(f,z_-)=\frac{2\pi(a-\sqrt{a^2-1})^n}{\sqrt{a^2-1}} }[/math]

이다. 따라서

[math]\displaystyle{ \displaystyle \int_{0}^{2\pi} \frac{e^{in\theta}}{a-\cos\theta}d\theta =\frac{2\pi(a-\sqrt{a^2-1})^n}{\sqrt{a^2-1}} }[/math]

을 얻는다.

이상적분

[math]\displaystyle{ \displaystyle\int_0^{\infty}\frac{x\sin x}{(1+x^2)^2}dx }[/math]

함수 [math]\displaystyle{ f(z)=\frac{ze^{iz}}{(1+z^2)^2} }[/math]는 [math]\displaystyle{ z=\pm i }[/math]에서 각각 위수 2의 극점을 가짐을 알 수 있다. 이때 양의 방향의 경로 [math]\displaystyle{ \Gamma_R }[/math]을 원점을 중심으로 하고 반지름이 [math]\displaystyle{ R(\gt 1) }[/math]인 반원 [math]\displaystyle{ C_R }[/math]과 시작점이 [math]\displaystyle{ -R }[/math]이고 끝점이 [math]\displaystyle{ R }[/math]인 선분의 합으로 정하면,

[math]\displaystyle{ \displaystyle \int_{\Gamma_R}\frac{ze^{iz}}{(1+z^2)^2}dz=\int_{C_R}\frac{ze^{iz}}{(1+z^2)^2}dz+\int_{-R}^R \frac{xe^{ix}}{(1+x^2)^2}dx }[/math]

이다. [math]\displaystyle{ \Gamma_R }[/math]의 내부에 있는 [math]\displaystyle{ f }[/math]의 극점은 [math]\displaystyle{ z=i }[/math]뿐이므로,

[math]\displaystyle{ \displaystyle \int_{\Gamma_R}\frac{ze^{iz}}{(1+z^2)^2}dz =2\pi i \operatorname{Res}(f,i) = \frac{\pi i}{2e} }[/math]

이다. 한편, 추정 보조정리에 의해

[math]\displaystyle{ \displaystyle \left|\int_{C_R} \frac{ze^{iz}}{(1+z^2)^2}dz\right|\le \pi R\cdot \frac{R}{(R^2-1)^2}\to 0\text{ as }R\to\infty }[/math]

이므로

[math]\displaystyle{ \displaystyle \text{p.v.}\int_{-\infty}^{\infty}\frac{xe^{ix}}{(1+x^2)^2}dx=\frac{\pi i}{2e} }[/math]

이다. 오일러의 공식에 의해

[math]\displaystyle{ \displaystyle \text{p.v.}\int_{-\infty}^{\infty}\frac{x\sin x}{(1+x^2)^2}dx=\frac{\pi}{2e} }[/math]

이고 따라서

[math]\displaystyle{ \displaystyle \int_0^{\infty}\frac{x\sin x}{(1+x^2)^2}dx = \frac{\pi}{4e} }[/math]

이다.

[math]\displaystyle{ \displaystyle\int_0^{\infty} \frac{\sin^2 x}{x^2}dx }[/math]

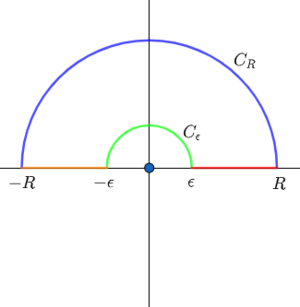
함수 [math]\displaystyle{ f(z)=\dfrac{1-e^{2iz}}{2z^2} }[/math]는 [math]\displaystyle{ z=0 }[/math]에서 단순극점을 가지며, [math]\displaystyle{ \operatorname{Res}(f,0)=-i }[/math]이다. [math]\displaystyle{ 0\lt \epsilon \lt 1 \lt R }[/math]일 때, [math]\displaystyle{ C_R,C_\epsilon }[/math]을 원점을 중심으로 하고 반지름이 각각 [math]\displaystyle{ R,\epsilon }[/math]인 상반원이라 하자. 양의 방향의 경로 [math]\displaystyle{ \Gamma=[\epsilon,R]+C_R+[-R,-\epsilon]+C_\epsilon }[/math]에 대해, [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ \Gamma }[/math] 내부에 극점을 가지고 있지 않다. 따라서

[math]\displaystyle{ \displaystyle \int_\Gamma f(z)dz=0 }[/math]

이다. 한편

[math]\displaystyle{ \displaystyle \int_\Gamma f(z)dz=\left(\int_{\epsilon}^R +\int_{C_R} +\int_{-R}^{-\epsilon} +\int_{C_{\epsilon}} \right)f(z)dz }[/math]

인데, 추정 보조정리에 의해

[math]\displaystyle{ \displaystyle\int_{C_R} f(z)dz\le \pi R\cdot \frac{1+|e^{2iz}|}{R^2}\le \frac{2}{R}\to 0\text{ as }R\to\infty }[/math]

이며, [math]\displaystyle{ z=0 }[/math] 근방에서 [math]\displaystyle{ f }[/math]의 로랑 급수는

[math]\displaystyle{ \displaystyle f(z)=\frac{a_{-1}}{z}+\sum_{n=0}^{\infty} a_n z^n }[/math]

꼴이고

[math]\displaystyle{ \displaystyle\begin{align}\int_{C_\epsilon} f(z)dz&=\int_{C_\epsilon}\frac{a_{-1}}{z}dz+\sum_{n=0}^{\infty}\int_{C_\epsilon} a_n z^n dz\\ &=\int_{\pi}^0 ia_{-1} d\theta +\sum_{n=0}^{\infty} \int_{\pi}^0 a_n \epsilon^n e^{in\theta}\epsilon i e^{i\theta}d\theta \\ &\to -\pi i a_{-1} \text{ as }\epsilon\to 0^+ \end{align} }[/math]

이다. 따라서

[math]\displaystyle{ \displaystyle 0=\text{p.v.}\int_{-\infty}^{\infty} \frac{1-e^{2ix}}{2x^2}dx-\pi ia_{-1} }[/math]

인데, [math]\displaystyle{ a_{-1}=\operatorname{Res}(f,0)=-i }[/math]이고

[math]\displaystyle{ \displaystyle\frac{1-e^{2ix}}{2x^2}=\frac{(1-\cos 2x)-i\sin 2x}{2x^2}=\frac{\sin^2 x}{x^2}-i\frac{\sin 2x}{2x^2} }[/math]

이므로

[math]\displaystyle{ \displaystyle \text{p.v.}\int_{-\infty}^{\infty} \frac{\sin^2 x}{x^2}dx = \pi }[/math]

이다. 따라서

[math]\displaystyle{ \displaystyle \int_0^{\infty} \frac{\sin^2 x}{x^2}dx=\frac{\pi}{2} }[/math]

이다.

[math]\displaystyle{ \displaystyle\int_0^{\infty} \frac{\sqrt{x}}{1+x^2}dx }[/math]

[math]\displaystyle{ \displaystyle\int_0^{\infty} \frac{\ln x}{(x^2+1)(x^2+4)}dx }[/math]

급수의 합

[math]\displaystyle{ \displaystyle\sum_{n=-\infty}^{\infty} f(n)=-\{\text{sum of residues of $\pi\cot(\pi z)f(z)$ at each pole of $f$}\} }[/math]

[math]\displaystyle{ \displaystyle\sum_{n=-\infty}^{\infty} (-1)^n f(n)=-\{\text{sum of residues of $\pi\csc(\pi z)f(z)$ at each pole of $f$}\} }[/math]

양수인 짝수에 대한 리만 제타함수의 함숫값을 구할 수 있다.

[math]\displaystyle{ \displaystyle \zeta(2n)=\sum_{k=1}^{\infty} \frac{1}{k^{2n}} = (-1)^{n-1}B_{2n}\frac{(2\pi)^{2n}}{2(2n)!} }[/math]

이때 [math]\displaystyle{ B_{2n} }[/math]은 베르누이 수이다.

같이 보기

• 조르당의 보조정리
• 편각 원리