오색 정리

진술

오색 정리(Five color theorem)은 임의의 평면그래프를 다섯 가지 색을 이용하여 칠할 수 있다는 명제다. 다시 말해, 평면그래프 G의 색의 개수를 [math]\displaystyle{ \chi(G) }[/math]라 하면,

[math]\displaystyle{ \chi(G)\le 5 }[/math]

이다.

증명

[math]\displaystyle{ \deg v \le 4 }[/math]이면 v에는 언제나 인접한 꼭짓점과 다른 색을 칠하면 된다.

그래프의 모서리의 수 v에 대한 수학적 귀납법으로 증명하려고 한다.

• 기본 단계: [math]\displaystyle{ v=1 }[/math]이면 평면그래프를 한 가지 색을 이용하여 칠할 수 있다.
• 귀납법 단계: [math]\displaystyle{ v=n-1 }[/math]인 평면그래프를 다섯 가지 색을 이용하여 칠할 수 있다고 가정하자. [math]\displaystyle{ v=n }[/math]일 때, 오일러의 다면체 정리에 의하여, 평면그래프 G는 차수가 5 이하인 꼭짓점을 반드시 하나 가진다. 이 꼭짓점을 x라 하자. G에서 x를 제거한 그래프 [math]\displaystyle{ G' = G\setminus x }[/math]의 꼭짓점은 n-1개이므로, G' 는 다섯 가지 색을 이용하여 칠할 수 있다. 따라서 G를 다섯 개 색으로 칠할 수 있음을 보이려면 x를 잘 색칠하면 된다.
  • [math]\displaystyle{ \deg x \le 4 }[/math]일 때, v와 인접한 꼭짓점의 색은 최대 네 가지에 불과하므로, 인접한 꼭짓점의 색이 아닌 걸 골라서 x에 색칠하면 된다.
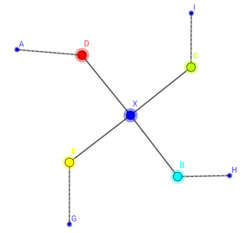
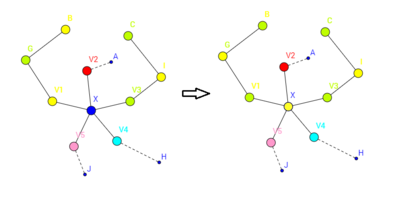
  • [math]\displaystyle{ \deg x =5 }[/math]라고 하자. 이때, x와 인접한 꼭짓점을 시계방향으로 [math]\displaystyle{ v_1,v_2,v_3,v_4,v_5 }[/math]로 지정하고, 색을 1, 2, 3, 4, 5로 부여하자. G' 의 부분그래프 [math]\displaystyle{ G_{1,3} }[/math]을 G' 에서 색이 1과 3인 것을 모두 고르고 모서리로 연결한 그래프라고 하자. 이때 [math]\displaystyle{ G_{1,3} }[/math]에서 v₁에서 v₃로 가는 길이 없다면, v₁의 색을 v₃의 색으로 바꾸고 v₁과 연결된 점의 색 1, 3을 서로 바꾸면 된다. 이때 v₁과 v₃의 색이 모두 3이므로, x를 1로 칠할 수 있다.

음... [math]\displaystyle{ v_2,v_4 }[/math]를 다른 모서리에 닿지 않고 연결하려면 지면을 뚫으면 되겠군그런 거 없다.

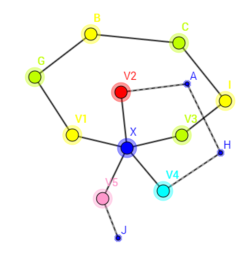
[math]\displaystyle{ G_{1,3} }[/math]에서 v₁에서 v₃로 가는 길이 있다고 하자. 그러면 이제 얘 말고 G' 에서 색이 2와 4인 것을 모두 고르고 모서리로 연결한 그래프인 [math]\displaystyle{ G_{2,4} }[/math]에 대해 생각하자. [math]\displaystyle{ G_{2,4} }[/math]에서 v₂에서 v₄로 가는 길이 없다면 [math]\displaystyle{ G_{1,3} }[/math]의 경우처럼 색을 바꾸면 되는데, v₂에서 v₄로 가는 길이 있다면 G가 평면그래프라는 것에 모순이다! 따라서 [math]\displaystyle{ G_{2,4} }[/math]에서 v₂에서 v₄로 가는 길은 없다. 따라서 G를 다섯 가지 색으로 칠할 수 있으므로 언제나 원하는 결론을 얻는다.

위와 같은 방법을 켐페 사슬이라고 부른다. 알프레드 켐페가 원래 사색 정리의 증명을 발표(?)하면서 쓰인 개념이었으나, 오류가 있음이 발견되었지만 오색 정리를 쉽게 증명하는 등의 다른 곳에 매우 유용함이 알려졌다.

같이 보기

• 사색 정리: 오색 정리보다 강력한 정리로, 임의의 평면그래프는 네 가지 색을 이용해 칠할 수 있다. 1976년에 컴퓨터를 이용해 증명하였다.
• 토마슨의 정리: 오색 정리를 함의하는 또 하나의 정리로, 임의의 고리 없는 평면그래프가 5-선택 가능하다는 정리이다. 채색 수는 언제나 선택 수 이하이므로, 오색 정리가 도출된다.

외부 링크

• Five Color Theorem. (2014, August 13). ProofWiki, . Retrieved 14:39, May 5, 2015.
• Mapa kodów pocztowych - Polska: 폴란드 구역을 다섯 가지 색으로 칠해 보여준다. 2015년 9월 12일 확인.