| 수포자도 쉽게 알 수 있는 수학 | ||||
|---|---|---|---|---|
| 집합과 명제 | 수의 체계와 수의 성질 | 문자와 식 및 방정식과 부등식 | 함수 | 수열 |
| 미분과 적분 | 확률과 통계 | 평면기하학과 공간기하학 | 해석기하학 | |
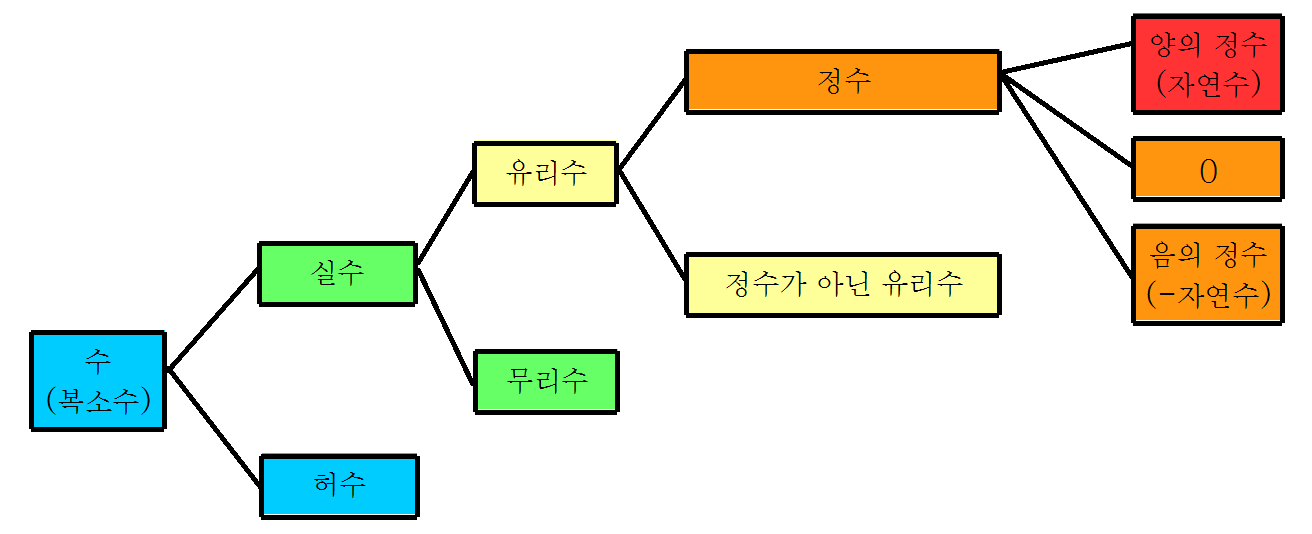
수의 체계[편집 | 원본 편집]
- 자연수(Natural number)는 1, 2, 3, ……과 같이 계속 1씩 늘어나며 이어지는 수이다. 뭐 자연적으로 생각하기 쉬운 수라고 여겨도 상식적으론 문제 없겠다. '자연에 존재하는 수' 라기엔 무리가 있다. 어차피 수는 개념이지 물질이 아니라...[1]
- 사람을 세는 데 쓰는 수라고 생각하면 이해하기 쉽다. 한 사람이면 어른이건 어린이건 1 명이지, 어리다고 ½ 명이라거나 키가 작다고 0.7 명이라 하지는 않는다.
- 좀 더 정확히 말하면 자연수란 개수를 셀 때(= 기수 = 한 명, 두 개, 세 자루, …) 그리고 순위를 나타낼 때(= 서수 = 첫 번째, 두 번째, 세 번째, …) 쓰는 수이다.
- 정수(Integer)는 자연수에 0과 마이너스 자연수(−1, −2, −3, …… 등 −(자연수))를 더한 개념이다. 이때 자연수를 ‘양의 정수’, −(자연수)를 ‘음의 정수’라 한다.
- 유리수(Rational number)는 분수로 나타낼 수 있는 모든 수이다. 물론 분자, 분모가 정수인 분수(설마 분모를 0으로 놓진 않겠지?).
- 실수(Real number)는 수직선 위에 있는 모든 수이다.[2]
- 유리수도 모두 수직선 위에 놓을 수 있지만, 수직선 위에는 유리수가 아닌 수도 존재한다. 대표적인 것이 [math]\displaystyle{ \sqrt{2} }[/math]이다. 이렇게 빠진 부분을 모두 메꾼 것이 바로 실수이다. 따라서 현실 세계의 눈에 보이는 모든 수치는 전부 실수라고 할 수 있다.
- 실수 중 유리수가 아닌 수를 무리수(irrational number)라고 한다(꼭 루트가 있어야 하는 게 아니다).
- 복소수(Complex number)는 a+bi 꼴로 나타낼 수 있는 모든 수이다(a, b는 실수, i는 [math]\displaystyle{ \sqrt{-1} }[/math]). 평면 위에 있는 모든 수라고 생각해도 된다.
- a나 b는 0도 될 수 있으므로 복소수에는 순허수 bi(b≠0)나 실수 a도 포함된다.
- 복소수 중 실수가 아닌 수를 허수(imaginary number)라 한다.
- y=2x+3와 같은 식에서 x나 y는 상황에 따라 달라지므로 변수라 한다. 그러나 3은 변치 않고 항상 일정한 수이므로 상수라 한다. 즉 y=ax+b라고 적어 놓고 “a와 b는 상수”라고 하면, “뭔지 몰라도 2나 3 같이 값이 뭔가로 정해져 있겠구나” 하면 된다.
- 고등학교 과정까지는 아무 언급이 없다면 상수는 실수
mistake이다.
- 고등학교 과정까지는 아무 언급이 없다면 상수는 실수
- 소수(Decimal)[3]란 소수점 아래에 뭔가 값을 갖는 실수이다.
- 유리수를 소수로 나타내면, 0.4(=2/5)이나 0.75(=3/4)처럼 소수점 아래가 가다가 뚝 끝나는 유한소수가 되거나 0.3 45 45 45 …(=19/55)처럼 소수점 아래가 어느 순간부터 계속 반복되는 순환하는 무한소수가 된다. 또한 모든 유한소수 및 순환하는 무한소수는 다 유리수이다.
- 따라서 무리수는 소수로 나타내면 순환하지 않는 무한소수가 되고, 모든 순환하지 않는 무한소수는 무리수이다.
- 무한소수에는 극한의 개념이 녹아 있기 때문에 쉽게 생각하면 안 되고, 오개념만 쌓인다. 제발 부탁하건대 무리수의 개념은 실수 중 유리수가 아닌 수로만 잡고, 무한급수를 제대로 배우기 전까지(=대학교 가기 전까지)는 무한소수 가지고 머리 싸매지 말 것.
수의 성질[편집 | 원본 편집]
정수론[편집 | 원본 편집]
사실 많은 내용이 나오지 않는다. 이 뒤의 심화 내용들이 문제지만.. 정수론은 말 그대로 정수만 가지고 다루는, 정수의 성질을 알아보는 수학...이겠지? 그래서 쉬울까? 절대로 그렇지 않다.
나머지 정리[편집 | 원본 편집]
모든 정수는 다른 정수로 나눈 몫과 나머지를 이용해 나타낼 수 있다. 그런데 그렇게 나타내는 방법은 제수(다른 수를 나누는 수)가 정해지면 유일하다는 것이다.
- 몫과 나머지에 대한 설명 추가바람
예를 들어, 7을 3으로 나눈다고 하자. 그러면 몫은 2, 나머지는 1이다. 따라서, [math]\displaystyle{ 7=3\times 2+1 }[/math]이라고 쓸 수 있다. 그런데 7을 3으로 나눌 때 몫은 2 이외의 값이 안 나오고 나머지도 1 이외의 값이 안 나온다.
이번에는 -12를 5로 나눈다고 하자. 그러면 몫은 -3, 나머지는 3이다. 따라서, [math]\displaystyle{ -12=5\times \left(-3\right)+3 }[/math]이라고 쓸 수 있다. 여기에서 중요한 것은 제수는 항상 자연수이고, 나머지는 0 이상이며 제수보다 작은 정수이다. 나머지를 이렇게 정의하면, 앞서 제시한 예와 마찬가지로 -12를 5으로 나눌 때 몫은 -3 이외의 값이 안 나오고 나머지도 3 이외의 값이 안 나온다.
- F[t]의 나머지 정리와 인수정리에 대한 내용 추가바람
나누어 떨어짐[편집 | 원본 편집]
위의 나머지 정리에서 나머지가 0인 경우이다.
예를 들어, −15 = 5 × (−3)이고 나머지는 0이 된다. 이때 “−15는 5로 나누어 떨어진다”라고 한다. 나중에는 그냥 “5는 −15를 나눈다”라고도 한다.
여기서 배수(multiple)와 약수(divisor)(또는 인수(factor))라는 개념이 등장하는데, a가 c를 나누는 경우 c는 a의 배수, a는 c의 약수(또는 인수)라고 한다. 위의 예에서 −15는 5의 배수이고, 5는 −15의 약수(또는 인수)이다.
0은 모든 수의 배수이고, 1은 모든 수의 약수이다. 또, 수 자기 자신은 항상 자기 자신의 배수이자 약수이다.
최소공배수[편집 | 원본 편집]
두 정수 a, b의 양의 배수들중 겹치는 것들을 공배수(common multiple)라고 한다. 이 중, 특히 가장 작은 공배수를 최소공배수(least common multiple)라고 한다. 예를 들어, 8과 6의 최소공배수는 24이다.
최대공약수[편집 | 원본 편집]
두 정수 a, b의 양의 약수들중 겹치는 것들을 공약수(common divisor)라고 한다. 이 중, 특히 가장 큰 공약수를 최대공약수(great common divisor)라고 한다. 예를 들어, 630과 72의 최대공약수는 18이다.
- 유클리드 호제법
- 두 정수의 최대공약수를 구하는 알고리즘이다. 두 정수 a, b에 대해 a를 b로 나눈 나머지를 r이라고 할 때, a, b의 최대공약수는 b, r의 최대공약수와 같다는 것을 이용한다. 단, 이 때 r은 0이 아니다. a, b의 최대공약수를 gcd(a, b)라고 하면, 위 예제에서 최대공약수는 gcd(630, 72) = gcd(72, 54) = gcd(54, 18) = 18이다.
증명 주의(수포자들의 맨탈을 위하여)
[math]\displaystyle{ g = \operatorname{gcd} \left( a, b \right) }[/math]라고 하자. 그러면 [math]\displaystyle{ g \mid a, b }[/math]이다. [math]\displaystyle{ a = bq + r }[/math]이므로 [math]\displaystyle{ r = a - bq }[/math]인데, [math]\displaystyle{ a, b }[/math]는 [math]\displaystyle{ g }[/math]로 나누어 떨어지므로 [math]\displaystyle{ g \mid r }[/math]이다.
[math]\displaystyle{ a, b, r }[/math]가 모두 [math]\displaystyle{ g }[/math]로 나누어 떨어지므로 [math]\displaystyle{ a = gk, b = gm, r = gn }[/math]([math]\displaystyle{ k, m, n }[/math]은 정수)라고 쓸 수 있다. [math]\displaystyle{ a = bq + r }[/math]의 양 변을 [math]\displaystyle{ g }[/math]로 나누면 [math]\displaystyle{ k = mq + n }[/math]이 된다. [math]\displaystyle{ \operatorname{gcd} \left( k, m \right) }[/math] [math]\displaystyle{ = \operatorname{gcd} \left( mq+n, m \right) }[/math] [math]\displaystyle{ = \operatorname{gcd} \left( n, m \right) = 1 }[/math]이다. 따라서, [math]\displaystyle{ g = \operatorname{gcd} \left( b, r \right) = \operatorname{gcd} \left( a, b \right) }[/math]
소수[편집 | 원본 편집]
어떤 수는 약수가 많고, 어떤 수는 약수가 적다. 그런데 앞서 보았듯 1과 자기 자신은 언제나 자기 자신의 약수이다. 그렇다면 약수의 수가 제일 적은 수는 1과 자기 자신만을 약수로 갖는 수일 것이다. 이런 수를 소수(prime number)라 한다.
잘 알고 있듯이, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, … 이렇게 계속 나아간다.
1은 소수라고 하지 않는다. 모든 수를 나누므로 약수와 배수를 논할 때 의미가 없기 때문이다. 이 말이 좀 이해하기 어려워서 보통은 약수가 1개뿐이기 때문이라고 설명하고, 소수는 ‘약수가 2개뿐인 수’라고 정의하기도 한다.
소수를 알고 있으면 최대공약수, 최소공배수를 구할 때 편하다는 사실은 이미 잘 알고 있을 것이다. 이는 궁극적으로 아래 소인수분해 때문이다.
2는 유일한 짝수인 소수다.
소인수분해[편집 | 원본 편집]
소수인 인수를 소인수라고 한다. 그리고 어떤 수를 소인수들의 곱으로 나타내는 것을 소인수분해라고 한다.
모든 자연수는 소인수분해가 존재하고 유일하다(이 측면에서도 1이 소수이면 곤란하다). 무슨 뜻이냐면, 마음껏 소인수분해를 이용해도 된다는 뜻이다.
배수 판정법[편집 | 원본 편집]
어떤 자연수가 다른 자연수의 배수인지를 알아내는 방법이다. 물론 나눠 보면 된다(…). 하지만 그것보다 쉬운 방법이 있기 때문에 이런 걸 배운다.
소인수분해 때문에 보통은 어떤 소수의 배수인지만 알아내면 된다. 하지만 나누는 수가 소수가 아닌 경우에도 배수 판정법이라고 한다.
- 2n 또는 5n의 배수인지
- 마지막 n 자리만 보면 된다. 이는 10n이 2n 과 5n의 배수이기 때문이다.
- 2n의 경우 10n-1의 자리가 짝수일 경우 10n-2자리 부터는 2n의 배수여야하고, 그렇지 않은 경우 10n-2자리 부터는 2n-1의 배수이면서, 2n의 배수가 아니어야한다.
- 물론 10n의 배수이려면 마지막 n 자리가 전부 0이어야 한다.
- 더 훌륭한 점은 마지막 n 자리를 2n 또는 5n으로 나눈 나머지가 원래 수를 2n 또는 5n으로 나눈 나머지와 같다는 것이다.
- 3n의 배수인지
- n=1의 경우 모든 자릿수(digits)를 다 더해서 3의 배수인지 보면 된다. 이는 10n−1이 3의 배수이기 때문이다.
- 비슷한 이유로 9의 배수인지는 모든 자릿수를 다 더해서 9의 배수인지 보면 된다.
- 노파심에 첨언하자면 6의 배수인 것과 모든 자릿수의 합이 6의 배수인지랑은 관계 없다. 모든 자릿수의 합이 3의 배수이면서 마지막 자리가 짝수이면 된다(…).
- n>2일때 3n의 배수인지 보려면 3n-2자리씩 끊어서 다 더하면 된다. 3과 9의 배수 판정법 및 수학적 귀납법을 통해 증명 가능하다. 예를 들어 111은 3의 배수이고 따라서 999는 103−1이자, 27의 배수이다. 즉, 27의 배수는 3자리씩 끊어 다 더하면 보일 수 있다.
- 이 경우도 3n-2자리씩 끊어서 다 더한 합을 3n으로 나눈 나머지가 원래 수를 3n으로 나눈 나머지와 같다.
- 7의 배수인지
- 7의 배수인지 알고 싶은 어떤 수의 마지막 자릿수를 떼어 두 배를 한 뒤 그 수를 원래 수의 십의 자릿수에서 뺀 것이 7의 배수인지 보면 된다. 즉 10p+q이면 p−2q가 7의 배수인지 보면 된다. 이는 21=3·7이 7의 배수이기 때문이다.
- 달리 말하면 마지막 자리를 떼어 다섯 배를 한 뒤 십의 자리 이상에 더한 것이 7의 배수인지 봐도 된다는 뜻이다. 그런데 상식적으로 덧셈을 하면 숫자가 커지므로 쓸모가 적다.
- 자릿수가 많은 경우 마지막 세 자리를 떼어 천의 자리 이상에서 뺀 것이 7의 배수인지 보기도 한다. 이는 1001=7·11·13이 7의 배수이기 때문이다.
- 참고로 이 경우는 10p+q와 p−2q를 7로 나눈 나머지가 절대로 같지 않다! 주의해야 한다.
- 13의 배수인지도 마지막 세 자리를 떼어 천의 자리 이상에서 빼 봐도 된다.
- 11의 배수인지
- 홀수번째 자릿수(일의 자리, 백의 자리, …)의 합과 짝수번째 자릿수(십의 자리, 천의 자리, …)의 합의 차가 11의 배수인지 보면 된다. 이는 n이 짝수이면 10n−1이, n이 홀수이면 10n+1이 각각 11의 배수이기 때문이다.
- 7의 배수 때와 같이 마지막 세 자리를 떼어 천의 자리 이상에서 빼 봐도 된다.
소수 판정법[편집 | 원본 편집]
어떤 자연수가 소수인지 아닌지를 판별하는 방법이다. 방법은 여러 가지가 있다. 소수 판정법은 현대적으로도 중요한 의미를 갖는다. RSA 암호체계가 소인수분해에 기반하고 있기 때문이다. 여기서 말하는 소수 판정법은 그런 컴퓨터를 이용해야 할 만한 본격적인 방법 말고, 닝겐의 힘으로 소수인지 아닌지 판별하는 방법을 말한다. 본질적으로 배수 판정법이 필요하다.
사실, 소수는 정수론의 난제이다. 괜히 고독한 인간에게 힘을 주는 게 아니다. 예를 들어 '소수 공식'이 있다고 쳐서
어떤 정수를 넣으면 소수인지 아닌지 판단 가능하다고 하면, 인간은 소수를 정복한 거다. 계산이 복잡하면 컴퓨터 시키면 되고. 수열이나 함수를 봐도 하나같이 n항, y = 2x+1 처럼 보편적인 식을 구하지 않는가? 이러면 어떤 상황에도 적용할 수 있다. 그런데 소수는 위에서 말한 '소수 공식', 수열이나 함수로 따지면 일반항, 보편적인 식이 구해지지 않았다. 그러니까 밑에 나온 방법은 꼼수를 쓰긴 했지만 본질적으로 노가다다(될 때까지 나눠보는).
에라토스테네스의 체[편집 | 원본 편집]
일정 범위(예를 들어 2 이상 100 이하)의 자연수를 소수와 합성수로 싹 갈라 넣는 방법이다.
2 이상 N 이하의 자연수를 쭉 나열해 놓고(규칙적으로 직사각형 모양으로 나열하면 좋다), 다음과 같은 알고리즘을 반복한다.
i) ○표나 ✕표가 쳐져 있지 않은 최소의 자연수에 ○표를 한다. → 소수
ii) i)에서 표기한 자연수의 배수에 ✕표를 한다. → 합성수
iii) 모든 자연수에 ○표나 ✕표가 쳐졌다면 종료한다. 아니라면 i)로 돌아간다.
이 방법은 일정 범위 내에 있는 모든 소수를 찾아낼 수 있다는 점이 장점이다. 그러나 일단 자연수를 전부 나열해야 되고 전부 나열하자마자 그 중 절반(짝수)을 죽죽 지우면서 내가 왜 이걸 했지 하게 되는 등 시간적·공간적으로 번잡한 면이 있다.
2 이상 [math]\displaystyle{ \sqrt{n} }[/math] 이하의 소수로 나눠 보는 방법[편집 | 원본 편집]
어떤 정해진 자연수 n 딱 하나가 소수인지를 판별하기 위해 에라토스테네스의 체를 사용하기는 낭비이다. 이때는 2 이상 n 미만의 자연수 중 n을 나누는 수가 있는지를 보면 된다.
그런데, 사실 [math]\displaystyle{ n }[/math]이 합성수라면 [math]\displaystyle{ \sqrt{n} }[/math] 이하의 소인수를 최소한 하나는 반드시 갖기 때문에, 결론적으로 2 이상 [math]\displaystyle{ \sqrt{n} }[/math] 이하의 소수로만 나눠 보면 된다.
증명은 간단하다.
수식 주의
[math]\displaystyle{ n }[/math]이 합성수라면 자기 자신이 아닌 소인수를 가질 것이다. 아무 거나 하나 잡아 [math]\displaystyle{ q }[/math]라고 하자.
(i) 만일 [math]\displaystyle{ q \leq \sqrt{n} }[/math]이면 끝.
(ii) 아니라면 [math]\displaystyle{ \frac{n}{q} \lt \sqrt{n} }[/math]일 것이므로 [math]\displaystyle{ \frac{n}{q} }[/math]의 소인수를 아무 거나 하나 잡으면 끝.
쪼개기[편집 | 원본 편집]
위 방법을 쓰려고 해도, 예를 들어 691이 소수인지 알아보기 위해서는 2부터 23까지 9개의 소수로 나눠 봐야 한다. 이것도 너무 귀찮은 경우 수를 적당히 쪼개서 소수를 두어 개씩 세트로 날릴 수 있다.
이 방법은 작은 수의 배수 판정이 쉽다는 점을 이용한 것이다.
계속 691로 예를 들자.
- 일단 2나 5의 배수는 아니다.
2357 11 13 17 19 23
- 690과 1로 쪼갠다.
- 690=3·23·10인데 1은 3의 배수도 23의 배수도 아니므로 691은 3이나 23의 배수가 아니다.
2 3 57 11 13 17 1923
- 600과 91로 쪼갠다.
- 91=7·13인데 600은 7의 배수도 13의 배수도 아니므로 691은 7이나 13의 배수가 아니다.
2 3 5 7111317 1923
- 680과 11로 쪼갠다.
- 680은 11의 배수가 아니므로 691은 11의 배수가 아니다.
- 680=4·17·10인데 11은 17의 배수가 아니므로 691은 17의 배수가 아니다.
2 3 5 7 11 13 171923
- 570과 121로 쪼갠다.
- 570=3·19·10인데 121=112는 19의 배수가 아니므로 691은 19의 배수가 아니다.
2 3 5 7 11 13 17 19 23
(어떻게 570과 121로 쪼갤 생각을 했냐고? 이 방법은 본질적으로 나눗셈이다. 691을 19로 나누어 보려면, 먼저 몫의 십의 자리에 3을 적고 십의 자리에서 57을 빼서 121로 만들 것이다. 그런데 여기서 더 진행하지 않고, 121=112이라는 사실만으로 끝낸 것이다.)
따라서 네 번만에 691이 소수임을 알게 되었다.
소인수분해[편집 | 원본 편집]
임의의 자연수 [math]\displaystyle{ n }[/math]을 소수들만의 곱으로 나타내는 것이다. 위에 서술한 소수판정법을 이용해서 자기 자신과 1이 아닌 인수가 발견될 경우, 자기 자신을 인수로 나누는 과정을 소수만 남을 때까지 반복한다. 그 다음, 그 때까지 구한 인수들 중 소수가 아닌 인수들에 대해 같은 과정을 반복하면 된다.뭐래는겨
이게 무슨 소리인지 예제를 통해 확인해보자. 780을 소인수분해 한다고 해보자. 우선적으로, 2와 5로 나누는 것을 시도해서 [math]\displaystyle{ 780=2^2\times 5\times 39 }[/math]를 얻고, [math]\displaystyle{ 39=3\times 13 }[/math]이므로 최종적으로 [math]\displaystyle{ 780=2^2\times 3\times 5\times 13 }[/math]을 얻는다.
정수 함수[편집 | 원본 편집]
흔히들 '가우스 함수'라고 부르는 그것이다. 사실 가우스 함수는 따로 이르는 것이 있으며, 정수 함수, 또는 바닥 함수(floor function), 버림 함수가 옳은 표현이다. 어떤 실수 [math]\displaystyle{ x }[/math]에 대해 정수 [math]\displaystyle{ n }[/math]이 존재하여 [math]\displaystyle{ n\le x \lt n+1 }[/math]를 만족할 때, [math]\displaystyle{ \lfloor x\rfloor=n }[/math]으로 정의한다. 즉 [math]\displaystyle{ x }[/math]의 정수부(integer part)만을 가져오는 함수이다. 비슷하게 소수부만을 가져오는 함수도 있으며, [math]\displaystyle{ \{x\}=x-\lfloor x\rfloor }[/math]로 표현한다. 이는 집합, 수열과 표기하는 기호가 같아 잘 쓰이지 않는다.
이는 수의 어림에서 배웠던 버림 단항연산의 함수 형태이다. 버림 연산 말고도 반올림(사사오입, round function) [math]\displaystyle{ (x)=\left\lfloor x + \frac 1 2 \right\rfloor }[/math], 올림(ceiling function) [math]\displaystyle{ \lceil x \rceil = n \text{ s.t. }n\lt x \le n+1 }[/math] 등이 있다.
절댓값[편집 | 원본 편집]
절댓값의 정의는 어떤 수를 수직선에 표시했을 때 원점(0)에서부터의 거리인데, 그냥 부호만 빼면 된다. 4의 절대값은 4이고 -3의 절댓값은 3이 된다. 단, 이해는 그냥 부호만 뺀다기 보다 -부호를 한번 더 붙혀 양수를 만든다고 생각하는 것이 문자의 절댓값 표시 에서 더 헷갈리지 않는다. 즉, 4의 절댓값은 4, -3의 절댓값은 -(-3)=3이다.
복소수[편집 | 원본 편집]
모든 복소수는 [math]\displaystyle{ a+bi(a, b는 실수) }[/math]형태로 나타낼 수 있는데, 이 복소수의 허수부의 부호를 바꾼 수([math]\displaystyle{ a-bi }[/math])를 켤레복소수라고 한다.
각주
| 쉽게 알 수 있는 학문 | |
|---|---|
| 쉽게 할 수 있는 취미 | |
| 창작 안내서 시리즈 | |
| 뭘헤매지 시리즈 | |
| 여행 시리즈 | |
| 연표 시리즈 | |
| 생활의 지혜 | |
| 리브레 기네스 | |
| 리브레 위키 | |
| 기타 | |