라플라스 변환

정의

[math]\displaystyle{ 0\le t\lt \infty }[/math]에서 정의된 함수 f에 대해,

[math]\displaystyle{ \displaystyle F(s)=\mathcal{L}(f(t))=\int_0^{\infty}f(t)e^{-st}dt\quad(s\in \mathbb{C}) }[/math]

를 f(t)의 라플라스 변환(Laplace transform), 또는 단방향 라플라스 변환(Unilateral laplace transform)이라 한다. 그러면 "양방향"도 있을 것 같은데, 실제로 쓰고 있다.
함수가 [math]\displaystyle{ -\infty\lt t\lt \infty }[/math]에서 정의되어 있을 때,

[math]\displaystyle{ \displaystyle \mathcal{B}(f(t))=\int_{-\infty}^{\infty}e^{-st}f(t)dt }[/math]

를 양방향 라플라스 변환(Bilateral laplace transform)이라 한다. 이 문서에서는 단방향 라플라스 변환에 대해서만 다룬다.

미분방정식을 푸는 매우 강력한 방법으로, 쉽게 설명하자면, t에 대한 함수의 미분방정식을 라플라스 변환하여 s에 관한 식으로 만들고, 간단한 대수적 계산을 이용해 정리한 뒤에 해당 식을 라플라스 역변환을 해주면 간편하게 미분방정식의 해를 구할 수 있다. 라플라스 역변환도 따로 존재하긴 하지만, 하단에 서술되어 있지만 매우 복잡할 뿐더러 복소해석학이 동원되는 이유로 보통은 여러 함수의 라플라스 변환을 정리해놓은 표를 토대로 역변환 결과를 추론해내는 방법을 쓴다.

존재성

라플라스 변환이 언제나 존재하는 것은 아니다. 예를 들어 [math]\displaystyle{ f(t)=e^{t^2} }[/math]라면

[math]\displaystyle{ \displaystyle F(s)=\int_0^{\infty}e^{t^2-st}dt=\infty }[/math]

이므로 f의 라플라스 변환은 존재하지 않는다. 함수 f에 대해 양수 M, t₀와 실수 α가 존재하여 임의의 t≥t₀에 대해

[math]\displaystyle{ |f(t)|\le M e^{\alpha t} }[/math]

를 만족하면 f는 지수적 차수(exponential order) α를 가진다고 한다. 만약 f가 [math]\displaystyle{ [0,\infty) }[/math]에서 조각적 연속이고 지수적 차수 α를 가진다면, f의 라플라스 변환은 [math]\displaystyle{ \operatorname{Re}s \gt \alpha }[/math]에서 존재하고 절대수렴한다. 단, 역은 성립하지 않는다. 예를 들어 [math]\displaystyle{ f(t)=\ln t }[/math]는 [math]\displaystyle{ [0,\infty) }[/math]에서 조각적 연속이 아니지만

[math]\displaystyle{ \displaystyle \mathcal{L}(\ln t)=-\frac{\ln s +\gamma}{s} }[/math]

이다. 이때 γ는 오일러-마스케로니 상수다.

유일성

어떤 라플라스 변환에 대응되는 함수는 일반적으로 유일하지 않다. 예를 들어, 함수 f, g를 다음과 같이 정의하자.

[math]\displaystyle{ f(t)=e^{-t} }[/math]

[math]\displaystyle{ g(t)=\begin{cases} e^{-t} & (0\le x \lt 1, 1\lt x\lt \infty)\\ 1 & (x= 1) \end{cases} }[/math]

그러면 [math]\displaystyle{ F(s)=G(s)=\dfrac{1}{s+1} }[/math]이다. 따라서 [math]\displaystyle{ H(s)=\dfrac{1}{s+1} }[/math]인 함수 h는 유일하지 않다. 이 결과는 라플라스 변환을 기껏 정의해놓고서 못 쓰는 건 아닌가 하는 불안을 불러일으킨다. 다행히 역라플라스 변환으로 (조각적) 연속함수를 찾는다면 그 연속함수는 유일하기 대문에 걱정하지 않아도 된다. 다시 말하면, 정의역이 [math]\displaystyle{ [0,\infty) }[/math]인 연속함수 f,g에 대해 [math]\displaystyle{ F(s)=G(s) }[/math]이면 f=g이다. 더 나아가, 정의역이 [math]\displaystyle{ [0,\infty) }[/math]인 조각적 연속함수 f,g에 대해 [math]\displaystyle{ F(s)=G(s) }[/math]이면 불연속인 점을 제외했을 때 f=g이다.

역라플라스 변환

[math]\displaystyle{ F(s)=\mathcal{L}(f(t)) }[/math]이면 f(t)를 F(s)의 역라플라스 변환(Inverse laplace transformation)이라고 한다. 만약 f가 [math]\displaystyle{ [0,\infty) }[/math]에서 연속이고 t<0일 때 f(t)=0이며, 지수적 차수 α를 가지고 f' 가 [math]\displaystyle{ [0,\infty) }[/math]에서 조각적 연속이면, 역라플라스 변환은 다음 공식으로 나타낼 수 있다.

[math]\displaystyle{ \displaystyle f(t)=\lim_{y\to\infty}\frac{1}{2\pi i}\int_{x-iy}^{x+iy}e^{ts}F(s)ds }[/math] (푸리에-멜린 반전공식)

그런데 이 공식을 잘 쓰려면 유수 정리 같은 복소함수론의 정리를 잘 이용해야 하므로 복소함수론을 배우지 않았으면 이 공식 대신 라플라스 변환표에서 변환에 맞는 함수를 찾아서 쓴다. 적분을 직접 하고 싶다? 직접 해보자. 어떤 연속함수 f의 라플라스 변환이 다음과 같이 주어졌다고 하자.

[math]\displaystyle{ \displaystyle F(s)=\frac{2as}{(s^2+a^2)^2} }[/math]

그림은 복소함수의 경로적분 설정. 푸리에-멜린 반전공식 하나를 이용하기 위해 적분경로를 설정하고 유수 정리를 활용해야 한다. 학부 수준에서 쓸 만한 역변환은 표에 거의 다 나와 있으므로, 차라리 그걸 외우자.

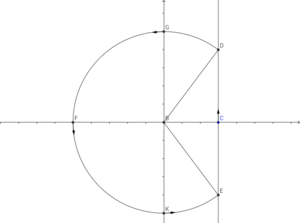
그러면 [math]\displaystyle{ F(s) }[/math]는 [math]\displaystyle{ s=\pm ai }[/math]에서 이차극점을 가진다. 이때 그림과 같이 복소평면 위에 점 (x,0)을 지나고 허수축과 평행인 직선 ED와, 원점을 중심으로 하고 경로가 DGFKE인 부분원 [math]\displaystyle{ C_R }[/math]을 생각하자. 이때 [math]\displaystyle{ R^2=x^2+y^2 }[/math]이다. [math]\displaystyle{ R\gt a }[/math]이 되도록 충분한 R을 설정할 수 있고, 이때 극점 [math]\displaystyle{ \pm ai }[/math]는 닫힌 경로 EDGFKE의 내부에 속한다. 이때 이 경로를 [math]\displaystyle{ \Gamma }[/math]라고 하자. 그러면

[math]\displaystyle{ \displaystyle \int_{\Gamma}e^{ts}F(s)ds=\int_{ED}e^{ts}F(s)ds+\int_{C_R}e^{ts}F(s)ds }[/math]

이다. 이때

[math]\displaystyle{ \displaystyle \lim_{R\to\infty}\int_{C_R}e^{ts}F(s)ds=0 }[/math]

이고 유수 정리에 의해

[math]\displaystyle{ \displaystyle \int_{\Gamma}e^{ts}F(s)ds=2\pi i(\operatorname{Res}(ai)+\operatorname{Res}(-ai)) }[/math]

이다. 계산을 열심히 하면

[math]\displaystyle{ \displaystyle \operatorname{Res}(ai)=-\frac{1}{2}ite^{iat},\quad \operatorname{Res}(-ai)=\frac{1}{2}ite^{-iat} }[/math]

이므로

[math]\displaystyle{ \displaystyle \begin{align}\int_{\Gamma}e^{ts}F(s)ds&=2\pi i\left(-\frac{1}{2}ite^{iat}+\frac{1}{2}ite^{-iat} \right)\\ &=2\pi i t\left(\frac{e^{iat}-e^{-iat}}{2i}\right)\\ &=2\pi i t\sin at \end{align} }[/math]

이다. 이 식을 푸리에-멜린 반전공식에 대입하면

[math]\displaystyle{ f(t)=t\sin at }[/math]

를 얻는다. 그런데 이거 라플라스 변환표에 기본적으로 나와 있는 것이므로, 꼭 필요한 때가 아니라면 이 문서처럼 쓸데없이 길게 적분하지 말고 변환표 외우자.

성질

[math]\displaystyle{ \mathcal{L}(f_1(t))=F_1(s),\mathcal{L}(f_2(t))=F_2(s) }[/math]

원함수	변환	수렴영역
1. [math]\displaystyle{ \mathcal{L}(c_1 f_1(t)+c_2f_2(t)) }[/math]	[math]\displaystyle{ c_1F_1(s)+c_2F_2(s) }[/math]
2. [math]\displaystyle{ \mathcal{L}(f^{(n)}(t)) }[/math]	[math]\displaystyle{ s^n\mathcal{L}(f(t))-s^{n-1}f(0)-\cdots-f^{(n-1)}(0) }[/math]
3. [math]\displaystyle{ \mathcal{L}(t^n f(t)) }[/math]	[math]\displaystyle{ (-1)^n F^{(n)}(s) }[/math]
4.[math]\displaystyle{ L\left\{e^{at}f\left(t\right)\right\} }[/math]	[math]\displaystyle{ F\left(s-a\right) }[/math]
5. [math]\displaystyle{ L\left\{\frac{f\left(t\right)}{t}\right\} }[/math]	[math]\displaystyle{ \int_{s}^{\infty}F\left(u\right)du }[/math]
6. [math]\displaystyle{ \mathcal{L}\left(\int_0^t f(u)du\right) }[/math]	[math]\displaystyle{ \frac{F(s)}{s} }[/math]
7. [math]\displaystyle{ f(t+T)=f(t) }[/math]	[math]\displaystyle{ \dfrac{\int_0^T e^{-st}f(t)dt}{1-e^{sT}} }[/math]
8. [math]\displaystyle{ \mathcal{L}\left\{f*g\right\} }[/math]	[math]\displaystyle{ F(s)G(s) }[/math]
참고사항. [math]\displaystyle{ (f * g)(t)=\int_0^{\tau} f(\tau)g(t - \tau)d\tau }[/math]는 합성곱.

증명

1. 적분의 성질에 의해 쉽게 증명할 수 있다.

2. [math]\displaystyle{ \mathcal{L}\left\{f'\left(t\right)\right\}=\int_{0}^{\infty}e^{-st}f'\left(t\right)dt = \left[e^{-st}f\left(t\right)\right]_{0}^{\infty} + \int_{0}^{\infty}se^{-st}f\left(t\right)dt = sF\left(s\right) - f\left(0\right) }[/math] (부분적분)

위를 반복하면 된다.

3. [math]\displaystyle{ F\left(s\right) = \int_{0}^{\infty}e^{-st}f\left(t\right)dt }[/math] [math]\displaystyle{ F'\left(s\right) = \int_{0}^{\infty}e^{-st}\left(-tf\left(t\right)\right)dt = \mathcal{L}\left\{-tf\left(t\right)\right\} }[/math]

위를 반복하면 된다.

4.[math]\displaystyle{ \mathcal{L}\left\{e^{at}f\left(t\right)\right\} = \int_{0}^{\infty}e^{-st}e^{at}f\left(t\right)dt = \int_{0}^{\infty}e^{-\left(s-a\right)}f\left(t\right)dt = F\left(s-a\right) }[/math]

5. [math]\displaystyle{ \int_{s}^{\infty}F\left(u\right)du = \int_{s}^{\infty}\int_{0}^{\infty}e^{-ut}f\left(t\right)dtdu = \int_{0}^{\infty}\int_{s}^{\infty}e^{-ut}f\left(t\right)dudt = }[/math]
[math]\displaystyle{ \int_{0}^{\infty}f\left(t\right)\int_{s}^{\infty}e^{-ut}dudt = \int_{0}^{\infty}\frac{1}{t}e^{-st}f\left(t\right)dt = L\left\{\frac{f\left(t\right)}{t}\right\} }[/math]

푸비니의 정리를 사용하며, 함수 [math]\displaystyle{ f\left(t\right) }[/math]의 라플라스 변환과 [math]\displaystyle{ \lim_{t \to 0}\frac{f\left(t\right)}{t} }[/math]가 존재한다는 가정이 필요하다.

8. [math]\displaystyle{ \mathcal{L}\left\{f*g\right\}=\int_{0}^{\infty}e^{-st}\int_{0}^{t}f\left(t-u\right)g\left(u\right)dudt = \int_{0}^{\infty}\int_{u}^{\infty}e^{-su}g\left(u\right)e^{-s\left(t-u\right)}f\left(t-u\right)dtdu = }[/math]
[math]\displaystyle{ \int_{0}^{\infty}e^{-su}g\left(u\right)\int_{u}^{\infty}e^{-s\left(t-u\right)}f\left(t-u\right)dtdu }[/math]
[math]\displaystyle{ \xi = t-u }[/math]라 치환하면, [math]\displaystyle{ \int_{0}^{\infty}e^{-su}g\left(u\right)\int_{0}^{\infty}e^{-s\xi}f\left(\xi\right)d\xi du=F(s)G(s) }[/math]
적분 순서의 변경과 푸비니의 정리를 사용한다.

라플라스 변환표

공업수학에서 필수적으로 이 관련 표가 나온다. 적어도 이 표는 죄다 외워주는 게 시험보기 편하다. 잘 못외우면 [math]\displaystyle{ e^t }[/math]의 변환이 [math]\displaystyle{ \frac{1}{s-1} }[/math]이라는 것을 외우고, 이걸 더하고 빼고 해서 삼각함수 쪽은 다 직접 유도할 수 있긴 하다. 하지만 역시 외우는 게 편하다.

이걸 어떻게 다 외워? 살려줘~~

[math]\displaystyle{ f(t) }[/math]	[math]\displaystyle{ \mathcal{L}(f) }[/math]	수렴영역
1	[math]\displaystyle{ \frac{1}{s} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ t^p }[/math] (단, p>-1)	[math]\displaystyle{ \frac{\Gamma(p+1)}{s^{p+1}} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ \sin(at) }[/math]	[math]\displaystyle{ \frac{a}{s^2+a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ \cos(at) }[/math]	[math]\displaystyle{ \frac{s}{s^2+a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ t\sin(at) }[/math]	[math]\displaystyle{ \frac{2as}{(s^2+a^2)^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ t\cos(at) }[/math]	[math]\displaystyle{ \frac{s^2-a^2}{(s^2+a^2)^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ \sinh(at) }[/math]	[math]\displaystyle{ \frac{a}{s^2-a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt |a| }[/math]
[math]\displaystyle{ \cosh(at) }[/math]	[math]\displaystyle{ \frac{s}{s^2-a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt |a| }[/math]
[math]\displaystyle{ t\sinh(at) }[/math]	[math]\displaystyle{ \frac{2as}{(s^2-a^2)^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt |a| }[/math]
[math]\displaystyle{ t\cosh(at) }[/math]	[math]\displaystyle{ \frac{s^2+a^2}{(s^2-a^2)^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt |a| }[/math]
[math]\displaystyle{ e^{at} }[/math]	[math]\displaystyle{ \frac{1}{s-a} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ e^{at}\sin(bt) }[/math]	[math]\displaystyle{ \frac{b}{(s-a)^2+b^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ e^{at}\cos(bt) }[/math]	[math]\displaystyle{ \frac{s-a}{(s-a)^2+b^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ t^n e^{at} }[/math] (단, n은 자연수)	[math]\displaystyle{ \frac{n!}{(s-a)^{n+1}} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ H_c(t) }[/math] (단, c>0)	[math]\displaystyle{ \frac{e^{-cs}}{s} }[/math]
[math]\displaystyle{ \delta_c(t) }[/math] (단, c>0)	[math]\displaystyle{ e^{-cs} }[/math]
참고사항. [math]\displaystyle{ \Gamma(t) }[/math]는 감마함수. [math]\displaystyle{ H_c(t) }[/math]는 헤비사이드 함수. (단위 계단 함수 라고도 한다.) [math]\displaystyle{ \delta_c(t) }[/math]는 디랙 델타 함수.

이걸 어떻게 다 외워? 살려줘~~

다른 변환과의 관계

푸리에 변환

푸리에 변환은

[math]\displaystyle{ \mathcal{F}(f(t))=\hat{f}(\xi)=\int_{-\infty}^{\infty}f(t)e^{-2\pi i t \xi}dt\quad(\xi\in\mathbb{R}) }[/math]

로 주어지는데, 붕괴인자(Decaying factor) [math]\displaystyle{ e^{-\sigma t}\;(\sigma\in\mathbb{R}) }[/math]를 곱하면 주어진 변환은

[math]\displaystyle{ \int_{-\infty}^{\infty}f(t)e^{-\sigma t-2\pi i t \xi}dt\quad(\xi\in\mathbb{R}) }[/math]

이고 [math]\displaystyle{ s=\sigma+2\pi i \xi }[/math]로 두면

[math]\displaystyle{ \int_{-\infty}^{\infty}f(t)e^{-st}dt }[/math]

이고, 이 식은 양방향 라플라스 변환과 동일하다. t<0일 때 [math]\displaystyle{ f(t)=0 }[/math]라고 하면,

[math]\displaystyle{ \int_0^{\infty}f(t)e^{-st}dt }[/math]

이 되므로 라플라스 변환이 된다. 따라서 다음 식이 성립한다.

[math]\displaystyle{ \mathcal{F}(f(t)e^{-\sigma t})=\mathcal{L}(f(t)) }[/math]

활용

미분방정식의 풀이

미분방정식 교재 여럿이 이계 미분방정식을 푸는 방법으로 라플라스 변환을 도입한다. 미분방정식

[math]\displaystyle{ \frac{d^2x}{dt^2}+2\beta \frac{dx}{dt}+w_0^2 x = 0 }[/math]

이 주어졌다고 하자. 이때 양변의 라플라스 변환은

[math]\displaystyle{ (s^2F(s)-sf(0)-f'(0))+2\beta(sF(s)-f(0))+w_0^2F(s)=0 }[/math]

이고, 식을 F(s)에 대해 나타내면

[math]\displaystyle{ F(s)=\dfrac{(s+2\beta)f(0)+f'(0)}{s^2+2\beta s +w_0^2}=\frac{(s+\beta)f(0)}{s^2+2\beta s +w_0^2}+\frac{\beta f(0)+f'(0)}{s^2+2\beta s +w_0^2} }[/math]

이다. [math]\displaystyle{ F_1(s),F_2(s) }[/math]를 다음과 같이 정의하자.

[math]\displaystyle{ F_1(s)=\frac{(s+\beta)f(0)}{s^2+2\beta s +w_0^2} }[/math]

[math]\displaystyle{ F_2(s)=\frac{\beta f(0)+f'(0)}{s^2+2\beta s +w_0^2} }[/math]

[math]\displaystyle{ w_0^2\gt \beta^2 }[/math]라고 가정하자. 그러면

[math]\displaystyle{ F_1(s)=f(0)\frac{s+\beta}{(s+\beta)^2+(\sqrt{w_0^2-\beta^2})^2}=f(0)\mathcal{L}(e^{-\beta t}\cos(\sqrt{w_0^2-\beta^2}t)) }[/math]

[math]\displaystyle{ F_2(s)=\frac{\beta f(0)+f'(0)}{\sqrt{w_0^2-\beta^2}}\frac{\sqrt{w_0^2-\beta^2}}{(s+\beta)^2+(\sqrt{w_0^2-\beta^2})^2}=\frac{\beta f(0)+f'(0)}{\sqrt{w_0^2-\beta^2}}\mathcal{L}(e^{-\beta t}\sin(\sqrt{w_0^2-\beta^2}t)) }[/math]

따라서

[math]\displaystyle{ x(t)=f(0)e^{-\beta t}\cos(\sqrt{w_0^2-\beta^2}t)+\frac{\beta f(0)+f'(0)}{\sqrt{w_0^2-\beta^2}}\cdot e^{-\beta t}\sin(\sqrt{w_0^2-\beta^2}t) }[/math]

를 얻는다.어때요, 정말 쉽죠?

이외에 편미분방정식을 푸는 데도 라플라스 변환이 유용하게 쓰일 수 있다.

[math]\displaystyle{ y=y(x,t)\;(t\gt 0) }[/math]

이고 t를 시간 변수라 하면, y에 대한 라플라스 변환 [math]\displaystyle{ U(x,s) }[/math]는

[math]\displaystyle{ U(x,s)=\int_0^{\infty}e^{-st}y(x,t)dt }[/math]

이다.

편미분방정식

[math]\displaystyle{ \frac{\partial y}{\partial x}+\frac{1}{x}\frac{\partial y}{\partial t}=t,\quad x\gt 0,t\gt 0. }[/math]

[math]\displaystyle{ y(x,0^+)=x,\quad y(0,t)=0 }[/math]

를 라플라스 변환을 이용해 풀어보자. 양변에 라플라스 변환을 적용하면

[math]\displaystyle{ \mathcal{L}\left(\frac{dy}{dx}\right)=\frac{dU(x,s)}{dx},\quad\mathcal{L}\left(\frac{dy}{dt}\right)=sU(x,s)-y(x,0^+) }[/math]

이므로

[math]\displaystyle{ \frac{dU(x,s)}{dx}+\frac{1}{x}(sU(x,s)-y(x,0^+))=\frac{1}{s^2} }[/math]

이고 정리하면

[math]\displaystyle{ \frac{dU(x,s)}{dx}+\frac{s}{x}U(x,s)=1+\frac{1}{s^2} }[/math]

이다. 그러면

[math]\displaystyle{ \frac{d}{dx}(x^s U(x,s))=x^s\left(1+\frac{1}{s^2}\right) }[/math]

이므로

[math]\displaystyle{ U(x,s)=\left(1+\frac{1}{s^2}\right)\frac{1}{s+1}x+Cx^{-s} }[/math]

이다. [math]\displaystyle{ \mathcal{L}(y(0,t))=0 }[/math]이다. 그러므로 [math]\displaystyle{ x\to0^+ }[/math]일 때

[math]\displaystyle{ 0=\lim_{x\to0^+}Cx^{-s} }[/math]

이기 때문에 [math]\displaystyle{ C=0 }[/math]을 얻는다. 따라서

[math]\displaystyle{ U(x,s)=\left(1+\frac{1}{s^2}\right)\frac{1}{s+1}x }[/math]

이므로 열심히 조작하면

[math]\displaystyle{ U(x,s)=\left(\frac{2}{s+1}-\frac{1}{s}+\frac{1}{s^2}\right)x }[/math]

이다. 따라서

[math]\displaystyle{ y(x,t)=(2e^{-t}-1+t)x }[/math]

을 얻는다.

이상적분의 계산

라플라스 변환을 이용하면 부정적분이 초등함수로 나타나지 않는 함수의 이상적분을 계산할 수 있다. 이상적분

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-x}-e^{-2x}}{x}dx }[/math]

를 계산해보자. [math]\displaystyle{ f(x)=\dfrac{e^{-x}-e^{-2x}}{x} }[/math]라 하면 [math]\displaystyle{ xf(x)=e^{-x}-e^{-2x} }[/math]이다. f의 라플라스 변환을 F(s)라 하면 F(s)는 [math]\displaystyle{ s\gt -1 }[/math]일 때 존재하고

[math]\displaystyle{ - \frac{dF(s)}{ds}=\frac{1}{s+1}-\frac{1}{s+2} }[/math]

이다. 정리하면

[math]\displaystyle{ F(s)=\ln(s+2)-\ln(s+1) }[/math]

을 얻는다. 따라서

[math]\displaystyle{ \ln(s+2)-\ln(s+1)=F(s)=\int_0^{\infty}e^{-sx}\frac{e^{-x}-e^{-2x}}{x}dx }[/math]

이며, [math]\displaystyle{ s=0 }[/math]을 대입하면

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-x}-e^{-2x}}{x}dx=\ln 2 }[/math]

를 얻는다. 일반적으로

[math]\displaystyle{ \mathcal{L}\left(\frac{f(t)}{t}\right)=\int_s^{\infty}F(u)du }[/math]

이므로 라플라스 변환의 정의에 의해

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-st}f(t)}{t}dt=\int_s^{\infty}F(u)du }[/math]

이고, 수렴영역이 [math]\displaystyle{ s\gt a }[/math]이면 [math]\displaystyle{ s\to a+ }[/math]일 때

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-at}f(t)}{t}dt=\int_a^{\infty}F(u)du }[/math]

를 얻는다.

점화식의 일반항 계산

라플라스 변환을 이용해 점화식으로 주어진 수열의 일반항을 구할 수 있다.

[math]\displaystyle{ \mathcal{L}(a^{\lfloor t \rfloor})=\frac{1-e^{-s}}{s(1-ae^{-s})} }[/math]

임을 이용하여 점화식

[math]\displaystyle{ a_{n+2}-a_{n+1}-a_n=0,\;a_0=0,\;a_1=1 }[/math]

으로 주어진 피보나치 수열의 일반항을 구해보자. 함수 f를

[math]\displaystyle{ f(t)=a_n\quad(n\le t\lt n+1) }[/math]

로 정의하자. 그러면 주어진 점화식은

[math]\displaystyle{ f(t+2)-f(t+1)-f(t)=0 }[/math]

으로 나타낼 수 있다. 이때,

[math]\displaystyle{ \begin{align} \mathcal{L}(f(t+2))&=\int_0^{\infty}e^{-st}f(t+2)dt\\ &=\int_2^{\infty}e^{-s(u-2)}f(u)du\\ &=\int_0^{\infty}e^{-s(u-2)}f(u)du-\int_0^2e^{-s(u-2)}f(u)du\\ &=e^{2s}\mathcal{L}(f(t))-e^{2s}\left(\frac{e^{-s}-e^{-2s}}{s}\right)\\ &=e^{2s}\mathcal{L}(f(t))-\frac{e^s-1}{s} \end{align} }[/math]

이고

[math]\displaystyle{ \mathcal{L}(f(t+1))=e^s \mathcal{L}(f(t)) }[/math]

이다. 그러므로

[math]\displaystyle{ \begin{align} \mathcal{L}(f(t))&=\frac{e^s-1}{s(e^{2s}-e^s-1)}\\ &=\frac{e^s-1}{\sqrt{5}s}\left(\frac{1}{e^s-\frac{1+\sqrt{5}}{2}}-\frac{1}{e^s-\frac{1-\sqrt{5}}{2}}\right)\\ &=\frac{1}{\sqrt{5}}\left(\frac{1-e^{-s}}{s(1-\frac{1+\sqrt{5}}{2}e^{-s})}-\frac{1-e^{-s}}{s(1-\frac{1-\sqrt{5}}{2}e^{-s})}\right)\\ &=\frac{1}{\sqrt{5}}\left(\mathcal{L}\left(\left(\frac{1+\sqrt{5}}{2}\right)^{\lfloor t \rfloor}\right)-\mathcal{L}\left(\left(\frac{1-\sqrt{5}}{2}\right)^{\lfloor t \rfloor}\right)\right) \end{align} }[/math]

이므로 [math]\displaystyle{ \bigcup_{m\in\mathbb{N}}(m,m+1) }[/math]에서

[math]\displaystyle{ f(t)=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^{\lfloor t \rfloor}-\left(\frac{1-\sqrt{5}}{2}\right)^{\lfloor t \rfloor}\right) }[/math]

이고, [math]\displaystyle{ t=n+\frac{1}{2} }[/math]을 대입하면

[math]\displaystyle{ a_n=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right) }[/math]

을 얻는다.나는 괄호가 싫어요

같이 보기

• 푸리에 변환