동적 계획법

Dynamic Programming, 動的計劃法.

개요

수학과 컴퓨터 공학, 경제학에서 쓰이는 동적 계획법은 어떤 복잡한 최적화 문제를, 간단한 작은 부분 문제로 나누어 해결하는 방법을 말한다.

이름이 Dynamic Programming이지만 그닥 역동적인 알고리즘은 아닌데, 예산을 따오기 위해 멋진 이름을 지었다고 카더라(...). 또한 Programming은 컴퓨터 프로그래밍을 의미하는 것이 아니고, 선형계획법처럼 최적화 문제의 해결 방법이라는 의미이다.

컴퓨터 공학에서 Dynamic Programming은 중요한 위치를 차지한다. 시간 복잡도를 낮춤으로써 더 빠르게 문제를 해결하는 해를 얻을 수 있다. 예를 들어, [math]\displaystyle{ O(n^3) }[/math]을 사용해 해결한 문제에 동적 프로그래밍으로 접근이 가능하다면, [math]\displaystyle{ O(n) }[/math]만에 푸는 것도 가능하다. ACM-ICPC 따위의 대회에 많이 출제되는 유형이기도 하며, Baekjoon Online Judge의 알고리즘 분류 기준에서 가장 많은 문제들이 출제되어 있는 알고리즘이다.

설명

주어진 문제를 풀기 위하여 그 문제를 작은 문제들로 나누어 푼 다음, 그 결과들을 조합하여 궁극적 결론에 도달하는 것이다. 이 과정에서 같은 문제를 풀어야 할 경우 메모이제이션 기법을 사용하여 시간을 절약할 수 있다.

예시

그냥 이론을 설명하기에는 복잡하니, 예시를 보며 이해해 보자.

피보나치 수열 구하기

피보나치 수열은 제 0항을 0, 제 1항을 1로 하고, 그 다음 항부터는 이전 두 개 항의 합으로 나타나는 수열이다.

이를 점화식으로 표현하면 [math]\displaystyle{ \mathrm{fib}(n) = \mathrm{fib}(n - 1) + \mathrm{fib}(n - 2) (n \gt 2), \mathrm{fib}(0) = 0, \mathrm{fib}(1) = 1 }[/math]가 된다.

이를 계산하는 프로그램을 작성해 보자. 점화식에 충실하게 재귀함수로 풀면 다음과 같을 것이다. 편의상 Python3으로 작성하였다.

def fib(n):
    if n == 1 or n == 0:
        return n
    return fib(n - 1) + fib(n - 2)

분명 잘 작동하긴 하는데, 문제는 숫자가 조금만 커져도 시간이 너무 오래 걸린다는 점이다. [math]\displaystyle{ \mathrm{fib}(5) }[/math]의 계산 과정을 그림으로 그려보면 다음과 같다.

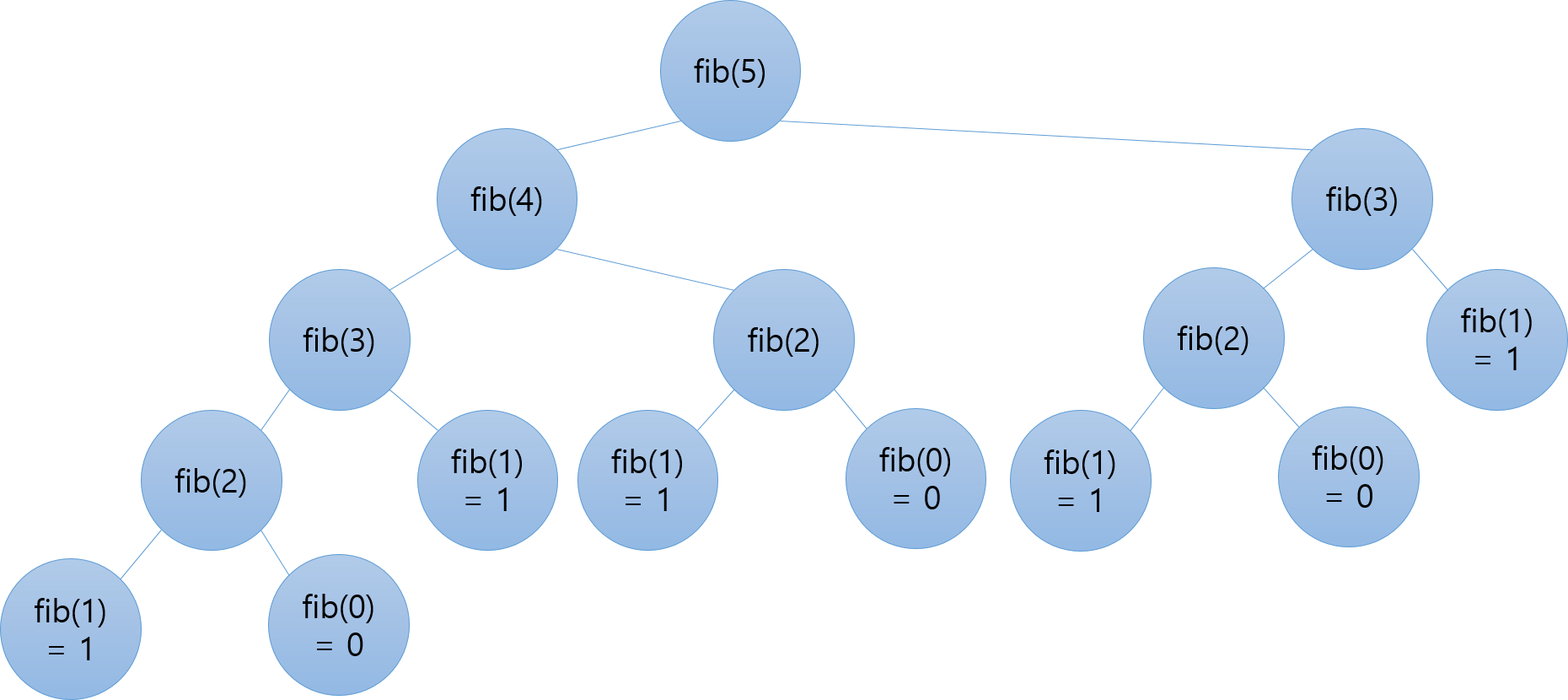
위의 동그라미는 아래 두 개의 동그라미의 합으로 채워진다. 얼마나 많은 계산이 필요한지 알 수 있다. 그런데 저 계산들 중 중복되는 것이 보이지 않는가?

저 과정에서 [math]\displaystyle{ \mathrm{fib}(2) }[/math]는 3번, [math]\displaystyle{ \mathrm{fib}(3) }[/math]는 2번 계산됨을 알 수 있다. 이걸 일일히 계산하지 말고, 한번 구한 값을 그냥 어디 적어(memo)놨다가 다시 쓰면 어떨까?

이 기법이 바로 메모이제이션(memoization)이다.

저 그림의 맨 왼쪽 아래부터 계산하기 시작해보자. [math]\displaystyle{ \mathrm{fib}(2) = 1 + 0 = 1 }[/math]로 채워진다. 그 위의 [math]\displaystyle{ \mathrm{fib}(3) = 1 + 1 = 2 }[/math]가 될 것이다. 이제 [math]\displaystyle{ \mathrm{fib}(4) }[/math]를 계산해야 한다. 원래는 [math]\displaystyle{ \mathrm{fib}(4) = 2 + \mathrm{fib}(2) }[/math]로 오른쪽의 [math]\displaystyle{ \mathrm{fib}(2) }[/math]를 다시 계산해야겠지만, 앞서 [math]\displaystyle{ \mathrm{fib}(2) }[/math]를 계산할 때 어디 적어뒀다면 이를 바로 읽어와 [math]\displaystyle{ \mathrm{fib}(4) = 2 + 1 = 3 }[/math]을 간단히 계산할 수 있다. 마찬가지로, [math]\displaystyle{ \mathrm{fib}(5) }[/math]의 계산 역시 [math]\displaystyle{ \mathrm{fib}(3) }[/math]의 계산 결과가 저장되어 있다면, 곧바로 [math]\displaystyle{ \mathrm{fib}(5) = 3 + 2 = 5 }[/math]라는 값을 구할 수 있다. 메모하지 않았다면 [math]\displaystyle{ \mathrm{fib}(3), \mathrm{fib}(2) }[/math] 따위를 여러번 다시 구해야 할 판인데, 계산이 확 줄어들었다.

코드로 적으면 다음과 같다.

def fib(n):
    DT = [None] * (n + 1)
    DT[0], DT[1] = 0, 1
    return cal_fib(DT, n)

def cal_fib(DT, n):
    if DT[n] == None:
        DT[n] = cal_fib(DT, n - 1) + cal_fib(DT, n - 2)
    return DT[n]

시간 복잡도 분석

우선 메모이제이션을 적용하지 않고 계산했을 때의 시간 복잡도를 구해보자. [math]\displaystyle{ \mathrm{fib}(n) }[/math]을 계산하기 위해서는, [math]\displaystyle{ \mathrm{fib}(n - 1) }[/math]과 [math]\displaystyle{ \mathrm{fib}(n - 2) }[/math]를 계산해야 한다. 계산 시간을 [math]\displaystyle{ T(n) }[/math] 이라고 하면, [math]\displaystyle{ T(n) = T(n - 1) + T(n - 2) }[/math] 이다. 이는 피보나치 수열의 점화식과 같다. big-O 표기법에 따라 쓰면 [math]\displaystyle{ O(\mathrm{fib}(n)) }[/math]이고, 좀 큰 [math]\displaystyle{ n }[/math] 에 대해 [math]\displaystyle{ \mathrm{fib}(n) \approx 1.6^n }[/math] 이므로, [math]\displaystyle{ O(1.6^n) }[/math]로 쓸 수 있다.

지수함수라는 놈이 얼마나 흉악한 놈인지는 다들 알겠지만 한번 짚어보자. [math]\displaystyle{ n = 100 }[/math]정도만 생각해봐도 대충 [math]\displaystyle{ 1.6^{100} = 2.6 \times 10^{20} }[/math]쯤 되는데, 이건 컴퓨터가 뚝딱 계산할 수 있는 양이 아니다. 요즘 CPU 클럭수가 대략 4GHz, 초당 [math]\displaystyle{ 4 \times 10^9 }[/math]회니까, 65,000,000,000초, 752314일쯤 걸리지 않을까? 물론 시간복잡도에 숫자 때려넣은 걸 클럭수로 나눈 것과 실제 수행 시간이 일치하지는 않지만, 대충 감은 잡을 수 있다.

그렇다면 메모이제이션을 적용했을 때는 시간이 얼마나 걸릴까? 이미 계산한 값은 다시 계산하지 않기 때문에, n이 1 증가했을 때 추가되는 시간은 앞서 계산한 [math]\displaystyle{ \mathrm{fib}(n - 1) }[/math]과 [math]\displaystyle{ \mathrm{fib}(n - 2) }[/math]의 합을 구하는 시간만 필요하다. 이는 상수 시간에 해결될 수 있으므로, [math]\displaystyle{ T(n) = T(n - 1) + c }[/math] 이고, 결국 [math]\displaystyle{ T(n) = O(n) }[/math]이다. 지수 시간이 걸리는 문제를, 동적 계획법을 이용해 다항시간에 해결할 수 있음을 알 수 있다.

Bottom-up Approach

메모이제이션을 통해 빠르게 피보나치 수열의 값을 구할 수 있게 되었다. 그런데 문제가 하나 남았다. 저 구현이 아직 재귀함수의 형태를 띠고 있다는 것이다. 재귀함수는 디버깅이 어렵고, 무엇보다 호출 스택의 한계 때문에 일정 이상으로 재귀하게 되면 프로그램이 터져 버리는 문제가 발생할 가능성이 있다. 모든 재귀함수는 반복문으로 고칠 수 있다는 사실이 증명되어 있으므로, 저걸 반복문으로 고치는게 좋겠다.

메모이제이션 재귀에서는 [math]\displaystyle{ \mathrm{fib}(5) }[/math]를 먼저 호출하고, 그 곳에서 [math]\displaystyle{ \mathrm{fib}(4), \mathrm{fib}(3), \cdots }[/math]등을 위에서 아래로 (Top-down) 호출하게 된다. 하지만 실제로 피보나치 수를 저장한 테이블이 차오르는 순서는 반대로, 아래에서부터 올라오게 된다. 위에서 아래로 내려가는 과정을 생략하고, 그냥 아래서부터 채워 올라오는 것이 바로 Bottom-up Approach이다.

def fib(n):
    if n == 0: return 0
    DT = [None] * (n + 1)
    DT[0], DT[1] = 0, 1
    for i in range(2, n + 1): #i = 2부터 n까지 증가한다.
        DT[i] = DT[i - 1] + DT[i - 2]
    return DT[n]

물론 피보나치 수열 문제는 가까운 두 값만 필요하므로, 굳이 리스트(테이블)을 생성하지 않고,

def fib(n):
    if n == 0: return 0
    temp0, temp1 = 0, 1
    for i in range(2, n + 1): #i = 2부터 n까지 증가한다.
        #temp0에는 temp1을, temp1에는 temp0과 temp1을 더한 값을 넣는다.
        temp0, temp1 = temp1, temp0 + temp1
    return temp1

처럼 하면 메모리 공간을 절약할 수 있다. 다만 이 풀이는 동적 계획법 풀이라고 보기는 힘들고, 피보나치 수열을 구하는 수많은 방법 중 하나라고 생각하자. 동적 계획법은 메모리를 희생해서 수행 시간을 개선하는 방법이라고 생각해도 좋다.

거스름돈 문제

리브레 제국의 화폐 체계는 영 이상해서, 이 나라의 상인들은 거스름돈 계산을 힘들어 한다. 국왕인 당신은 이러한 백성들을 어엿비 녀겨 거스름돈을 계산하는 프로그램을 만들기로 결심했다.

이 나라에는 [math]\displaystyle{ x_1 }[/math]원, [math]\displaystyle{ x_2 }[/math]원, [math]\displaystyle{ \cdots , x_i }[/math]원 짜리 동전이 있고, 거슬러 주는 동전의 개수는 최대한 줄여야 한다.

행렬을 곱하는 순서

행렬을 곱할 때, 어떤 것을 먼저 곱하는지에 따라 계산량은 크게 달라진다. 계산을 가능한 한 적게 할 수 있도록, 적절히 괄호를 묶어주기 위한 알고리즘을 생각해보자.