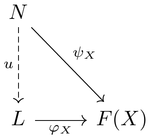극한

다른 뜻에 관한 내용은 극한 (동음이의) 문서를 읽어 주세요.

極限. Limit

개요

사전적 의미는 궁극의 한계. 수학에서의 의미에 대입해보면, 무언가가 궁극적으로 다가가는 값을 말한다고 생각할 수 있다. 극한은 미적분학과 해석학의 시작에 해당하는 매우 중요한 개념이고, 이 직관적인 의미 자체는 고대에도 알려져 있었다.

역사

아르키메데스의 원의 넓이를 구하는 방법이나, 제논의 역설 등을 보면 고대 그리스 시대부터 무한이라는 개념은 존재했다는 사실을 알 수 있다. 물론 그 당시에는 이를 수학적으로 엄밀하게 정의할 생각은 하지 않았다. 시간이 흘러 뉴턴이 이 무한이라는 개념을 사용한 극한이라는 개념을 생각하고, 극한을 사용해 미적분학의 기초를 만든다. 뉴턴을 비롯한 다른 학자들은 극한값을 구하는 것에만 치중하였지, 극한에 대한 엄밀한 성질은 생각하지 않았다. 그래서인지 [math]\displaystyle{ \lim }[/math]와 [math]\displaystyle{ \int }[/math]를 교환을 하는 등, 현대의 수학에서는 (일반적으로) 틀린 성질들을 사용하였다. 수학자들이 물리학자들을 까는 이유 푸리에는 푸리에 급수의 균등수렴성을 증명하지 못하였지만 그대로 식을 사용하였고, 칸토어는 이를 연구하다가 소박한 집합론을 만들었다. ...? 이후에 모든 점에서 불연속인 디리클레 함수, 모든 점에서 연속이지만 모든 점에서 미분이 불가능한 바이어슈트라우스 함수 등의 극한의 직관적인 이해만으로는 제대로 설명할 수 없는 문제점들이 발견되었고, 이에 따라 수학적으로 엄밀한 극한의 정의가 필요하게 되었다. 엄밀한 극한의 정의는 볼차노에 의해 기초가 다져진 뒤, 코시와 바이어슈트라스에 의해 완성되었다. 이 정의가 바로 그 유명한 [math]\displaystyle{ \varepsilon\text{-}\delta }[/math] 논법.

수열의 극한

이와 관련한 내용은 수열의 극한에서 볼 수 있습니다.

수열의 극한은 엡실론-델타와는 살짝 다른 [math]\displaystyle{ \varepsilon\text{-}N }[/math] 논법을 사용한다. 물론 기본적인 골자는 같다.

함수의 극한

이와 관련한 내용은 함수의 극한에서 볼 수 있습니다.

직관적으로, 함수의 변동폭이 매우 작아져 어느 한 점으로 가까이 갈 때, 그 목적지를 극한(값)이라고 한다. 엡실론-델타 논법이나, 근방과 위상 개념으로 정의된다. 극한의 유일성은 하우스도르프 공간에서 보장된다.

적절한 조건 하에서 함수의 극한을 수열의 극한으로 바꿀 수 있어, 계산을 편하게 할 수 있다. 예를 들어, [math]\displaystyle{ \displaystyle \lim_{x \to 0} x }[/math]를 구할 때0이잖아 수렴성이 가정된다면 [math]\displaystyle{ \displaystyle x = \frac{1}{n} \quad (n \in \mathbb N) }[/math]으로 바꾸어 [math]\displaystyle{ \displaystyle \lim_{x \to 0} x = \lim_{n \to \infty} \frac{1}{n} = 0 }[/math] 등으로 구할 수 있다는 것이다.

범주론적인 극한

이와 관련한 내용은 극한 (범주론)에서 볼 수 있습니다.

범주론에서, 극한은 (category의 object들의) 곱, 당김(pullback), 역극한(inverse limit) 등의 공통적인 보편 성질(universal property)을 말하기 위해 만들어진 개념이다. 물론, 범주론적 극한은 위의 모든 극한을 모두 포함한다. 즉, 위상적인 극한은 범주론적 극한의 특수한 경우이다.

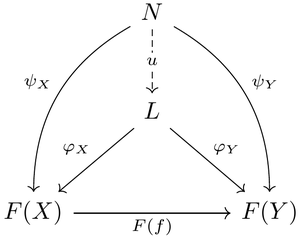
극한의 정의는 universal cone, 즉 보편 성질을 만족하는 뿔이다. 풀어 설명하면 주어진 다이어그램 [math]\displaystyle{ F:\; J \to \mathcal C }[/math]의 극한은, 임의의 뿔(non-universal cone) [math]\displaystyle{ (N, \psi) }[/math]와 어떤 뿔(universal cone) [math]\displaystyle{ (L, \varphi) }[/math]에 대하여 둘의 object 사이에 [math]\displaystyle{ N, L, F(X) }[/math] (F(X)는 주어진 다이어그램의 object)로 이루어진 아래 다이어그램을 가환하게 하는 사상 [math]\displaystyle{ u: \; N \to L }[/math](factorization)이 유일하면(∃!u∀F(X)):

그때의 뿔 [math]\displaystyle{ (L, \varphi) }[/math]를 다이어그램(covariant functor) [math]\displaystyle{ F }[/math]의 극한이라고 한다. 즉, 다음을 가환하게 하는 [math]\displaystyle{ L }[/math]이다.

기존의 극한 개념으로 봤을 때 참으로 뜬금없는 정의인데, 이것이 어떻게 위상적인 극한과 연결되는지를 알고 싶으면 문서 참조.

관련 항목

• 수열의 극한
• 함수의 극한
• 해석학