공종도

[math]\displaystyle{ \omega }[/math]와 그의 한 공종 집합을 나타낸 그림. 선 하나는 [math]\displaystyle{ \le }[/math] 관계를 나타낸다. 이에서 볼 수 있듯이, [math]\displaystyle{ \omega }[/math], 또는 임의의 가산 집합의 공종 집합은 그 기수가 [math]\displaystyle{ \aleph_0 }[/math]여야 한다. 또한, '공종'이라는 용어의 의미 역시 알 수 있다, 즉 '같이 끝나는' 집합을 공종 집합이라고 하는 것이다.

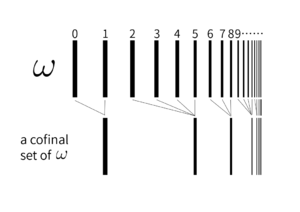
수학에서, 특히 집합론이나 순서론에서, 반순서집합(poset) [math]\displaystyle{ \alpha }[/math]의 공종도(共終度, 영어: cofinality, 일본어: 共終数, 중국어: 共尾性) [math]\displaystyle{ \operatorname{cf}(\alpha) }[/math]는 [math]\displaystyle{ \alpha }[/math]의 공종 부분집합의 최소(least) 기수를 말한다. 이는 서수나 기수가 얼마나 복잡한지를 나타내며, 모든 서수나 기수는 그 공종도에 적절한 연산을 하여 나타낼 수 있다.

또한 공종도를 정의할 때, 기수들의 공 아닌 집합(collection)은 최소원소를 갖는다(well-ordered)는 가정을 하는데, 이는 정렬정리로 선택공리와 동치인 명제이다. 즉, 공종도가 잘 정의되려면 선택공리가 필요하다.

정의

[math]\displaystyle{ A }[/math]를 이항 연산 [math]\displaystyle{ \le }[/math]를 가지고 있는 반순서집합이라고 하자. 만약 다음을 만족하는 [math]\displaystyle{ A }[/math]의 부분집합 [math]\displaystyle{ B\subseteq A }[/math]가 존재하면 [math]\displaystyle{ B }[/math]는 공종 집합(cofinal set)이라고 한다:

모든 [math]\displaystyle{ a \in A }[/math]에 대하여 [math]\displaystyle{ a\le b }[/math]인 [math]\displaystyle{ b\in B }[/math]가 존재한다.

이런 [math]\displaystyle{ B }[/math]의 기수들을 모아 놓은 집합 [math]\displaystyle{ \mathcal B =\{ |B| \} }[/math]의 최소원 [math]\displaystyle{ \lambda }[/math]를 [math]\displaystyle{ A }[/math]의 공종도라고 한다.

서수의 경우

서수, 특히 극한서수(limit ordinal)의 경우, 동치인 정의가 있다:

• [math]\displaystyle{ \alpha }[/math]를 극한서수라 하자. 이때 [math]\displaystyle{ \sup_{i\lt \lambda} \alpha_i = \alpha }[/math]인 [math]\displaystyle{ \langle \alpha_i \lt \alpha: \, i \lt \lambda \rangle }[/math]이 존재하는 [math]\displaystyle{ \lambda }[/math] 중 최소의 것을 [math]\displaystyle{ \alpha }[/math]의 공종도라 한다.
• 서수 [math]\displaystyle{ \alpha }[/math]의 공종도는 그 공종 집합들의 순서형(order type)들 중 가장 작은 서수이다.

정칙 서수와 특이 서수

[math]\displaystyle{ \operatorname{cf}(\alpha) = \alpha }[/math]인 [math]\displaystyle{ \alpha }[/math]를 정칙 서수(regular ordinal)라고 하고, 그렇지 않은 서수를 특이 서수(singular ordinal)이라고 한다. 당연하게도 모든 정칙 서수는 기수이다.

서수 [math]\displaystyle{ \alpha }[/math]에 대하여 다음이 성립한다:

• [math]\displaystyle{ \operatorname{cf}(\alpha) = 0 \Longleftrightarrow \alpha = 0, }[/math]
• [math]\displaystyle{ \operatorname{cf}(\alpha) = 1 \Longleftrightarrow \alpha \mbox{ is a successor ordinal}, }[/math]
• [math]\displaystyle{ \operatorname{cf}(\alpha) = \omega \Longleftarrow \alpha \mbox{ is countable}, }[/math]
• [math]\displaystyle{ \alpha }[/math]가 비가산일 때에는 그 공종도가 [math]\displaystyle{ \omega }[/math]일 수도 있고 더 클 수도 있다.

기수의 경우

위의 일반적인 정의를 cardinal일 때로 국한하여 다시 서술하면

[math]\displaystyle{ \mathrm{cf}(\kappa) = \min \left\{|I| \, \bigg|\, \kappa = \sum_{i \in I} \lambda_i \wedge \forall i \in I(\lambda_i \lt \kappa)\right\} }[/math]

이다. 정의에서 [math]\displaystyle{ \operatorname{cf}(\kappa) \lt \kappa }[/math]인 것은 자명하고([math]\displaystyle{ \kappa = \bigcup_{i\in\kappa} \{i\} }[/math]이므로), 쾨니그 정리에 의하면 [math]\displaystyle{ \kappa\lt \kappa^{\operatorname{cf}(\kappa)} }[/math]이고 [math]\displaystyle{ \kappa\lt \operatorname{cf}(2^\kappa) }[/math]이다.

정칙 기수(regular cardinal) 역시 서수와 마찬가지로 [math]\displaystyle{ \operatorname{cf}(\kappa) = \kappa }[/math]인 [math]\displaystyle{ \kappa }[/math]로 정의되며, 모든 기수 [math]\displaystyle{ \kappa }[/math]에 대하여 [math]\displaystyle{ \operatorname{cf}(\operatorname{cf}(\kappa)) = \operatorname{cf}(\kappa) }[/math]이다 ― 즉 [math]\displaystyle{ \operatorname{cf}(\kappa) }[/math]는 정칙 기수이다.

예시

• 극한서수 [math]\displaystyle{ \alpha }[/math]에 대하여 [math]\displaystyle{ \aleph_\alpha=\sum_{\beta\lt \alpha}\aleph_\beta }[/math]이므로 [math]\displaystyle{ \operatorname{cf}(\aleph_\alpha)=\operatorname{cf}(\alpha) }[/math]이다.
• 모든 정칙 서수는 알레프 수이다. 물론 AC를 가정하였을 때엔 모든 기수가 알레프 수이므로 의미가 없다.
• 쾨니그 정리에 의하면 [math]\displaystyle{ \aleph_0 \lt \operatorname{cf}(2^{\aleph_0}) }[/math]이다. 또한 [math]\displaystyle{ 2^{\aleph_0} = \aleph_1 }[/math](CH), ..., [math]\displaystyle{ 2^{\aleph_0} = \aleph_n \quad (n \lt \omega) }[/math] 등은 모두 ZF(C)와 독립이지만, 반면에 [math]\displaystyle{ \aleph_\omega = \bigcup_{n \lt \omega} \aleph_n }[/math]이고 cofinality의 정의에 의하여 [math]\displaystyle{ \operatorname{cf}(\aleph_\omega) = |\omega|=\aleph_0 }[/math]이다. 그런데, 쾨니그 정리에 의해, [math]\displaystyle{ \aleph_0 \lt \operatorname{cf}(2^{\aleph_0}) }[/math]이므로, 만약 [math]\displaystyle{ 2^{\aleph_0} = \aleph_\omega }[/math]라면 [math]\displaystyle{ \aleph_0 \lt \operatorname{cf}(\aleph_\omega)=\aleph_0 }[/math]이므로 모순이다. 즉, ZF에서, [math]\displaystyle{ 2^{\aleph_0} \neq\aleph_\omega }[/math]이다.

참고문헌

• Kunen, Kenneth (1980). Set Theory: An Introduction to Independence Proofs. Elsevier. ISBN 0-444-86839-9.
• Hrbacek, Karel; Jech, Thomas (1999). Introduction to Set Theory (3 ed.). ISBN 0-8247-7915-0.
• Spencer Unger. Forcing Summer School Lecture Notes. http://homepages.math.uic.edu/~shac/forcing/forcing2014.pdf 에서 2016. 01. 19.에 확인함.