거리공간

정의[편집 | 원본 편집]

[math]\displaystyle{ X }[/math]를 집합이라 하고 [math]\displaystyle{ d }[/math]를 [math]\displaystyle{ X\times X }[/math]로부터 0 이상의 실수의 집합 [math]\displaystyle{ \mathbb{R}^+ }[/math]로의 함수라고 하자. 임의의 [math]\displaystyle{ x,y,z\in X }[/math]에 대해 다음 조건

(1) [math]\displaystyle{ d(x,y)=0 \Leftrightarrow x=y }[/math]

(2) [math]\displaystyle{ d(x,y)=d(y,x) }[/math]

(3) [math]\displaystyle{ d(x,z)\le d(x,y)+d(y,z) }[/math] (삼각부등식)

을 만족하면 [math]\displaystyle{ d:X\times X\to \mathbb{R}^+ }[/math]를 X 위의 거리(metric), 또는 거리함수(distance function)라고 한다. 그리고 [math]\displaystyle{ d(x,y) }[/math]를 x에서 y까지의 거리(distance)라고 한다.~~뭐여 함수도 거리라며~~ 거리함수 d가 주어진 집합 X는 거리공간(metric space)이라고 하고 [math]\displaystyle{ (X,d) }[/math]라고 표기한다.

참고로 영어 단어 metric과 distance는 모두 "거리"라고 번역되는데, 엄밀하게 따지면 distance는 거리 값을 나타내는 스칼라, metric은 미분기하학적 측면에선 텐서이다.

예시[편집 | 원본 편집]

[math]\displaystyle{ \mathbb{R}^n }[/math]에서 [math]\displaystyle{ \mathbf{x}=(x_1,x_2,\cdots, x_n),\mathbf{y}=(y_1,y_2,\cdots,y_n) }[/math]라 하면 [math]\displaystyle{ (\mathbb{R}^n,d_2),(\mathbb{R}^n,d_1),(\mathbb{R}^n,d_\infty) }[/math]는 거리공간이다. 이때
- [math]\displaystyle{ d_2(\mathbf{x},\mathbf{y})=\sqrt{\sum_{i=1}^n (x_i-y_i)^2} }[/math]
- [math]\displaystyle{ d_1(\mathbf{x},\mathbf{y})=\sum_{i=1}^n|x_i-y_i| }[/math]
- [math]\displaystyle{ d_\infty(\mathbf{x},\mathbf{y})=\max\{|x_i-y_i|: i=1,2,\cdots, n\} }[/math]
임의의 집합 [math]\displaystyle{ X }[/math]의 원소 [math]\displaystyle{ x,y }[/math]에 대해 [math]\displaystyle{ d(x,y)=\begin{cases} 1, &x\ne y\\ 0, &x=y \end{cases} }[/math]로 정의하자. 그러면 [math]\displaystyle{ (X,d) }[/math]는 거리공간이다.
[math]\displaystyle{ \mathcal{C}[a,b] }[/math]를 [math]\displaystyle{ [a,b] }[/math]에서 연속인 실함수라고 하자. 그러면 다음 함수 [math]\displaystyle{ d,d' }[/math]는 [math]\displaystyle{ \mathcal{C}[a,b] }[/math]의 거리함수이다.
- [math]\displaystyle{ d(f,g)=\int_a^b |f(x)-g(x)|dx }[/math]
- [math]\displaystyle{ d'(f,g)=\inf\{|f(x)-g(x)|:x\in [a,b]\} }[/math]

점과 집합 사이의 거리[편집 | 원본 편집]

[math]\displaystyle{ (X,d) }[/math]를 거리공간이라 하고, [math]\displaystyle{ A }[/math]는 [math]\displaystyle{ X }[/math]의 공집합이 아닌 부분집합이며, [math]\displaystyle{ x }[/math]는 [math]\displaystyle{ X }[/math]의 원소라고 하자. [math]\displaystyle{ x }[/math]에서 [math]\displaystyle{ A }[/math]까지의 거리 [math]\displaystyle{ d(x,A) }[/math]는

[math]\displaystyle{ d(x,A)=\sup\{d(x,y): y\in A\} }[/math]

로 정의한다.

지름[편집 | 원본 편집]

이와 관련한 내용은 지름에서 볼 수 있습니다.

[math]\displaystyle{ (X,d) }[/math]가 거리공간이고 [math]\displaystyle{ A }[/math]를 [math]\displaystyle{ X }[/math]의 공집합이 아닌 부분집합이라고 하자. 만약 [math]\displaystyle{ \{d(x,y):x,y\in A\} }[/math]가 상계를 가지면 [math]\displaystyle{ A }[/math]를 유계집합(bounded set)이라고 하며

[math]\displaystyle{ \sup\{d(x,y):x,y\in A\} }[/math]

를 [math]\displaystyle{ A }[/math]의 지름(diameter)이라고 한다. 공집합의 지름은 0으로 정의한다. 만약 [math]\displaystyle{ X }[/math]가 유계이면, [math]\displaystyle{ (X,d) }[/math]를 유계거리공간이라고 한다.

열린 집합과 닫힌 집합[편집 | 원본 편집]

거리공간 [math]\displaystyle{ X,d }[/math]에서 [math]\displaystyle{ a\in X }[/math], [math]\displaystyle{ r \gt 0 }[/math]이 주어졌다고 하자. 다음 집합

[math]\displaystyle{ B_d(a, r)=\{ x\in X : d(x,a)\lt r\} }[/math]

을 중심이 [math]\displaystyle{ a }[/math]이고 반지름이 [math]\displaystyle{ r }[/math]인 열린 공(open ball)이라고 한다. 그리고 집합

[math]\displaystyle{ B_d[a, r]=\{ x\in X : d(x,a)\le r\} }[/math]

을 중심이 [math]\displaystyle{ a }[/math]이고 반지름이 [math]\displaystyle{ r }[/math]인 닫힌 공(open ball)이라고 한다. 거리함수를 하나만 다루어 혼동을 일으킬 염려가 없다면 단순히 [math]\displaystyle{ B(a,r), B[a,r] }[/math]로 표기한다.

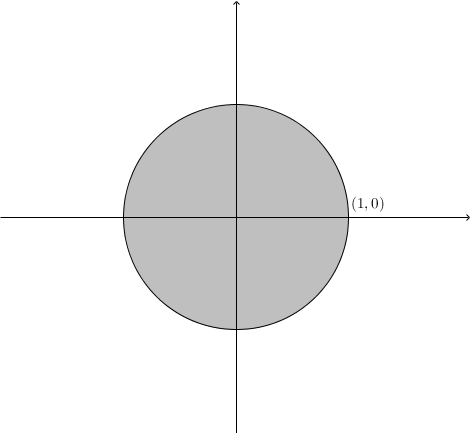
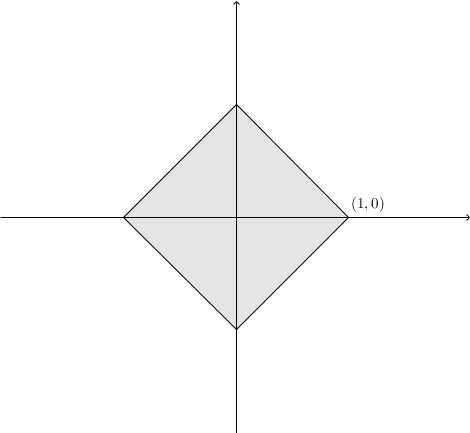
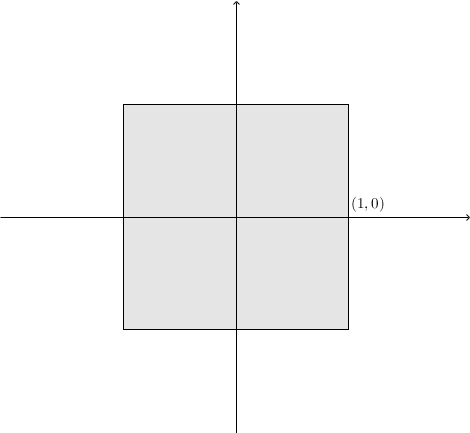
[math]\displaystyle{ (\mathbb{R}^2,d) }[/math]에서 [math]\displaystyle{ d }[/math]의 정의에 따라 공 [math]\displaystyle{ B(\mathbf{0},1) }[/math]의 모습이 달라지는 것을 관찰해보자.

보통거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2} }[/math]	택시거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\|a_1-b_1\|+\|a_2-b_2\| }[/math]

최댓값거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\max\{\|a_1-b_1\|,\|a_2-b_2\|\} }[/math]	이산거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\begin{cases} 0, &\mathbf{a}=\mathbf{b}\\ 1, &\mathbf{a}\ne\mathbf{b} \end{cases} }[/math]

만약 [math]\displaystyle{ (X,d) }[/math]의 부분집합 [math]\displaystyle{ O }[/math]가 열린 공의 합집합으로 주어지면 [math]\displaystyle{ O }[/math]를 거리함수 [math]\displaystyle{ d }[/math]에 대해 열린 집합이라고 한다. 그리고 [math]\displaystyle{ (X,d) }[/math]의 부분집합 [math]\displaystyle{ C }[/math]에 대해 [math]\displaystyle{ X\setminus C }[/math]가 [math]\displaystyle{ d }[/math]에 대해 열린 집합이면 [math]\displaystyle{ C }[/math]를 [math]\displaystyle{ d }[/math]에 대해 닫힌 집합이라고 한다.

거리공간 [math]\displaystyle{ (X,d) }[/math]에서 다음 성질이 성립한다.

[math]\displaystyle{ X }[/math]와 [math]\displaystyle{ \emptyset }[/math]은 열린 집합이다.
열린 집합의 합집합은 열린 집합이다.
유한 개 열린 집합의 교집합은 열린 집합이다.

수열의 극한[편집 | 원본 편집]

이와 관련한 내용은 수열의 극한에서 볼 수 있습니다.

[math]\displaystyle{ (X,d) }[/math]가 거리공간이고 [math]\displaystyle{ (x_n) }[/math]을 X의 점열이라고 하자. 임의의 실수 [math]\displaystyle{ \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ N\in \mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ d \left( x_n , x \right) \lt \varepsilon }[/math]일 때, [math]\displaystyle{ (x_n) }[/math]은 x에 수렴한다고 한다.

거리공간에서 수렴하는 수열의 극한값은 유일하다. [math]\displaystyle{ X }[/math]에서 수렴하는 수열 [math]\displaystyle{ (x_n) }[/math]의 극한값을 [math]\displaystyle{ \alpha,\beta }[/math]라고 하자. 그러면 임의의 [math]\displaystyle{ \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ N_1, N_2 \in \mathbb{N} }[/math]이 존재해 모든 [math]\displaystyle{ n \gt \max\{N_1,N_2\} }[/math]에 대해 [math]\displaystyle{ d (x_n, \alpha) \lt \frac{\varepsilon}{2} }[/math]이고 [math]\displaystyle{ d (x_n,\beta)\lt \frac{\varepsilon}{2} }[/math]이다. 그러면 거리함수의 정의에 의해

[math]\displaystyle{ d(\alpha,\beta) \le d(\alpha, x_n)+d(x_n,\beta) \lt \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon }[/math]

이다. [math]\displaystyle{ \varepsilon }[/math]이 임의의 양수이므로 [math]\displaystyle{ d(\alpha,\beta)=0 }[/math], 즉 [math]\displaystyle{ \alpha=\beta }[/math]임을 안다.

연속함수[편집 | 원본 편집]

이와 관련한 내용은 연속함수에서 볼 수 있습니다.

[math]\displaystyle{ f:(X,d)\to (Y,d') }[/math]를 거리공간 [math]\displaystyle{ (X,d) }[/math]에서 [math]\displaystyle{ (Y,d') }[/math]로의 함수이고, [math]\displaystyle{ a\in X }[/math]라고 하자. 이때 임의의 [math]\displaystyle{ \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \delta \gt 0 }[/math]이 존재해 임의의 [math]\displaystyle{ x\in X }[/math]에 대해 [math]\displaystyle{ d(x,a)\lt \delta }[/math]이면 [math]\displaystyle{ d(f(x),f(a))\lt \varepsilon }[/math]일 때, [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ a }[/math]에서 연속이라고 한다.

동등한 거리공간[편집 | 원본 편집]

거리동형[편집 | 원본 편집]

이와 관련한 내용은 등거리사상에서 볼 수 있습니다.

거리공간 [math]\displaystyle{ (X,d), (Y,d') }[/math]에 대해 일대일 대응 [math]\displaystyle{ f:X\to Y }[/math]가 존재해 임의의 [math]\displaystyle{ a,b\in X }[/math]에 대해

[math]\displaystyle{ d(a,b)=d'(f(a),f(b)) }[/math]

이면 [math]\displaystyle{ (X,d), (Y,d') }[/math]는 거리동형(metrically equivalent) 또는 등거리(isometric)라고 하고, [math]\displaystyle{ f }[/math]는 등거리사상(isometry)이라고 한다.

위상동형[편집 | 원본 편집]

이와 관련한 내용은 위상동형사상에서 볼 수 있습니다.

거리공간 [math]\displaystyle{ (X,d), (Y,d') }[/math]에 대해 일대일 대응 [math]\displaystyle{ f:X\to Y }[/math]가 존재해 [math]\displaystyle{ f }[/math]와 그 역함수 [math]\displaystyle{ f^{-1} }[/math]이 연속이면 [math]\displaystyle{ X,Y }[/math]는 위상적으로 동치(topologically equivalent), 또는 위상동형(homeomorphic)이라고 하고, f는 위상동형사상(homeomorphism)이라고 한다.

완비거리공간[편집 | 원본 편집]

이와 관련한 내용은 완비거리공간에서 볼 수 있습니다.

거리공간 [math]\displaystyle{ (X,d) }[/math]에서 [math]\displaystyle{ X }[/math]의 모든 코시수열이 [math]\displaystyle{ X }[/math]의 점으로 수렴하면 [math]\displaystyle{ (X,d) }[/math]를 완비거리공간(complete metric space)이라고 한다.

부분공간[편집 | 원본 편집]

[math]\displaystyle{ (X,d) }[/math]를 거리공간이라 하고 [math]\displaystyle{ Y }[/math]를 [math]\displaystyle{ X }[/math]의 부분집합이라 하자. [math]\displaystyle{ d':Y\times Y \to \mathbb{R} }[/math]을

[math]\displaystyle{ d'(x,y)=d(x,y)\text{ for all }x,y\in Y }[/math]

로 두면 [math]\displaystyle{ (Y,d') }[/math]는 거리공간이다. 이때 [math]\displaystyle{ (Y,d') }[/math]를 [math]\displaystyle{ (X,d) }[/math]의 부분공간(subspace)이라고 한다.

위상적 성질[편집 | 원본 편집]

거리공간은 다음 위상적 성질을 가진다.

모든 거리공간은 제1가산공간이다.

거리공간 [math]\displaystyle{ (X,d) }[/math]의 임의의 점 [math]\displaystyle{ a }[/math]에서 열린 공의 모임

[math]\displaystyle{ \mathcal{B}_a=\left\{B\left(a,\frac{1}{n}\right): n\in \mathbb{N}\right\} }[/math]

이 가산집합이고 [math]\displaystyle{ a }[/math]가 [math]\displaystyle{ \mathcal{B}_a }[/math]의 임의의 원소의 원소임은 명백하다. 이제 [math]\displaystyle{ a }[/math]를 포함하는 열린 집합 [math]\displaystyle{ O }[/math]를 하나 생각하자. [math]\displaystyle{ O }[/math]가 열린 집합이므로, [math]\displaystyle{ B(a,\varepsilon) }[/math]가 [math]\displaystyle{ O }[/math]의 부분집합이 되도록 하는 [math]\displaystyle{ \varepsilon\gt 0 }[/math]이 존재한다. 그러면 아르키메데스의 원리에 의해 [math]\displaystyle{ n \gt \frac{1}{\varepsilon} }[/math]인 자연수 [math]\displaystyle{ n }[/math]이 존재하고

[math]\displaystyle{ B\left(a,\frac{1}{n}\right) \subseteq B(a,\varepsilon)\subseteq O }[/math]

이다. 따라서 [math]\displaystyle{ \mathcal{B}_a }[/math]가 가산국소기저이므로 원하는 결론을 얻는다.

모든 거리공간은 하우스도르프 공간이다.

거리공간 [math]\displaystyle{ (X,d) }[/math]의 임의의 원소 [math]\displaystyle{ a,b }[/math]에 대해 열린 공 [math]\displaystyle{ B\left(a,\frac{1}{2}d(a,b)\right),B\left(b,\frac{1}{2}d(a,b)\right) }[/math]을 설정하면 두 집합은 각각 [math]\displaystyle{ a,b }[/math]를 포함하고 서로소이다. 따라서 원하는 결론을 얻는다.