미분

微分, Differentiation쌀가루(米粉), 적분 거꾸로

e^x 미분해봐” “x e^(x-1) 이지 ㅡ;”

개요

미분(differentiation)이란 어떤 함수로부터 도함수(derivative)를 얻는 것을 말하고, 미분(differential)은 어떤 함수의 선형 근사 함수를 말한다.

다시 말하면, 어떤 함수를 미분(differentiate)하면 미분(differential)이 나오는 게 아니고 도함수(derivative)가 나온다. 뭔 당연한 소리를 그렇게 강조하냐고 생각할 수 있는데, [math]\displaystyle{ f(x) }[/math]를 미분하면 나오는 게 뭐냐고 했을 때 보통 ‘미분’이라거나 딴소리를 하지 ‘도함수’라고 이름을 제대로 불러 주는 사람은 생각보다 적다. 도함수란 각 점에 대해 그 점에서의 미분계수(differential coefficient)를 대응시키는 함수를 말하고, 미분계수는 대강 말하면 그 점에서의 기울기, 즉 순간변화율이다.

좀 더 자세히 설명하자면, 미분이라는 용어는 서로 다른 두 개념 미분(differentiation)과 미분(differential)으로 동시에 쓰이기 때문에 이를 구분할 필요가 있다. Differentiation은 differentiate의 명사형이고, differentiate는 우리가 흔히 미분이라 부르는 도함수를 얻는 것을 말하는 동사이다. 또한 differential은 고등학교에 나오지 않는 개념으로, 원함수의 선형 근사 함수를 말한다. 가령 일변수 함수 [math]\displaystyle{ f(x) }[/math]의 한 점 [math]\displaystyle{ a }[/math]에서의 미분(differential)은[math]\displaystyle{ \mathrm df = f'(a)\mathrm d x }[/math]로 나타나는 선형함수를 말한다. 좀 더 일반적으로 [math]\displaystyle{ a }[/math] 자체도 변수로 다루면서 [math]\displaystyle{ f(x) }[/math]의 미분 [math]\displaystyle{ \mathrm df }[/math]를[math]\displaystyle{ \mathrm d f(x,{\Delta x})=f'(x){\Delta x} }[/math]의 이변수 함수로서 정의 한다. 이 함수를 무한소(infintesimal)로 취급하기도 하며, 여기서 [math]\displaystyle{ {\Delta x} }[/math]는 단순히 변수의 표기에 불과하니 오해하지 말자.

왜 이러한 differential이라는 개념이 필요한가는 다변수함수의 미분으로 가면 확실해진다. 일변수 함수에서는 변화하는 '방향'을 고려할 필요가 없기 때문에 평균변화율이나 순간변화율이 유일하게 결정되지만 이차원으로만 가도 서로다른 방향으로의 무수히 많은 변화율을 생각할 수 있기 때문에 단순하게 일차원의 변화율(직선의 기울기)을 적용하기에는 애로사항이 존재하게 된다.따라서 미분의 개념에 대해 다른 방향으로 접근해야하고 그것이 바로 선형근사함수이다.(정확히는 방향을 고정하면 이런식의 미분값들을 생각할 수는 있다. 방향도함수라고 하는데 편미분도 여기에 속한다. 하지만 모든 방향에 대해서 방향도함수값은 존재하지만 연속은 안 되는 골때리는 상황도 존재하므로 다른 방향의 일반화를 생각하는 것이다.)

[math]\displaystyle{ \mathbb R^n }[/math]에서 [math]\displaystyle{ \mathbb R^m }[/math]으로 가는 함수 [math]\displaystyle{ f:\mathbb x\mapsto f(\mathbf x) }[/math]에 대해 한 점 [math]\displaystyle{ \mathbf a }[/math]를 고정시키고 이로 만든 새로운 함수 [math]\displaystyle{ f(\mathbf x)-f(\mathbf a) }[/math]와 원점 근방에서 가장 원함수와 비슷한 선형 근사 함수는 유일하게 결정할 수 있게 되고, 이러한 방향으로 생각한 일변수 함수에서의 미분의 확장은 타당하다 할 수 있다. 이때 [math]\displaystyle{ f(\mathbf x) }[/math]의 [math]\displaystyle{ \mathbf x=\mathbf a }[/math]에서의 선형 근사 함수 [math]\displaystyle{ L(\mathbf x)=A\mathbf x }[/math]가 위에서 말한 [math]\displaystyle{ \mathbf a }[/math]에서의 미분(differential)이고 이러한 미분의 계수를 미분계수라고 하게 된다. (따라서 차원이 높아지면 이러한 '계수'는 하나의 수가 아닌 행렬로 나타난다.) 모든 고등학생이 도함수의 값을 미분계수라고 부른다는걸 알고 있지만 정작 왜 미분계수라고 부르는지는 잘 모르는데 말그대로 미분(differential)의 계수(coefficient)이기 때문에 그렇게 부르는 것이다.

이렇게 다변수로 가면 미분(differential)을 먼저 정의해야 그로서 미분계수라는 용어가 자연스럽게 나오고 그 미분계수와 해당하는 점을 이어주는 함수를 도함수(derivative)라고 정의할 수 있게 된다.

역사

미분법은 곡선에 접선을 그리는 문제와 함수의 극댓값, 극솟값을 구하는 문제를 연구하는 데서 비롯되었다는 것이 정설이다. 17세기에 케플러는 함수가 극댓값이나 극솟값을 갖는 점의 근방에서는 함수의 증분이 거의 0에 가깝다는 점을 지적했다.

데카르트와 페르마는 해석기하를 고안하여 곡선의 접선을 구하는 방법, 함수의 극대, 극소를 찾는 방법에 대한 연구를 본격적으로 하기 시작했다. 특히 페르마는 케플러의 아이디어를 극댓값과 극솟값을 결정하는 방법으로 변형했다.

그의 방법은 함수 [math]\displaystyle{ f(x) }[/math]에 대하여 [math]\displaystyle{ \frac{f(x+h)-f(x)}{h} }[/math]를 계산한 다음 [math]\displaystyle{ h=0 }[/math]일 때 이식의 값이 0이 되는 점을 찾는 것과 같다. 페르마의 방법은 완벽하지 못했지만 결국 [math]\displaystyle{ f'(x)=0 }[/math]을 만족시키는 x의 값을 찾는 것이므로 오늘날에는 ‘페르마의 정리’ 혹은 ‘내부 극값 정리(interior extremum theorem)’라고 부른다.

함수 [math]\displaystyle{ f(x) }[/math]가 [math]\displaystyle{ x=a }[/math]에서 극값을 가질 때, 만일 [math]\displaystyle{ f(x) }[/math]가 [math]\displaystyle{ x=a }[/math]에서 미분가능하면 [math]\displaystyle{ f'(a)=0 }[/math]이다.

그러나 페르마의 방법에서 [math]\displaystyle{ f'(a)=0 }[/math]은 함수 [math]\displaystyle{ f(x) }[/math]가 [math]\displaystyle{ x=a }[/math]에서 극값을 가질 충분조건은 아니며, 또한 [math]\displaystyle{ f'(a)=0 }[/math]이고 [math]\displaystyle{ x=a }[/math]에서 극값을 갖는다고 하더라도 그 값이 극댓값인지 극솟값인지를 판단할 수는 없다.

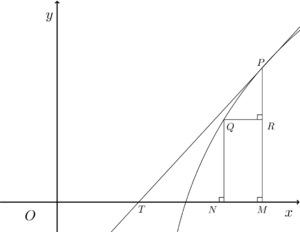
뉴턴 이전에 미분법에 관한 가장 현대적인 접근 방법을 보인 사람은 뉴턴의 스승이고 뉴턴에게 자신의 교수직을 물려준 것으로 유명한 배로이다. 배로는 그의 저서 ‘광학과 기하학 강의’에서 미소 삼각형을 이용한 접선을 찾는 방법을 보였는데, 오른쪽 그림에서 곡선 위의 점 Q가 점 P에 가까워지면 점 P에서 곡선에 그은 접선의 기울기 [math]\displaystyle{ \frac{\overline{PM}}{\overline{TM}} }[/math]은 [math]\displaystyle{ \frac{\overline{PR}}{\overline{QR}} }[/math]에 가까워짐을 이용하여 접선을 구했다.

배로는 자신의 방법으로 많은 곡선들의 접선을 구하는 데 성공했다. 그는 또한 미분법과 적분법이 역연산임을 알아낸 최초의 수학자로 알려져 있는데, 이 중요한 정리가 ‘미적분의 기본 정리’로 ‘광학과 기하학 강의’에 수록되어 있다.

미적분학의 본격적인 정립은 뉴턴과 라이프니츠에 의해 이루어졌다. 뉴턴은 물체의 운동과 그 변화를 나타내기 위한 역학적인 관점에서, 라이프니츠는곡선에 접선을 긋는 기하학적인 관점에서 미분의 아이디어를 생각해 냈다.

뉴턴은 저서 유율법(method of fluxions)에서 곡선을 점의 운동에 의한 자취로 보고 그 좌표의 변화율을 유율이라 하여 미분을 정의하였다. 변하는 양은 변량(fluent)이라하고 그것의 (시간에 대한) 변화율을 유율(fluxion)이라고 한다. 그리고 하나의 변량이 사긴이 0인 무한히 작은 구간에서 증가하는 양을 모멘트(moment)라 정의했다. 곡선을 좌표평면에 나타낼때, 곡선의 좌표 x, y는 변량이고 이것의 유율을 [math]\displaystyle{ \dot{x}, \dot{y} }[/math]로 나타내는데 시간을 [math]\displaystyle{ t }[/math]라고 하면 [math]\displaystyle{ \dot{x}, \dot{y} }[/math]은 각각 [math]\displaystyle{ \frac{\mathrm dx}{\mathrm dt}, \frac{\mathrm dy}{\mathrm dt} }[/math]에 대응된다.

라이프니츠의 미적분학의 강점은 기호 표현에 있다. 라이프니츠는 합을 나타내는 라틴어 Summa의 첫 알파벳 S를 길게 늘인 현대적인 적분 기호 [math]\displaystyle{ \int \cdot \mathrm dx }[/math]와 [math]\displaystyle{ \mathrm dx, \mathrm dy }[/math] 등의 기호를 처음 사용하였다. 현대의 수학 기호와 거의 유사한 라이프니츠의 기호는 뉴턴의 기호에 비해 편리하여, 미적분을 계산 기술로 발전시키는 데 크게 기여했다.

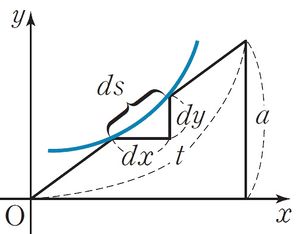
라이프니츠는 곡선의 접선을 긋는 문제와 관련하여 미분의 아이디어를 전개했다. 그림과 같이 주어진 곡선에 접선을 그었다고 하자. [math]\displaystyle{ y }[/math]좌표가 [math]\displaystyle{ a }[/math]일 때, 접선의 길이를 [math]\displaystyle{ t }[/math]라고 하면 삼각형의 닮음에 의하여 다음 관계가 성립한다.

[math]\displaystyle{ \frac{ds}{t}=\frac{dy}{a}, \ ads=tdy }[/math]. 즉 [math]\displaystyle{ \int a \, ds = \int t \, dy }[/math]

이러한 아이디어는 페르마와 배로의 아이디어와도 일맥상통하는 것이다.

뉴턴과 라이프니츠는 각기 다른 방법으로 미분의 아이디어에 도달했음에도 불구하고 이를 둘러싼 뉴턴과 라이프니츠의 우선권 논쟁은 유명하다. 뉴턴과 라이프니츠의 대립은 영국과 유럽 대륙의 싸움으로 번졌다. 오늘날에는 두 사람이 각기 독립적으로 연구했고 미적분학의 발견은 뉴턴이 앞섰지만 발표는 라이프니츠가 먼저이며, 표기법에 있어서는 라이프니츠가 우위인 것으로 인정된다.

17세기 정립된 미적분학의 토대 위에 18세기는 미분과 방정식을 결합시킨 미분방정식을 탐구하게 되었다. 18세기 유명한 수학자들은 자신의 이름이 붙은 미분방정식을 내놓았다. 오일러, 클레로, 달랑베르, 리카티, 르장드르의 미분방정식이 있다. 또한 라플라스는 라플라스 변환으로 미분방정식을 간편하게 해결할 수 있는 방법을 제안하였으며, 18세기 말에는 미분을 기하학에 적용시킨 미분기하학이 등장하여 곡선과 곡면의 성질을 미적분의 관점에서 연구하게 되었다. 19세기 코시는 ε-δ 논법을 이용하여 극한, 연속, 미분가능 등의 개념을 수학적으로 보다 엄밀하게 정의하여 미적분학은 학문적으로 더욱 발전하였다. 이와 같이 미적분학이 발전하는 가운데 예기치 않은 함수들도 발견하게 되었다. 바이어슈트라스는 모든 점에서 미분불가능한 연속함수(바이어슈트라스 함수)를 발견하였고 디리클레 함수가 발견되어 해석학의 기초에 대한 보다 깊이 있는 이해의 필요성이 증대되었다.

미분계수

함수 [math]\displaystyle{ y=f(x) }[/math]에 대하여 [math]\displaystyle{ x }[/math]의 값이 [math]\displaystyle{ a }[/math]에서 [math]\displaystyle{ b }[/math]까지 변할 때, 함숫값은 [math]\displaystyle{ f(a) }[/math]에서 [math]\displaystyle{ f(b) }[/math]까지 변한다. 이때 [math]\displaystyle{ x }[/math]값의 변화량을 [math]\displaystyle{ \Delta x:=b-a }[/math], [math]\displaystyle{ y }[/math]값의 변화량을 [math]\displaystyle{ \Delta y:=f(b)-f(a) }[/math]로 나타낼 때
[math]\displaystyle{ \frac{\Delta y}{\Delta x} = \frac{f(b)-f(a)}{b-a} = \frac{f(a+\Delta x) - f(a)}{\Delta x} }[/math]
를 [math]\displaystyle{ x }[/math]의 값이 [math]\displaystyle{ a }[/math]에서 [math]\displaystyle{ b }[/math]까지 변할 때 [math]\displaystyle{ y=f(x) }[/math]의 평균변화율(average rate of change)이라 한다.
기하학적으로 생각한다면 [math]\displaystyle{ (a,f(a)) }[/math]와 [math]\displaystyle{ (b,f(b)) }[/math]를 잇는 직선의 기울기가 평균변화율이 된다.

여기서 [math]\displaystyle{ \Delta x \to 0 }[/math]일 때, 평균변화율의 극한값
[math]\displaystyle{ \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{f(a+\Delta x) - f(a)}{\Delta x} }[/math]
이 존재하면 [math]\displaystyle{ y=f(x) }[/math]는 [math]\displaystyle{ x=a }[/math]에서 미분가능(differentiable at a)한다. 또한 이 극한값을 [math]\displaystyle{ x=a }[/math]에서의 f의 미분계수(derivative of f at a), 또는 순간변화율(instantaneous rate of change)라 하고 기호로 [math]\displaystyle{ f'(a) }[/math], [math]\displaystyle{ y'(a) }[/math], [math]\displaystyle{ y'|_{x=a} }[/math] 또는 [math]\displaystyle{ \frac{\mathrm df}{\mathrm dx}(a) }[/math]라 표현한다.

도함수

함수 [math]\displaystyle{ f: [a,b] \to \mathbb{R} }[/math]에 대하여 함수 [math]\displaystyle{ f }[/math]가 미분가능한 점 [math]\displaystyle{ x \in [a,b] }[/math]전체의 집합을 E라고 하면 E의 각 점 [math]\displaystyle{ x }[/math]에 대하여 그 점에서의 미분계수[math]\displaystyle{ f'(x) }[/math]를 대응시킬 수 있다. 여기서 함수 [math]\displaystyle{ f }[/math]에 대하여 새로운 함수[math]\displaystyle{ g: E \to \mathbb{R} }[/math]을 [math]\displaystyle{ g(x)=f'(x) }[/math]로 정의할 때, 이 함수 [math]\displaystyle{ g }[/math]를 [math]\displaystyle{ f }[/math]의 도함수(derived function of f, derivative of f)라고 하고 이를 기호로 [math]\displaystyle{ f' }[/math] 또는 [math]\displaystyle{ \frac{\mathrm df}{\mathrm dx} }[/math]로 나타낸다.

상수 [math]\displaystyle{ c\in \mathbb{R} }[/math]와 미분가능한 함수 [math]\displaystyle{ f,g }[/math]의 도함수 [math]\displaystyle{ f',g' }[/math]에 대해 다음 식이 성립한다.

• [math]\displaystyle{ (f+g)'=f'+g' }[/math]

[math]\displaystyle{ \begin{align} (f+g)'(x)&=\lim_{h\to 0}\frac{(f(x+h)+g(x+h))-(f(x)+g(x))}{h}\\ &=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}+\lim_{h\to 0}\frac{g(x+h)-g(x)}{h}\\ &=f'(x)+g'(x) \end{align} }[/math]

• [math]\displaystyle{ (cf)'=cf' }[/math]

[math]\displaystyle{ \begin{align} (cf)'(x)&=\lim_{h\to 0}\frac{cf(x+h)-cf(x)}{h}\\ &=c\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\\ &=cf'(x) \end{align} }[/math]

• [math]\displaystyle{ (fg)'=f'g+fg' }[/math]

[math]\displaystyle{ \begin{align} (fg)'(x)&=\lim_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}\\ &=\lim_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h}\\ &=\lim_{h\to 0}\frac{(f(x+h)-f(x))g(x+h)+f(x)(g(x+h)-g(x))}{h}\\ &=\lim_{h\to 0}\frac{(f(x+h)-f(x)}{h}\lim_{h\to 0}g(x+h) + \lim_{h\to 0}f(x)\lim_{h\to 0}\frac{g(x+h)-g(x)}{h}\\ &=f'(x)g(x)+f(x)g'(x) \end{align} }[/math]

• [math]\displaystyle{ \left(\frac{f}{g}\right)'=\frac{f'g-fg'}{g^2}\;(g(x)\ne 0) }[/math]

[math]\displaystyle{ \left(\frac{1}{g}\right)' }[/math]의 도함수를 먼저 구해보면

[math]\displaystyle{ \begin{align} \left(\frac{1}{g}\right)'(x)&=\lim_{h\to 0}\frac{\frac{1}{g(x+h)}-\frac{1}{g(x)}}{h}\\ &=\lim_{h\to 0}\frac{g(x)-g(x+h)}{hg(x)g(x+h)}\\ &=-\frac{g'(x)}{(g(x))^2} \end{align} }[/math]

이므로

[math]\displaystyle{ \begin{align} \left(\frac{f}{g}\right)'&=\left(f\cdot \frac{1}{g}\right)'\\ &=f'(x)\frac{1}{g}(x)+f(x)\left(\frac{1}{g}\right)'(x)\\ &=\frac{f'(x)}{g(x)}-f(x)\cdot \frac{g'(x)}{(g(x))^2}\\ &=\frac{f'(x)g(x)-f(x)g'(x)}{(g(x))^2} \end{align} }[/math]

이다.

차분

수열[math]\displaystyle{ \{ a_n \} }[/math]에서는 정의역이 조밀하지 못하므로 극한은 구할 수 없다. 대신 [math]\displaystyle{ \Delta a_n = a_{n+1} - a_n }[/math]가 미분과 비슷한 의미를 갖는데 이를 차분(difference)이라 한다.

찰스 배비지가 만들었다는 차분 기관(difference engine)의 차분이 바로 이것이다!

아니 계차수열 아니냐고? [math]\displaystyle{ f'(a) }[/math]가 미분계수이고 [math]\displaystyle{ f'(x) }[/math]가 도함수였듯, [math]\displaystyle{ \Delta a_n }[/math]은 차분이고 [math]\displaystyle{ \{ \Delta a_n \} }[/math]가 계차수열이다.

미분에 관한 공식을 차분에 관해서도 비슷하게 다 말할 수 있다. 예를 들어 합의 차분, 곱의 차분 등을 말할 수 있다. 차분방정식도 있다!

둘러보기

• 적분

참고문헌

• 황선욱 외 10인, 고등학교 미적분 I 교사용 지도서, (주)좋은책신사고, 2015
• 우정호 외, 고등학교 미적분 I 교사용 지도서, 두산동아, 2014
• 정동명·조승제, 실해석학 개론, 경문사, 2004