유체역학(流體力學)은 유체의 운동에 대한 역학이다. 정지되어 있는 유체역학인 유체 정역학(流體靜力學과 유체가 운동하는 유체 동역학(流體動力學)으로 나뉜다. 유체는 약한 응집력과 용기 벽에 작용하는 힘에 의해 결합된 무질서한 분자들의 집합이며, 액체와 기체는 모두 유체이다.
압력[편집 | 원본 편집]
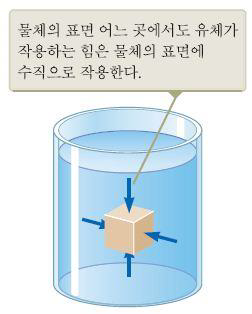
유체가 물체에 가하는 힘은 위쪽 그림과 같이 항상 수직이다.
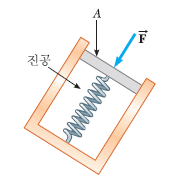
유체 내부의 압력은 위의 그림과 같은 장치로 측정할 수 있다. 피스톤에 작용하는 힘이 F이고 피스톤의 넓이가 A이면, 장치가 잠긴 위치에서 유체의 압력P는 단위 넓이당 힘의 크기로 정의한다.
“ [math]\displaystyle{ P \equiv \frac{F}{A} }[/math] “
만일 압력이 면 위의 위치에 따라 다르다면, 작은 넓이 dA에 작용하는 작은 힘 dF는 다음과 같다.
“ [math]\displaystyle{ dF = PdA }[/math] “
압력의 단위는 SI단위계에서 N/m2이다. 이것의 다른 이름은 파스칼(Pa)이다.
깊이에 따른 압력의 변화[편집 | 원본 편집]
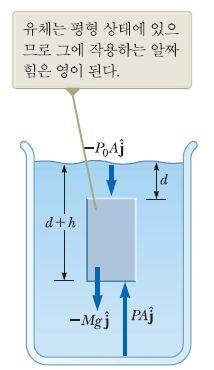
밀도가 ρ인 정지한 액체를 생각해보자. ρ는 유체 내에서 일정한 값이라고 가정하자. 단면의 넓이는 A인 가상의 원통이 깊이 d에서부터 d+h인 곳까지 있고 그속에 들어 있는 액체를 생각해보자. 원통의 밑면에서 액체가 가하는 압력은 P이고 원통의 위에서 액체가 가하는 압력은 P0이다. 따라서 원통의 밑면에서 액체가 작용하는 힘은 PA이고 위에서 작용하는 힘은 P0A이다. 원통속의 액체의 질량은 [math]\displaystyle{ M = \rho V = \rho Ah }[/math]이므로 원통속에 있는 액체의 무게는 [math]\displaystyle{ Mg = \rho Ahg }[/math]이다. 따라서 다음과 같은 식을 얻을수 있다.
[math]\displaystyle{ \sum F = PA - {P}_{0} - Mg = 0 }[/math]
또는
[math]\displaystyle{ PA - {P}_{0}A - \rho Ahg = 0 }[/math]
“ [math]\displaystyle{ P = {P}_{0} + \rho gh }[/math] “
이 식은 용기의 모양에 관계없이 깊이가 같은 모든 지점에서의 압력이 같다는 것을 의미한다.
유체에 의한 압력은 깊이와 P0의 값에 비례하므로, 유체 표면에 압력을 증가시키면 압력은 유체 내부의 각 접에 똑같이 전달된다. 이 사실은 프랑스의 과학자 파스칼이 처음 발견하여 파스칼의 법칙이라 한다.
“ 유체에 작용하는 압력의 변화는 유체 내의 각 점과 용기의 벽에 똑같이 전달된다. “
부력과 아르키메데스의 원리[편집 | 원본 편집]
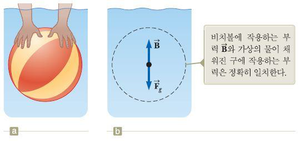
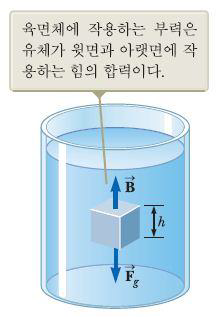
부력은 유체에 잠긴 물체에 작용하여 위로 떠오르는 힘이다. 부력의 크기를 간단하게 결정지을수가 있다. 우선 위의 그림을 보듯이 물 아래에 비치볼 크기의 구가 있다고 생각해보자. 이 구는 평형상태에 있으므로 중력의 힘을 상쇄하는 다른 힘이 필요하다. 이 다른힘이 부력이다. 그리고 부력의 크기는 가상의 구를 채우고 있는 물의 무게와 같다. 이제 이 구를 실제의 비치볼로 생각하자. 비치볼을 둘러싼 유체가 작용하는 알짜힘은 앞의 구의 주변 유체가 작용하는 힘과 같다. 따라서
“ 어떤 물체에 작용하는 부력은 그 물체에 의해 밀려난 유체의 무게와 같다.
아르키메데스의 원리“
부력의 발생원리를 잘 이해하기 위해 오른쪽 그림처럼 유체 속에 잠긴 딱딱한 물체를 생각해보자. [math]\displaystyle{ P = {P}_{0} + \rho gh }[/math]이 식에 따르면 밑면의 압력 Pbot은 윗면에 작용하는 압력 Ptop보다 ρfluidgh만큼 크다. 여기서 ρfluid는 유체의 밀도이고, h는 물체의 높이이다. 물체 밑면의 압력은 위로 향하는 힘을 만드는데 이는 PbotA과 같다. 이때 A는 물체 밑면의 넓이이다. 물체 윗면의 압력은 아래로 향하는 힘을 만드는데 이는 PbotA와 같다. 이 두 가지 힘에 의해 나타나는 것이 부력 [math]\displaystyle{ \vec{B} }[/math]이며 크기는 다음과 같이 나타낼 수 있다.
[math]\displaystyle{ B = \left({P}_{bot} - {P}_{top} \right)A = \left({\rho }_{fluid}gh \right)A }[/math]
“ [math]\displaystyle{ B = {\rho }_{fluid}gh{V}_{disp} }[/math] “
여기서 [math]\displaystyle{ {V}_{disp} = Ah }[/math]는 물체에 의하여 밀려난 유체의 부피이다. [math]\displaystyle{ {\rho }_{fluid}{V}_{disp} }[/math]는 물체에 의해 밀려난 유체의 질량과 같으므로
B = Mg
가 되는에 여기서 Mg는 물체의 의해 밀려난 유체의 무게이다.
유체 동역학[편집 | 원본 편집]
유체의 흐름은 두 유형 중 하나로 설명할 수 있다.
각각의 입자가 매끄러운 경로를 따라 이동하며 다른 입자들의 결로와 교차되지 않는 경우, 이러한 유체의 흐름을 정상류 또는 층흐름이라 한다.
어떤 한계 속력 이상에서는 유체의 흐름이 난류가 된다. 난류는 작은 소용돌이로 대표되는 비정상류이다.
실제로 유체의 운동은 복잡하여 완벽하게 설명할 수 없기 때문에 이상 유체라는 모형을 사용하는데 이 이상 유체는 다음의 네 가지 가정을 만족한다.
1.비점성 유체: 내부 마찰력을 무시한다. 물체는 점성력을 받지 않고 유체를 통과한다.
2. 정상류(steady): 한 지점을 통과하는 모든 입자들의 속도가 같다.
3. 비압축성(incompressible): 유체의 밀도는 항상 일정하게 유지된다고 가정한다.
4. 비회전성 흐름(irrotational): 유체가 어느 한 점에 대해서도 각운동량을 갖고 있지 않다면 유체의 흐름은 비회전성이다.
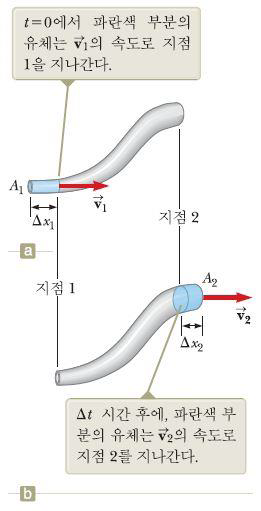
이 그림처럼 크기가 일정하지 않은 관을 흐르는 이상 유체를 생각해보자. a의 파란색 부분에 있는 유체의 질량은 [math]\displaystyle{ {m}_{1} = \rho {A}_{1}\Delta {x}_{1} = \rho {A}_{1}{v}_{1}\Delta t }[/math]이다. 여기서 ρ는 이상유체의 밀도이다. 같은방법으로 b의 파란색부분에 있는 유체의 질량은 [math]\displaystyle{ {m}_{2} = \rho {A}_{2}\Delta {x}_{2} = \rho {A}_{2}{v}_{2}\Delta t }[/math]이다. 그러나 유체가 비압축성이고 흐름이 정상류이기 때문에 Δt 동안 지점1을 통과한 유체의 질량과 같은시간동안 지점2를 통과한 유체의 질량은 같아야 한다. 즉 [math]\displaystyle{ {m}_{1} = {m}_{2} }[/math], 또는 [math]\displaystyle{ \rho {A}_{1}{v}_{1}\Delta t = \rho {A}_{2}{v}_{2}\Delta t }[/math]</math>이다. 따라서
[math]\displaystyle{ {A}_{1}{v}_{1} = {A}_{2}{v}_{2} = }[/math] 일정
이고, 이 식을 유체의 연속 방정식이라고 한다.
베르누이 방정식[편집 | 원본 편집]
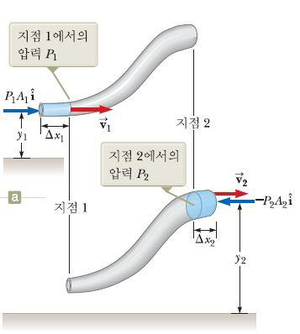
유체가 어떤 영역을 통과하는 동안 속력이 변하거나 지표로부터 고도가 변하게 되면, 유체의 압력 또한 이러한 변화에 따라서 같이 변하게 된다. 유체의 속력과 압력 그리고 고도 사이의 관계는 1738년 스위스의 물리학자 베르뉘에 의해서 처음으로 유도되었다. 이 그림과 같이 균일하지 않은 관을 통해 Δt 시간 동안 이동하는 유체의 한부분을 생각해 보자.
유체가 a에 있는 파란색 부분의 왼쪽에 작용하는 힘의 크기는 P1A1이다. 이 힘이 Δt 동안 이 부분에 한 일은 [math]\displaystyle{ {W}_{1} = {F}_{1}\Delta {x}_{1} = {P}_{1}{A}_{1}\Delta {x}_{1} = {P}_{1}V }[/math] 이며 b에 있는 파란색 부분에서 같은시간동안 한 일은 [math]\displaystyle{ {W}_{2} = {F}_{2}\Delta {x}_{2} = -{P}_{2}{A}_{2}\Delta {x}_{2} = -{P}_{2}V }[/math] 이다. 여기서 V는 파란색 부분의 부피이며 a와b의 파란색 부분의 부피는 같다. W2에서 음의 값이 나오는 것은 유체 부분에 작용하는 힘은 왼쪽 방향이고, 힘의 작용점의 변위는 오른쪽 방향이기 때문이다. 따라서 Δt 동안 이들 힘이 유체에 한 알짜일은
[math]\displaystyle{ W = \left({P}_{1} - {P}_{2} \right)V }[/math]
이다. 이 일의 일부는 유체의 운동에너지를 변화시키고 남은 일부는 유체-지구 계의 중력 위치 에너지를 변화시킨다. 회색부분의 운동에너지 Kgray는 a,b 에서 같다. 따라서 유체의 운동 에너지 변화는
[math]\displaystyle{ \Delta K = \left(\frac{1}{2}m{{v}_{2}}^{2} + {K}_{gray} \right) - \left(\frac{1}{2}m{{v}_{1}}^{2} + {K}_{gray} \right) = \frac{1}{2}m{{v}_{2}}^{2} - \frac{1}{2}m{{v}_{1}}^{2} }[/math]
이다. 그리고 유체의 중력 위치에너지 변화는
[math]\displaystyle{ \Delta U = \left(mg{y}_{2} + {U}_{gray} \right) - \left(mg{y}_{1} + {U}_{gray} \right) = mg{y}_{2} - mg{y}_{1} }[/math]
[math]\displaystyle{ W = \Delta K + \Delta U }[/math]이므로 대입하면
[math]\displaystyle{ \left({P}_{1} - {P}_{2} \right)V = \frac{1}{2}m{{v}_{2}}^{2} - \frac{1}{2}m{{v}_{1}}^{2} + mg{y}_{2} - mg{y}_{1} }[/math]
[math]\displaystyle{ {P}_{1} - {P}_{2} = \frac{1}{2}\rho {{v}_{2}}^{2} - \frac{1}{2}\rho {{v}_{1}}^{2} + \rho g{y}_{2} - \rho g{y}_{1} }[/math]
[math]\displaystyle{ {P}_{1} + \frac{1}{2}\rho {{v}_{1}}^{2} + \rho g{y}_{1} = {P}_{2} + \frac{1}{2}\rho {{v}_{2}}^{2} + \rho g{y}_{2} }[/math]
이다. 이 식이 이상 유체에 적용되는 베르누이 방정식이다. 이 식은 때때로 다음과 같이 나타내기도 한다.
“ [math]\displaystyle{ P + \frac{1}{2}\rho {v}^{2} + \rho gy = }[/math]일정 “
각주
- ↑ 부력