잔글 (문자열 찾아 바꾸기 - "{{학술}}" 문자열을 "" 문자열로) |
잔글편집 요약 없음 |
||
| 1번째 줄: | 1번째 줄: | ||
'''우산 정리'''는 [[삼각형]]과 그 외접원에 관한 [[수학 정리]] 중 하나다. 곱하는 선분의 모양이 마치 [[우산]]처럼 생겨서 우산 정리라 부른다. 사실 대한민국]]에서만 존재하는 정리로, 다른 나라에서는 이 정리를 부르는 특별한 이름은 없다. | |||
[[삼각형]]과 그 외접원에 관한 정리 중 | |||
== 정리 == | == 정리 == | ||
| 28번째 줄: | 25번째 줄: | ||
세 경우 중 내각의 이등분선의 경우엔 <math>\angle{EBC}=\angle{EAC}=\angle{EAB}=\angle{ECB}</math>이므로 <math>\triangle{EBC}</math>는 [[이등변삼각형]]이 된다. 따라서 <math>\overline{EB}=\overline{EC}</math>. 이제 <math>\triangle{EBC}</math>에서 우산 정리를 쓰면, <math>\overline{EB}\cdot\overline{EC}=\overline{ED}\cdot\overline{EA}</math>가 되고, 따라서 <math>\overline{EB}^2=\overline{ED}\cdot\overline{EA}=\overline{EC}^2</math>가 된다. 이는 곧 할선과 접선에 대한 [[방멱의 정리]]가 성립함을 의미하고, <math>\triangle{ABD},\,\triangle{ACD}</math>의 외접원을 각각 그렸을 때, <math>\overline{EB},\,\overline{EC}</math>가 각 외접원의 접선이 됨을 알 수 있다. 이걸 자세하게 설명하는 이유는 바로 이 정리가 [[반전 기하]]의 토대가 되기 때문이다. 또한 <math>\triangle{ABD}\sim\triangle{CED}</math>를 유도 가능한데, 여기에서는 두 현에 대한 [[방멱의 정리]]가 나온다. | 세 경우 중 내각의 이등분선의 경우엔 <math>\angle{EBC}=\angle{EAC}=\angle{EAB}=\angle{ECB}</math>이므로 <math>\triangle{EBC}</math>는 [[이등변삼각형]]이 된다. 따라서 <math>\overline{EB}=\overline{EC}</math>. 이제 <math>\triangle{EBC}</math>에서 우산 정리를 쓰면, <math>\overline{EB}\cdot\overline{EC}=\overline{ED}\cdot\overline{EA}</math>가 되고, 따라서 <math>\overline{EB}^2=\overline{ED}\cdot\overline{EA}=\overline{EC}^2</math>가 된다. 이는 곧 할선과 접선에 대한 [[방멱의 정리]]가 성립함을 의미하고, <math>\triangle{ABD},\,\triangle{ACD}</math>의 외접원을 각각 그렸을 때, <math>\overline{EB},\,\overline{EC}</math>가 각 외접원의 접선이 됨을 알 수 있다. 이걸 자세하게 설명하는 이유는 바로 이 정리가 [[반전 기하]]의 토대가 되기 때문이다. 또한 <math>\triangle{ABD}\sim\triangle{CED}</math>를 유도 가능한데, 여기에서는 두 현에 대한 [[방멱의 정리]]가 나온다. | ||
== | == 같이 보기 == | ||
*[[삼각형]] | *[[삼각형]] | ||
*[[각의 이등분선 정리]] | *[[각의 이등분선 정리]] | ||
{{각주}} | |||
[[분류:기하학]] | [[분류:기하학]] | ||
[[분류:수학 정리]] | |||
2018년 2월 24일 (토) 19:36 판
우산 정리는 삼각형과 그 외접원에 관한 수학 정리 중 하나다. 곱하는 선분의 모양이 마치 우산처럼 생겨서 우산 정리라 부른다. 사실 대한민국]]에서만 존재하는 정리로, 다른 나라에서는 이 정리를 부르는 특별한 이름은 없다.
정리
|
|
|
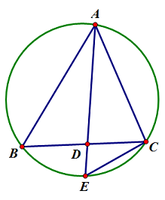
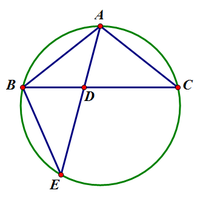
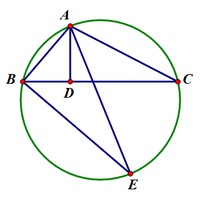
| 내각의 이등분선 | 이등변삼각형 | [math]\displaystyle{ \overline{AE} }[/math]가 지름, [math]\displaystyle{ \overline{AD} }[/math]는 수선 |
증명
내각의 이등분선일 경우
[math]\displaystyle{ \angle{BAD}=\angle{EAC} }[/math](내각의 이등분), [math]\displaystyle{ \angle{ABD}=\angle{AEC} }[/math](호 [math]\displaystyle{ \overarc{AC} }[/math]에 대한 원주각)이므로 [math]\displaystyle{ \triangle{ABD}\sim\triangle{AEC} }[/math]이다. 따라서 [math]\displaystyle{ \overline{AB}:\overline{AD}=\overline{AE}:\overline{AC} }[/math]이고, 이는 곧, [math]\displaystyle{ \overline{AB}\cdot\overline{AC}=\overline{AD}\cdot\overline{AE} }[/math]이다.
이등변삼각형일 경우
[math]\displaystyle{ \angle{ABC}=\angle{ACB}=\angle{BEA} }[/math](이등변삼각형과 원주각의 성질), [math]\displaystyle{ \angle{BAE} }[/math] 공통 이므로 [math]\displaystyle{ \triangle{ABD}\sim\triangle{AEB} }[/math] (AA 닮음). 따라서 [math]\displaystyle{ \overline{AB}:\overline{AE}=\overline{AD}:\overline{AB} }[/math]이고, 곧 [math]\displaystyle{ \overline{AD}\cdot\overline{AE}=\overline{AB}^2=\overline{AB}\cdot\overline{AC} }[/math]이다.
지름과 수선의 경우
[math]\displaystyle{ \overline{AE} }[/math]가 지름이므로, [math]\displaystyle{ \angle{ABE}=90^\circ }[/math]이다. 또한, [math]\displaystyle{ \angle{ACD}=\angle{AEB} }[/math](원주각)이므로, [math]\displaystyle{ \triangle{ADC}\sim\triangle{ABE} }[/math] (AA 닮음). 따라서 [math]\displaystyle{ \overline{AD}:\overline{AB}=\overline{AC}:\overline{AE} }[/math]이고, 곧 [math]\displaystyle{ \overline{AB}\cdot\overline{AC}=\overline{AD}\cdot\overline{AE} }[/math]이다.
기타
세 경우 중 내각의 이등분선의 경우엔 [math]\displaystyle{ \angle{EBC}=\angle{EAC}=\angle{EAB}=\angle{ECB} }[/math]이므로 [math]\displaystyle{ \triangle{EBC} }[/math]는 이등변삼각형이 된다. 따라서 [math]\displaystyle{ \overline{EB}=\overline{EC} }[/math]. 이제 [math]\displaystyle{ \triangle{EBC} }[/math]에서 우산 정리를 쓰면, [math]\displaystyle{ \overline{EB}\cdot\overline{EC}=\overline{ED}\cdot\overline{EA} }[/math]가 되고, 따라서 [math]\displaystyle{ \overline{EB}^2=\overline{ED}\cdot\overline{EA}=\overline{EC}^2 }[/math]가 된다. 이는 곧 할선과 접선에 대한 방멱의 정리가 성립함을 의미하고, [math]\displaystyle{ \triangle{ABD},\,\triangle{ACD} }[/math]의 외접원을 각각 그렸을 때, [math]\displaystyle{ \overline{EB},\,\overline{EC} }[/math]가 각 외접원의 접선이 됨을 알 수 있다. 이걸 자세하게 설명하는 이유는 바로 이 정리가 반전 기하의 토대가 되기 때문이다. 또한 [math]\displaystyle{ \triangle{ABD}\sim\triangle{CED} }[/math]를 유도 가능한데, 여기에서는 두 현에 대한 방멱의 정리가 나온다.