편집 요약 없음 |
편집 요약 없음 |
||
| 2번째 줄: | 2번째 줄: | ||
[[분류:컴퓨터_프로그래밍]] | [[분류:컴퓨터_프로그래밍]] | ||
[[분류:수학인듯 과학아닌 공학같은 컴퓨터과학]] | [[분류:수학인듯 과학아닌 공학같은 컴퓨터과학]] | ||
이 시리즈에서 알고리즘을 설명하기 위하여 나오는 모든 코드는 '''[[C(프로그래밍 언어)|C언어]]''' 또는 [[C++]], 또는 부분적으로 [[Python]]을 사용한다. 다른 언어들은 추가 바람! | |||
== 들어가기 전 == | == 들어가기 전 == | ||
| 151번째 줄: | 153번째 줄: | ||
프로그래밍 대회에서 문제를 풀 때에는 프로그램 수행 시간의 제한이 있기 때문에, 일정한 시간 복잡도 이하가 되어야 정답, 즉 Accepted 판정이 된다. 이 때 필요한 시간 복잡도를 대략 계산해 보려면 문제에서 <math>N</math>의 제한을 보면 된다. 당신이 짠 프로그램의 시간 복잡도에 실제 <math>N</math>의 제한을 넣어 보자. 이 수가 대략 1천만 ~ 10억<ref>상수가 다양할 수 있으므로 이의 범위를 넓게 잡았다.</ref> 사이일 때 대략 1초의 시간 제한에 맞는 프로그램이라 할 수 있다. | 프로그래밍 대회에서 문제를 풀 때에는 프로그램 수행 시간의 제한이 있기 때문에, 일정한 시간 복잡도 이하가 되어야 정답, 즉 Accepted 판정이 된다. 이 때 필요한 시간 복잡도를 대략 계산해 보려면 문제에서 <math>N</math>의 제한을 보면 된다. 당신이 짠 프로그램의 시간 복잡도에 실제 <math>N</math>의 제한을 넣어 보자. 이 수가 대략 1천만 ~ 10억<ref>상수가 다양할 수 있으므로 이의 범위를 넓게 잡았다.</ref> 사이일 때 대략 1초의 시간 제한에 맞는 프로그램이라 할 수 있다. | ||
만약, 당신이 짠 프로그램의 시간 복잡도가 <math>O(n^2\log n)</math>이고, <math>n</math>의 제한이 <math>n\le 1,000</math>이라고 하자. 이 때 <math>n</math>의 제한인 1,000을 실제로 식에 넣어보는 것이다. <math>1000^2\log 1000 = 10,000,000</math><ref>컴퓨터과학에서는 로그 2를 상용로그로 쓴다.</ref>이므로, 상수가 너무 크지 않으면, 즉 안에 들어가 있는 계산량이 너무 많지 않은 이상은 1초의 시간 제한 안에 돌아가게 될 것이다. | 만약, 당신이 짠 프로그램의 시간 복잡도가 <math>O(n^2\log n)</math>이고, <math>n</math>의 제한이 <math>n\le 1,000</math>이라고 하자. 이 때 <math>n</math>의 제한인 1,000을 실제로 식에 넣어보는 것이다. <math>1000^2\log 1000 = 10,000,000</math><ref>컴퓨터과학에서는 로그 2를 상용로그로 쓴다.</ref>이므로, 상수가 너무 크지 않으면, 즉 안에 들어가 있는 계산량이 너무 많지 않은 이상은 1초의 시간 제한 안에 돌아가게 될 것이다. | ||
== 플로우 차트 == | == 플로우 차트 == | ||
2015년 12월 8일 (화) 17:17 판
이 시리즈에서 알고리즘을 설명하기 위하여 나오는 모든 코드는 C언어 또는 C++, 또는 부분적으로 Python을 사용한다. 다른 언어들은 추가 바람!
들어가기 전
일단 이게 입문인지부터 생각해보자
빨간 컵에 칠성사이다가 담겨져 있고 파란 컵에 스프라이트가 담겨져 있다. 여기서 파란 컵에 칠성사이다를 넣고 빨간 컵에 스프라이트를 넣을려면 어떻게 해야 될까? 해답은 간단하다. 다른 컵(여기선 노란 컵이라 하겠다.)에 빨간 컵의 칠성사이다를 노란 컵에 붓고 빨간 컵이 비게 되면 파란 컵의 스프라이트를 빨간 컵에 붓고 파란 컵이 비게 되면 노란 컵에 담았던 칠성사이다를 파란 컵에 부으면 된다. 갑자기 노란 컵이 튀어나와서 쌩뚱맞다고 생각하는 사람이 있을 수 있겠지만 다른 컵을 쓰면 안된다고는 안했다. 알고리즘은 문제를 해결하기 위한 것이지 수수께끼나 넌센스 문제가 아니다.
이 이야기가 왜 나왔냐면 프로그래밍을 할 때 아래 소스처럼 2개의 변수 값을 서로 바꿀 경우 변수 2개 가지고 끙끙 거리지 말고 간단하게 변수 하나 더 사용해서 쉽게 해결하면 되기 때문이다. 이제 제 3의 변수를 쓰지 않고 변수 2개의 값을 맞바꾸는 알고리즘을 생각해보자.
| 의사코드 펼치기 |
|---|
1 function 바꾸기(첫번째컵, 두번째컵): 2 잠시담아둘컵 ← 첫번째컵 3 첫번째컵 ← 두번째컵 4 두번째컵 ← 잠시담아둘컵 5 end function 6 7 function 지금상황(): 8 파란컵 ← "칠성사이다" 9 빨간컵 ← "스프라이트" 10 바꾸기(파란컵, 빨간컵) 11 print 파란컵 12 print 빨간컵 13 end function |
using System;
namespace 사이다컵바꾸기
{
class Program
{
static void Main(string[] args)
{
// 빨간 컵과 파란 컵에 칠성사이다와 스프라이트가 담겨져 있다.
string 빨간컵 = "칠성사이다";
string 파란컵 = "스프라이트";
Console.WriteLine("=====바꾸기 전=====");
Console.WriteLine("빨간컵 : {0}", 빨간컵);
Console.WriteLine("파란컵 : {0}", 파란컵);
// 새롭게 준비한 노란 컵
string 노란컵;
// 스프라이트를 빨간 컵에 붓기 위해 칠성사이다를 노란컵에 붓는다.
// 그 다음 파란 컵의 스프라이트를 빨간 컵에 붓는다.
// 그 다음 노란 컵에 임시로 담아둔 칠성 사이다를 파란 컵에 붓는다.
노란컵 = 빨간컵;
빨간컵 = 파란컵;
파란컵 = 노란컵;
Console.WriteLine("=====바꾼 후=====");
Console.WriteLine("빨간컵 : {0}", 빨간컵);
Console.WriteLine("파란컵 : {0}", 파란컵);
}
}
}
여담으로, 위 취소선의 답은 의외로 간단하다. 정수가 저장되어 있는 a와 b가 있을 때, a와 b를 더한 다음 a에 저장한다. 그 다음 a에서 b를 뺀 값(즉 원래 a값)을 b에 저장한다. 그 다음 a에서 b를 뺀 값을 a에 저장하면 된다. 숫자가 아니고 객체면? 음료수는 더하고 빼면 섞이잖아 하지만 이 방법은 산술 오버플로우의 문제 때문에 자료형이 표현 가능한 범위보다 더 적은 범위의 변수만 바꿀 수 있다.
사실 덧셈보다 더 빠른 방법은 XOR 회로를 사용하는법이 있다. 값이 같지 않으면 a=a^b b=a^b a=a^b를 넣어두면 정수가 아니더라도, 산술적 연산이 아니라 비트 배열 자체가 바뀌기 때문에 값이 교환된다.하지만 병렬 프로그래밍에서는 무리DA☆ZE★ 하지만, 컴퓨터의 최적화 정도에 따라서 그냥 노란 컵을 이용하는 방법이 더 빠를 수도 있다.
왜 알아야 하나?
프로그램을 통해 구하는 결과를 '건물'이라고 치면, 알고리즘은 '설계도'라고 할 수 있다. 이 한 마디로 알고리즘의 중요성에 대해서는 더 이상의 설명은 생략한다.
다만, 건물을 짓는데 다양한 방법이 동원되는 것처럼 알고리즘도 다양하게 적용될 수 있다. 결과가 동일하더라도 사용하는 알고리즘에 따라 프로그램의 속도나 처리방식 등이 크게 차이나는 경우도 있다. 그에 대한 설명은 아래를 참조.
시간 복잡도
방을 정리한다고 해보자. 방에 널려 있는 물건의 양에 따라 정리에 걸리는 시간이 달라질 것이다. 프로그램을 작성할 때에도 입력의 크기에 따라서 프로그램이 계산하는 횟수가 크게 달라진다. 입력된 자료의 양과 알고리즘 실행에 걸리는 시간 사이에는 어느 정도의 관계가 있다. 이것을 알고리즘의 시간 복잡도라 한다.
이해하기 쉽게 하기 위해서 한 가지 프로그램으로 예를 들어보자. 아래 두 프로그램은 자연수 N이 주어졌을 때 1부터 N까지의 합을 구하는 프로그램들이다.
[소스 1]
#include <cstdio>
int main(void)
{
int N, res = 0;
scanf("%d", &N);
for (int i=1; i<=N; i++) {
res += i;
}
printf("%d\n", res);
return 0;
}
[소스 2]
#include <cstdio>
int main(void)
{
int N, res;
scanf("%d", &N);
res = N * (N+1) / 2;
printf("%d\n", res);
return 0;
}
소스 1에서는 for문을 활용하여 직접 res에 1에서 N까지를 더해서 합을 계산했다. 그리고 소스 2에서는 1에서 N까지 자연수들의 합은 [math]\displaystyle{ \frac{n(n+1)}{2} }[/math]인 수학 공식을 이용하여 합을 계산했다. 소스 1의 경우에는 [math]\displaystyle{ N = 1,000 }[/math]이라면 덧셈이 1,000번 일어나고, [math]\displaystyle{ N = 1,000,000 }[/math]이라면 덧셈이 1,000,000번 일어나게 된다. 계산하는 횟수가 [math]\displaystyle{ N }[/math]에 비례하는 것이다. 반면에, 소스 2에서는 [math]\displaystyle{ N = 1,000 }[/math]이든, [math]\displaystyle{ N = 1,000,000 }[/math]이든 무조건 덧셈 한 번과 곱셈 한 번, 나눗셈 한 번만을 하게 된다. [math]\displaystyle{ N }[/math]에 아무 관계 없는 상수 시간 안에 계산이 처리되는 것이다.
모든 알고리즘은 이와 같이 입력되는 데이터의 크기 또는 갯수에 따라 이의 계산 횟수[1]수행 시간이 크게 달라지게 된다. 입력받는 데이터의 크기에 따른 알고리즘의 수행시간의 변화가 시간복잡도이다. 시간복잡도가 더 큰 알고리즘들은 더 큰, 혹은 많은 데이터를 처리할 때 훨씬 더 오랜 시간이 걸리게 된다. 그런데 이 계산 횟수의 정확한 측정이 어렵기 때문에, 보통 Big O 표기법이라는 걸 이용해서 표시한다.
입력된 데이터의 갯수가 [math]\displaystyle{ n }[/math]개일 때 [math]\displaystyle{ 2n+7 }[/math]번 계산하는 알고리즘과 [math]\displaystyle{ 2n }[/math]번 계산하는 알고리즘이 있다고 하자. [math]\displaystyle{ n }[/math]이 커지면 둘 사이의 차이는 사실상 없어진다. 이를 O 표기법으로 나타내면 [math]\displaystyle{ O(2n+7)=O(2n) }[/math]이다. 대략 O 표기법은 상수만큼의 시간 차이는 무시하는 것이라고 생각할 수 있겠다. [2]
크기 n의 데이터가 들어올 때 [math]\displaystyle{ n^2 }[/math]번 계산해서 답을 내는 알고리즘과 [math]\displaystyle{ 1,000n }[/math]번 계산해서 답을 내는 알고리즘을 비교해 보자. [math]\displaystyle{ n=10 }[/math]일 때는 [math]\displaystyle{ 1,000n }[/math]번 계산하는 알고리즘이 100배 더 느릴지 모르지만, [math]\displaystyle{ n=1,000 }[/math]만 되어도 두 알고리즘의 속도가 비슷해지고, [math]\displaystyle{ n=100,000 }[/math]인 경우에는 [math]\displaystyle{ n^2 }[/math]번 계산하는 알고리즘이 100배나 더 느려진다. [math]\displaystyle{ n=10 }[/math] 정도의 작은 데이터에서는 100배 더 느리다고 해도 불과 0.0001초 정도밖에 차이가 나지 않을 것이다. 데이터의 크기가 적으므로 두 프로그램 모두 매우 빠르기 때문이다! 하지만 [math]\displaystyle{ n=100,000 }[/math]에서는 100배의 차이는 생각하는 것만큼 매우 크다. [math]\displaystyle{ 1000n }[/math]번 계산하는 프로그램이 0.3초간 계산해서 답을 내놓는 사이에, [math]\displaystyle{ n^2 }[/math]번 계산하는 프로그램은 30초는 생각해야 답을 내놓을 수 있을 것이다. [math]\displaystyle{ n=1,000,000 }[/math]라던지, [math]\displaystyle{ n=10,000,000 }[/math]와 같은 식으로 n이 더더욱 커지면 어떻게 될까? 두 프로그램의 시간 차이는 기하급수적으로 커지게 될 것이다. 위의 예시에서 알 수 있었던 것은 계산 횟수에 붙은 상수는 별로 중요하지 않다는 것이다. 1,000이라는 상수가 무색해질 정도로 n이 커지면, 그 때는 n이 커짐에 따라 증가하는 계산 횟수가 훨씬 더 중요해진다.[3] 그래서 시간복잡도를 나타낼 때에는 상수는 모두 떼어버리기로 하자. [math]\displaystyle{ n }[/math]번 계산하든, [math]\displaystyle{ 7n+1312 }[/math]번 계산하든, [math]\displaystyle{ 142857n }[/math]번 계산하든 모두 [math]\displaystyle{ O(n) }[/math]로 나타내는 것이다! 이와 비슷하게, [math]\displaystyle{ 3^n+2n^3+12451n^2+33n\log n+151511 }[/math]번 계산하는 알고리즘의 시간 복잡도는 [math]\displaystyle{ O(2^n) }[/math][4]로 나타낼 수 있다.
위의 소스들의 시간 복잡도는 어떻게 쓸 수 있을까? 소스 1은 [math]\displaystyle{ O(N) }[/math]의 시간 복잡도를, 소스 2는 [math]\displaystyle{ O(1) }[/math]의 시간 복잡도를 가지게 된다는 것을 알 수 있다. 직관적으로도 알 수 있듯이, [math]\displaystyle{ O(1) }[/math]의 알고리즘이 [math]\displaystyle{ O(N) }[/math]의 알고리즘보다 더 빠른 알고리즘이라고 할 수 있다.
자주 등장하는 알고리즘의 시간 복잡도는 아래와 같다. 위의 알고리즘이 가장 시간 복잡도가 낮은, 즉 가장 빠른 알고리즘이라고 부르고, 아래의 알고리즘이 가장 시간 복잡도가 높은, 즉 가장 느린 알고리즘이라 부른다.
| 시간 복잡도 | 설명 |
|---|---|
| [math]\displaystyle{ O(1) }[/math] | 상수 형태. n의 값에 상관없이 일정한 양의 계산만 한다. |
| [math]\displaystyle{ O(\log n) }[/math] | 로그 형태 |
| [math]\displaystyle{ O(n) }[/math] | 선형 |
| [math]\displaystyle{ O(n\log n) }[/math] | 선형로그 형태 |
| [math]\displaystyle{ O(n^2), O(n^3),\cdots }[/math] | 다차 형태 |
| [math]\displaystyle{ O(2^n) }[/math] | 지수 형태 |
| [math]\displaystyle{ O(n!) }[/math] | 팩토리얼 형태 |
예를 들어 아래의 링크드 리스트에서 특정 값을 찾는데 걸리는 평균 시간 복잡도는 [math]\displaystyle{ O(n) }[/math], 해시 테이블에서 특정 값을 찾는데 걸리는 평균 시간 복잡도는 [math]\displaystyle{ O(1) }[/math]이다. 이는 평균적으로 해시 테이블에서의 탐색이 링크드 리스트에서의 탐색보다 빠르다는 뜻이다.
프로그래밍 대회에서 문제를 풀 때에는 프로그램 수행 시간의 제한이 있기 때문에, 일정한 시간 복잡도 이하가 되어야 정답, 즉 Accepted 판정이 된다. 이 때 필요한 시간 복잡도를 대략 계산해 보려면 문제에서 [math]\displaystyle{ N }[/math]의 제한을 보면 된다. 당신이 짠 프로그램의 시간 복잡도에 실제 [math]\displaystyle{ N }[/math]의 제한을 넣어 보자. 이 수가 대략 1천만 ~ 10억[5] 사이일 때 대략 1초의 시간 제한에 맞는 프로그램이라 할 수 있다. 만약, 당신이 짠 프로그램의 시간 복잡도가 [math]\displaystyle{ O(n^2\log n) }[/math]이고, [math]\displaystyle{ n }[/math]의 제한이 [math]\displaystyle{ n\le 1,000 }[/math]이라고 하자. 이 때 [math]\displaystyle{ n }[/math]의 제한인 1,000을 실제로 식에 넣어보는 것이다. [math]\displaystyle{ 1000^2\log 1000 = 10,000,000 }[/math][6]이므로, 상수가 너무 크지 않으면, 즉 안에 들어가 있는 계산량이 너무 많지 않은 이상은 1초의 시간 제한 안에 돌아가게 될 것이다.
플로우 차트
기호
자료구조
데이터를 저장하는 방식을 말한다. 수많은 자료구조 중 데이터에 맞는 특성을 지닌 자료구조를 선택하는 것은 효율적인 알고리즘 작성에 반드시 필수적이다.
선형 자료구조
한 종류의 데이터가 선처럼 길게 나열된 자료구조이다.
랜덤 접근 가능
모든 자료에 O(1)으로 접근이 보장되는 자료구조들이다.
배열
가장 쉬운 자료구조이자 언어에 따라 활용법이 가장 크게 달라지는 자료구조. C언어에서는 대괄호를 사용한다.
int array1[]; //int *array1과 비슷함.
int array2[10]; //크기를 가지는 배열
int array3[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; //초기화한 배열
C에서 배열에 포인터를 사용하여 접근하는 것을 보면, 배열의 각 원소의 주소가 연속적으로 배치되어 있다는 것을 알 수 있다.
파이썬에서는 그냥 리스트 자료구조를 사용한다.
array1 = [] # 빈 리스트.
array2 = [0, 1, 2, 3, 4] # 길이가 5인 리스트. C언어나 파이썬은 숫자를 0부터 센다.
array3 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # 리스트 안에 리스트가 중첩되어 있다.
# 리스트 안에는 리스트를 포함하여 어떤 객체도 넣을 수 있다.
해시
해시는 해시 함수로 구현한다. 해시 함수는 마치 배열처럼, 어떤 자료를 찾을 때 [math]\displaystyle{ O(1) }[/math]의 시간만을 소요한다. 해시함수에 키 값을 넣어 주소값을 얻고, 그 주소에 위치한 버킷에 저장된 데이터를 가져오는 방식을 사용한다. 하지만, 언제나 [math]\displaystyle{ O(1) }[/math]이 보장되는 것은 아니다. 자세한 것은 해시 테이블 참고.
파이썬의 해시는 “딕셔너리”(Dictionary)라고 부른다.
dict1 = {1:"하나", "apple":"사과", "리스트":[1, 2, 3]}
랜덤 접근 불가능
모든 자료에 O(1)으로 접근이 보장되지 않는 자료구조들이다.
스택
먼저 들어간 자료가 나중에 나오는 자료구조. 유식한 말로 후입선출(後入先出) 구조라고 한다. 자료를 넣는 push 함수와 자료를 빼는 pop 함수를 갖는 게 정석이다. empty, full 등 다른 함수들을 옵션으로 가질 수도 있다.
아래는 배열로 구현한 스택이다.[7]
//헤더 부분
void push(int); //push 함수 정의
int pop();
//소스 부분
int array[500]; //스택의 최대 크기는 500
int top = -1; //스택의 현재 크기는 0;
void push(int n)
{
top = top + 1; //혹은 top++;
array[top] = n;
}
int pop()
{
int value = array[top];
top = top - 1;
return value;
}
사용법은 스택에 넣고 싶은 것을 push로 넣고, pop로 빼면 된다.
push(1), push(2), push(3);
printf("%d %d %d", pop(), pop(), pop());
출력 결과는 3 2 1과 같을 것이다.
파이썬의 리스트 자료구조로 스택 클래스를 만들면 다음과 같을 것이다.
class stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def peek(self):
return self.items[-1]
def size(self):
return len(self.items)
def pop(self):
return self.items.pop()
이렇게 작성한 스택 클래스로 문자열을 뒤집는 함수를 만들면 다음과 같다.
def reverseString(str):
s = stack()
result = ""
for i in str:
s.push(i)
while s.isEmpty() != True:
result += s.pop()
return result
함수의 실행 결과는 다음과 같다.
>>> print(reverseString("apple"))
elppa
>>>
큐
먼저 들어간 자료가 먼저 나오는 자료구조. 선입선출(先入先出) 구조라고도 한다. 자료를 넣는 Enqueue 함수와 자료를 빼내는 Dequeue 함수를 가진다.
밑의 큐는 연결 리스트로 구현된 큐이다. 배열로 하는 경우에는 보통 순환 큐라고 해서 맨 끝과 앞을 연결(나머지 연산자 % 이용)하는 방식으로 구현한다. 소스는 다음과 같다.
void enqueue(int);
int dequeue();
struct linkedList
{
int value;
struct linkedList *next;
};
struct linkedList *front; //큐의 맨 앞을 가리킨다.
struct linkedList *back; //큐의 맨 뒤를 가리킨다.
void enqueue(int n) //큐에 자료를 넣는 함수
{
if(front == NULL) //큐가 비어 있을 경우
{
*front = {n, NULL}; //맨 앞에 자료를 넣고
back = front; //맨 뒤와 맨 앞을 같게 한다.
}
else
{
back -> *next = {n, NULL}; //맨 뒤 다음에 자료를 넣는다.
back = back -> next; //넣은 자료를 맨 뒤로 한다.
}
}
int dequeue() //큐에서 자료를 빼는 함수
{
int res = front -> value;
front = front -> next;
return res;
}
파이썬에서 리스트 자료구조로 큐를 구현하는 클래스를 작성하자면 다음과 같을 것이다.
class queue:
def __init__(self):
self.items = []
def enqueue(self, item):
self.items.insert(0, item)
def dequeue(self):
return self.items.pop()
def isEmpty(self):
return self.items == []
def size(self):
return len(self.items)
데크
간단하게 말하자면 스택과 큐의 융합형태. 양쪽 끝에서 삽입과 삭제가 모두 가능하다. 보통 입력이나 출력 중 하나를 한 쪽 입구만 가능하게 제한하는 형태가 많이 쓰인다.
링크드 리스트
연결 리스트라고도 불린다. 값과 다음 노드를 가지고 있다. 옵션으로 이전 노드를 가지게 할 수도 있으며, 맨 뒤 노드가 맨 앞 노드를 다음 노드로 가지게 할 수도 있다. 또한, 중간에서 삽입과 삭제를 할 수 있다. 가장 간단하게 구현한 것은 위의 큐. 다시 한 번 뜯어보고 옵션을 넣어본다면 실력 향상에 도움이 될 것이다.
선형구조 자료 탐색법
말 그대로 선형구조로 된 자료를 탐색하는 방법이다. 보통 어떤 값이 어디에 있는지 알아내는 게 목적이다.
순차 탐색
말 그대로 시작점부터 순차적으로 탐색하는 것이다. 전부 탐색한다고 생각할 때,연산량은 O(n)이다.
솔직히 이건 해당 언어만 알면 누구나 코드를 만들어낼 수 있을 수준이기에,소스 코드 부분은 생략한다.
이분 탐색
특수한 상황에서 순차 탐색보다 좀 더 빠른 속도를 기대할 수 있는 알고리즘으로,연산량은 O(log2 N)이다. 이분 탐색이란,순차 탐색과 달리 가운데에서 시작해서 매번 일정한 조건에 따라 어떤 방향의 가운데 값으로 탐색할 지 결정하는 알고리즘이다.이 때 가운데 값이란 평균이 아니고 중간값이다. 이를 좀 더 자세히 설명하자면 이렇다. 배열 1 3 4 7 8 13 17에서 '8'이 있는 위치를 찾는다고 가정하자.
배열: 1 3 4 7 8 13 17
1st:총 배열의 가운데인 7을 선택.
7<8 이므로 더 큰 숫자가 있는 오른쪽으로 진행.
2nd:7~17의 배열중 가운데인 13을 선택.
13>8 이므로 더 작은 숫자가 있는 왼쪽으로 진행.
3rd:7과 13의 가운데에 있는 8을 선택.
8=8 이고 배열은 5번째이므로 답은 5이다.
단,이를 위해서는 특수한 기준으로 정렬되어 있어야 한다. 정렬법에 대해서는 아래쪽 확인. 아래의 소스에서는 모든 입력코드가 오름차순으로 정렬되어 있다고 가정한다.
//헤더 부분
int solve(int,int);
//소스 부분
int A[500]; //총 500개까지 담을 수 있는 배열에서 탐색.
int k; //탐색할 값.
int solve(int s, int e);
{
int m;
while(e-s>=0)
{
m=(s+e)/2; //값이 있을 가능성이 있는 값의 가운데 값.
if(A[m]==k)
return m+1; //그 값이 만약 탐색할 값이면 그 위치를 리턴.
if(A[m]<k) s=m+1; //만약 A[m]이 작으면 좀 더 큰 값들이 있는 오른쪽이 탐색되도록 변경.
else e=m-1; //아까와 정반대.
}
return -1; //찾는 값이 없을 경우 -1을 준다.
}
이것을 변형하면,배열의 어디부터가 어떤 숫자 이상인지 혹은 초과인지 알 수 있다.
전자가 Lower bound,후자가 Upper bound이다. 이들은 아예 <algorithm>에 포함된 함수가 있으니 한번 봐두자.
//헤더
#include<algorithm>
//.h는 붙이지 않는다.
//소스,A가 배열이고 배열의 데이터 개수는 n개,찾는 데이터는 k.
std::lower_bound(A,A+n,k,[compare])
std::upper_bound(A,A+n,k,[compare])
//[compare]은 비교 기준이며,이게 생략된 경우 오름차순이라고 간주한다.
비선형 자료구조
선형 자료구조가 아닌 모든 자료구조이다. 다만,사전적인 정의를 하자면 i 번째 값을 탐색한 뒤의 i+1이 정해지지 않은 구조를 의미한다.
그래프
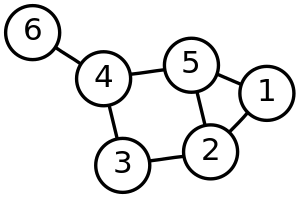
함수의 그래프와는 전혀 다르다. 고등학교 교육과정에서 이산수학이 빠지고 행렬도 빠짐에 따라 같이 빠지게 되는 비운의 단원 알고리즘을 배우다 보면 자주 나오는 구조로, 점들, 그리고 점들을 연결하는 선들만으로 이루어진 지도 비스무리한 걸 연상하면 편하다. 이때의 점을 정점(vertex), 선을 간선(edge)이라고 부른다.[8] 간단한 구조체를 만들어 보자.
struct Edge //정점보다는 간선으로 나타내는 편이 대부분의 경우에 더 좋다.
{
int snode; //시작 정점
int enode; //종료 정점
//int cost; //가중치를 가지는 간선에 사용된다.
};
위의 struct Edge가 하나 이상 있는 것이 바로 그래프이다.
그래프를 다르게 구현하는 경우도 있는데,바로 인접 행렬로 구현하는 방법과 인접 리스트로 구현하는 방법이다.
다음은 데이터를 받아서 저장하는 가중치 그래프라고 가정하자. 이 경우는 인접 행렬로 구성하는 방법이다.
#include<stdio.h>
int m,g[101][101]; //정점은 최대 100개
int main()
{
scanf("%d",&m); //간선의 개수
for(int i=0;i<m;i++)
{
int a,b,w //a와 b는 간선이 연결된 곳,w는 가중치
scanf("%d %d %d",&a,&b,&w);
G[a][b]=G[b][a]=w;
}
}
인접 리스트로 구성이 가능하긴 하지만 너무 복잡해서 구현하기 까다롭다. 그래서 그래프도 함수로 정의되어 있다.
//헤더 부분
#include<vector>
std::vector<int> G[101];
//소스 부분
G[i].push_back (x); //i와 x는 연결된 그래프이다.
이 때,탐색시간은 인접 리스트 방식의 구현이 더 짧다.(단,v가 정점이고 e가 간선이라고 가정한다.)
인접 행렬:O(v*e)
인접 리스트:O(v+e)
그래프 관련 용어
- 정점(Vertex)
- 간단하게 말해서, 연결점이다. 좀 더 구체적으로 정의하자면, 여러 가지 특성을 가질 수 있는 객체이다. 즉, 어떤 객체도 정점이 될 수 있다.
- 고립 정점
- 간선이 단 하나도 연결되지 않은 외톨이 정점이다.
- 간선(Edge)
- 두 정점을 연결하는 연결선이다. 구체적으로는, 두 정점간의 관계이다.
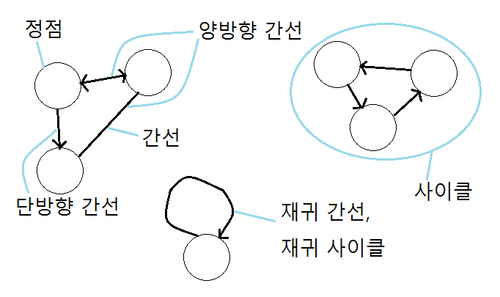
- 단방향 간선
- 단방향으로만 이동 가능한 간선이다. 이동이 가능한 방향으로 화살표를 그린다.
- 양방향 간선
- 양 방향으로 모두 이동이 가능한 간선이다. 양쪽 화살표를 사용해도 되지만, 양방향 그래프에서는 모든 간선이 양방향 간선이므로 화살표 대신 선분으로 표현하기도 한다.
- 자기 간선
- 자기 자신을 연결하는 간선이다.
- 다중 간선
- 동일한 다른 접점과 여러 간선이 연결되는 간선이다.
- 인접
- 두 정점이 하나의 간선으로 연결되어 있을 때 두 정점이 인접하다고 한다.
- 차수(Degree)
- 정점에 연결된 간선의 수이다.
- 진입 차수
- 정점으로 들어오는 간선의 수이다.
- 진출 차수
- 정점에서 나가는 간선의 수이다.
- 경로(Path)
- 어떤 한 정점에서 다른 하나의 정점으로 가는 길이다. 두 정점이 반드시 다를 필요는 없다.
- 길이(Length)
- 어떤 경로에서 시작 정점에서 도착 정점까지 거쳐야 하는 정점의 수.
- 단순 경로
- 경로에서 시작, 끝 정점을 제외한 방문하는 모든 점이 서로 다른 경로.
- 사이클(Cycle)
- 시작 정점과 끝 정점이 같은 단순 경로
- 재귀 사이클
- 간선 하나만으로 이루어진 사이클
- 부분 그래프(Sub Graph)
- 그래프를 구성하는 정점들을 임의로 선택한 후 그 정점을 연결했던 간선들로 선택한 정점을 연결한 그래프를 말한다.
그래프의 종류
- 그래프
- 일반적인 정의는 객체들 사이의 관계를 점과 선으로 나타낸 그림이다. 그래프는 크게 두 구성요소 정점과 간선으로 이루어져 있다.
- 단순 그래프
- 임의의 두 정점 사이에 간선이 최대 하나 있는 그래프
- 다중 그래프
- 임의의 두 정점 사이에 여러 개의 간선을 허용하는 그래프
- 의사 그래프
- 다중 그래프이면서 사이클을 허용하는 그래프
- 양방향(무향) 그래프
- 연결된 두 정점의 순서를 바꾸어도 같은 간선이 되는 그래프, 즉 양방향으로 통행이 가능한 그래프.
- 단방향(유향) 그래프
- 일방통행만 가능한 그래프.
- 연결 그래프
- 임의의 두 정점 사이에 반드시 경로가 존재하는 그래프.
- 완전 그래프
- 모든 정점이 서로 간선으로 양방향 연결되어 있는 그래프
- 가중치 그래프
- 간선에 가중치가 부여된 그래프
그래프 순회 알고리즘
그래프를 순회하는 방법이다. 각 방법마다 장단점이 있으니 상황에 따라 적절한 알고리즘을 선택하는 것이 중요하다.
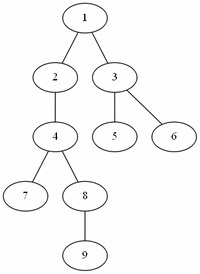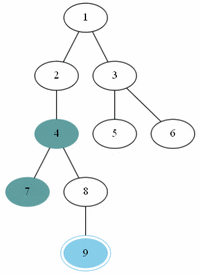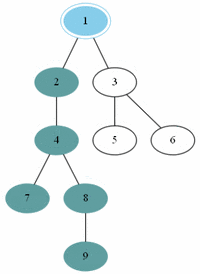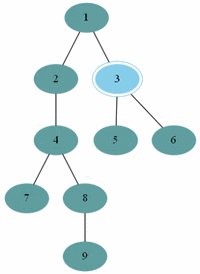
깊이 우선 탐색
Depth First Search, DFS라고 불리며, 구현하기 쉬운 알고리즘 중 하나이다. 이름 그대로, 방문한 정점으로부터 깊게 들어가며 쭉 탐색한 후, 되돌아 나오다가 아직 탐색하지 않은 노드를 탐색하는 방식을 사용한다.
알고리즘의 실행과정을 설명하면 다음과 같다.
- 첫 정점을 방문한다.
- 인접한 정점 중 아직 방문하지 않은 정점을 방문한다(한 길로 쭉 파고 들어간다).
- 더 이상 들어갈 길이 없을 때(인접한 모든 정점이 이미 방문한 정점일 때), 방문하지 않은 인접한 정점을 찾을 때까지 들어간 길을 돌아나온다.
- 위 과정을 반복한다.
여기서 DFS를 구현하는 함수의 모양은 다음과 같다. 단,그래프는 인접리스트를 활용했다고 가정한다.
bool visited[101]; //방문 여부를 체크하는 배열
void dfs(int k)
{
for(int i=0; i<G[i].size();i++) //정점 k와 연결된 모든 정점을 방문한다.
if(!visited[G[k][i].to])
{
visited[G[k][i].to]=true;
dfs(G[k][i]);
}
return;
}
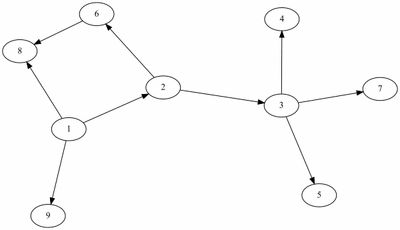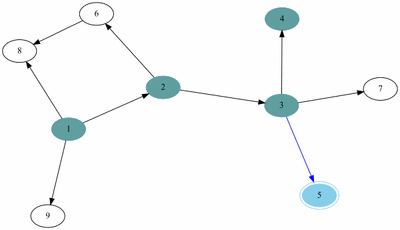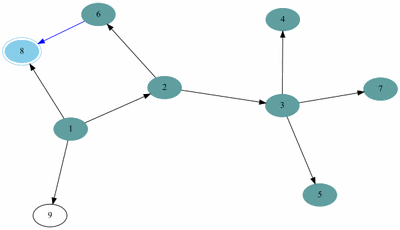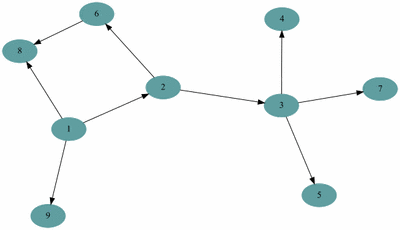
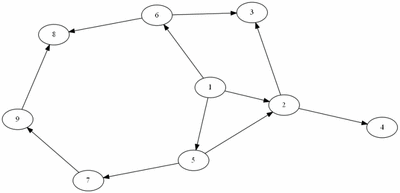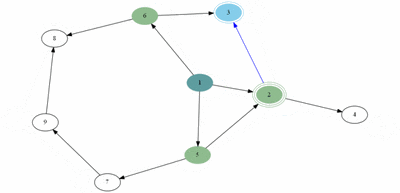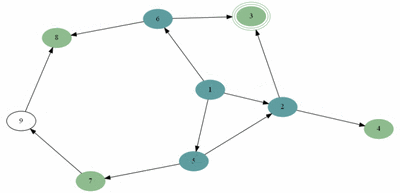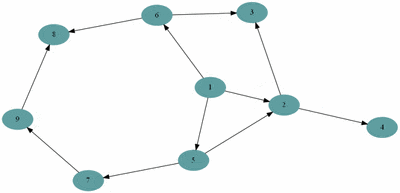
예제(그림)의 경우 방문 순서는 1, 2, 3, 4, 5, 7, 6, 8, 9 이다.
여기서 DFS는 깊이가 너무 큰 경우, 런타임 에러를 뿜는다는 단점이 있다.
너비 우선 탐색
Breadth First Search, BFS라고 불린다. 이름 그대로, 넓게 퍼져가며 정점을 방문한다.
알고리즘의 실행과정은 다음과 같다.
- 첫 정점을 방문한다.
- 아직 방문하지 않은 인접한 정점들을 큐에 넣는다.
- 큐에 있는 정점들을 순서대로 방문한다.
- 큐에 있는 정점에 대해 인접하면서 아직 방문하지 않은 정점들로 새로운 큐를 구성한다.
- 위 과정을 반복한다.
예제(그림)의 경우 방문 순서는 1, 2, 5, 6, 3, 4, 7, 8, 9 이다.
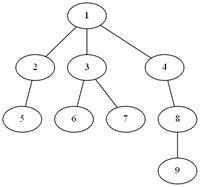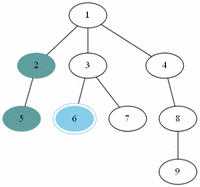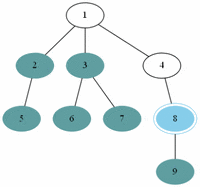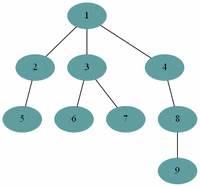
트리
그래프의 일종이다. 트리에서의 정점을 특별히 노드라고 하고, 간선을 특별히 가지라고 한다.
코드를 작성해보자.
struct Node;
struct List
{
struct List *next;
struct Node *element;
};
struct Node
{
struct Node *Parent;
struct List *Sons;
};
자식 노드의 수가 몇 개인지 모르기 때문에, 각 노드의 자식노드 리스트를 단방향 링크드 리스트를 이용해 저장하였다. 위의 struct Node가 하나 이상 있는 것이 트리이다.
트리 관련 용어
- 노드(Node)
- 그래프의 정점에 해당하는 것이다.
- 루트 노드
- 트리의 기준이 되는 노드이다. 나무의 뿌리를 생각하면 된다. 루트 노드 위에 가지가 뻗어 있다는 이미지.
- 부모 노드
- 어떤 노드에서 자신과 인접한 노드들 중 루트 노드로 향하는 노드.
- 자식 노드
- 어떤 노드에서 자신과 인접한 노드들 중 루트 노드의 반대 방향으로 향하는 노드.
- 단말 노드
- 자식 노드가 존재하지 않는 노드. 가지의 끝이라고 생각하면 된다.
- 형재 노드
- 부모 노드가 같은 노드.
- 가지(Branch)
- 그래프의 간선에 해당하는 것이다. 트리에서는 양방향 간선만 사용한다.
- 부트리(Sub Tree)
- 부분 그래프와 비슷하게 정의한다.
- 차수(Degree)
- 자식 노드의 개수.
- 길이(Length)
- 임의의 두 노드를 시작 노드, 도착 노드로 하는 경로에서 거치게 되는 노드의 수.
- 깊이(Depth)
- 루트 노드에서 해당 노드까지의 길이.
- 레벨(Level)
트리도 레벨업을 하나?- 깊이가 같은 노드의 집합.
- 높이(Height)
- 가장 깊이가 깊은 단말 노드까지의 길이.
트리의 종류
- 이진 트리
- 모든 노드의 차수가 2 이하인 트리.
- 전 이진 트리
- 모든 노드의 차수가 0 또는 2인 트리.
- 포화 이진 트리
- 모든 단말 노드의 깊이가 같은 이진 트리.
- 완전 이진 트리
- 모든 단말 노드의 깊이의 최댓값과 최솟값의 차이가 0 또는 1인 이진 트리.
트리 순회 알고리즘
트리를 순회하는 방법이다.
전위 순회
그래프에서의 깊이 우선 탐색과 같다. 설명은 해당 항목에서!
중위 순회
이진 트리에서만 할 수 있는 순회 알고리즘이다.
후위 순회
레벨 순서 순회
그래프에서의 너비 우선 탐색과 같다. 역시 설명은 해당 항목에서!
이진 검색 트리
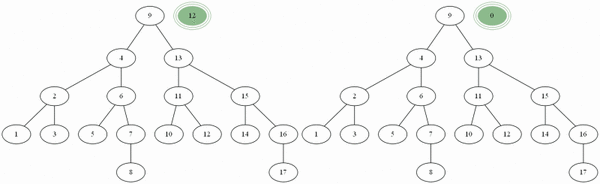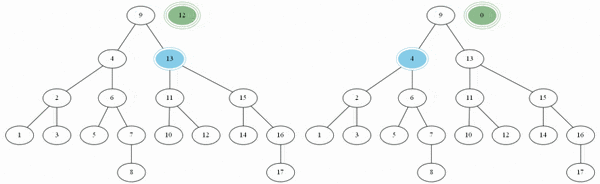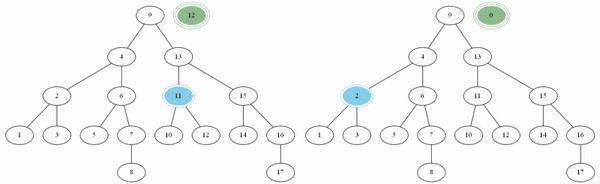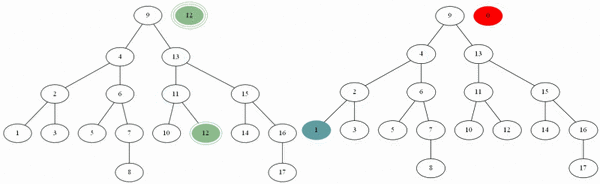
이진 검색은 일자로 나열된 정렬된 데이터에서 원하는 데이터를 빠르게 찾는 방법이다. 최악의 경우에 [math]\displaystyle{ O \left( \log{n} \right) }[/math]를 보장하는 매우 유용한 알고리즘이다. 정렬의 중요성은 거의 이 알고리즘을 통한 활용에 있다고 할 수 있다. 이진 검색 트리는 이진 검색에 용이하게 데이터를 다음과 같은 방법으로 이진트리로 구성한 것을 말한다.
- 일렬로 나열된 데이터들 중 가장 중앙에 위치한 하나의 데이터를 M이라고 하고, M 왼쪽에 위치한 데이터들을 L, 오른쪽에 위치한 데이터를 R이라 하자.
- L과 R이 M을 부모로 가지는 트리를 구성한다.
- L과 R에 대해서도 각각 같은 방법으로 트리를 구성한다.
이진 검색
이분 탐색과 동일한 알고리즘이다. 여기에서는 트리라는 특징을 중점으로 해서 설명한다. 오름차순 정렬된 자료를 기준으로 한다. 이진 검색 트리의 루트 노드부터 방문하며, 다음 순서에 따라 노드를 방문한다.
- 방문한 노드가 찾는 값이라면 검색 성공.
- 방문한 노드가 단말노드이고 찾는 값이 아니라면 검색 실패.
- 방문한 노드가 단말노드가 아니고 찾는 값이 아니라면
- 방문한 노드의 값을 [math]\displaystyle{ x }[/math], 찾는 값을 [math]\displaystyle{ v }[/math]라고 할 때, [math]\displaystyle{ x \lt v }[/math]
- 방문한 노드의 오른쪽 자식을 방문한다.
- [math]\displaystyle{ x \gt v }[/math]
- 방문한 노드의 왼쪽 자식을 방문한다.
- 방문한 노드의 값을 [math]\displaystyle{ x }[/math], 찾는 값을 [math]\displaystyle{ v }[/math]라고 할 때, [math]\displaystyle{ x \lt v }[/math]
여기서도 위에서와 같이 노드가 저장된 값에 특정한 규칙이 있어야 함에 주의해야 한다. (정렬이 가능한지는 추가바람)
문자열
문자 여러개가 나열되어 있는 것으로, 보통 배열로 표현한다. C에서, 문자열의 끝은 특정 문자(NULL, ASCII 0번 문자)로 정해져 있다. Java에서는 아예 기본 자료형으로 제공된다.
기초 정렬 알고리즘
정렬 알고리즘은 크기순, 사전순과 같이 정렬하는 알고리즘을 말한다. 효율적인 알고리즘들 중 대부분은 데이터가 사전에 정렬되어 있을 것을 요구하는 것이 많다. 또한, 정렬 알고리즘은 알고리즘의 기초 중의 기초이면서도 널리 쓰이는 알고리즘이다.
뿅뿅뿅뿅뿅 일단 이걸 보고 뭘 배우면 좋을지 생각해보자. 참고로 이걸 돌릴 수 있는 프로그램이 동영상에 적힌 웹사이트에 있다. 직접 속도조절을 해보면서 뭐가 빠른지, 어떻게 작동하는지 등등을 유심히 관찰하자. 근데 영어다. 참고로 소리를 직접 켜야 들을 수 있다.
영상을 보다보면 마지막의 보고(Bogo) 정렬은 결과를 보여주지 않는걸 보고 의아해 할 수도 있는데, 보고 정렬은 모든 값을 랜덤하게 줄세우는걸 반복하다보면 언젠가는 정렬이 된다는 식으로 동작하는 알고리즘이라서 그렇다(...) 알고리즘의 구성도 랜덤배치->정렬여부 확인의 무한루프. 당연하지만 효율성은 바닥을 긴다. 잘하면 한방에 정렬되지만, 영원히 정렬되지 않을 수도 있다. 기글 하드웨어의 한 유저가 10개의 값으로 테스트하니 결과를 보기까지 4천만번의 읽기작업이 수행되었다고 한다.[9]설마 이런데도 배우고 싶다고는 안하겠지?
거품(Bubble) 정렬
세상에서 가장 만만한 정렬(...) 어떤 사람은 선택 정렬이 더 쉬웠다 카더라 바로 뒤의 원소와 비교해 더 크다면 뒤로 간다. 구현이 쉬운 만큼 성능이 구리다. 알고리즘이 쉬워서 입문용으로 나오는 거지 사실 정렬이 되어 있든 아니든 대체적으로 느리고 캐시도 못 타고 여러모로 안 좋다. 공부할 목적으로만 쓰고 실제로 정렬을 돌려야한다면 쓰지 말자.
C언어 예제는 다음과 같다.
int arr[] = {5, 3, 7, 8, 6, 4, 2, 1, 0, 9};
void sort()
{
int i, j;
for(i = 0; i < 10; i++)
for(j = i; j < 9; j++)
if(arr[j] > arr[j + 1]) //j번째 원소가 다음 원소보다 크다면 바꾼다.
{
int temp;
temp = arr[j + 1];
arr[j+1] = arr[j];
arr[j] = temp;
}
}
파이썬으로 거품 정렬을 구현하는 예제 함수는 다음과 같다.
def bubbleSort(x):
length = len(x)-1
for i in range(length):
for j in range(length-i):
if x[j] > x[j+1]:
x[j], x[j+1] = x[j+1], x[j]
return x
선택(Selection) 정렬
거품정렬하고 살짝 다른 방식의 정렬이다. 구현 방식도 거품정렬하고 비슷하며 시간복잡도도 똑같이 O(n^2)이다. 그러나 한 가지 다른 점은 선택 정렬은 1번째부터 끝까지 훑어서 가장 작은 게 첫번째, 그 다음에 2번째부터 끝까지 훑어서 가장 작은 게 두번째, 그런 식으로 정렬하는 것이다. 역시 거품 정렬과 마찬가지로 공부용으로만 써보자.
C언어 예제 소스는 다음과 같다.
int arr[10]={4, 8, 6, 48, 64, 86, -4, -8, -6};
void sort()
{
int i,j,t;
for (i=0;i<9;i++)
for (j=i;j<10;j++) // 이 때 j는 무조건 i보다 크다
if (arr[i]>arr[j]) { // j번째(뒷) 원소가 i번째(앞) 원소보다 작을 때
t=arr[i];
arr[i]=arr[j];
arr[j]=t;
}
}
파이썬으로 선택 정렬을 구현하는 함수는 다음과 같다.
def selectionSort(x):
length = len(x)
for i in range(length-1):
for j in range(i+1, length):
if x[i] > x[j]:
x[i], x[j] = x[j], x[i]
return x
삽입(Insertion) 정렬
시간 복잡도 O(n^2)의 정렬 치고는 괜찮은 정렬이다. 이름 그대로 하나씩 삽입해 나가는 형태의 정렬방식으로, 특정 값에 대해서 그 값이 맞는 위치를 찾고, 나머지는 한칸씩 밀어낸다. 실제로 O(n2) 정렬 알고리즘 중에서는 가장 빠른 형태며, 대부분 정렬 알고리즘이 실행되는 시점이 정렬된 데이터에 새 값을 하나 넣을 때인데, 이 경우 삽입 정렬은 꽤 빠르다. 또, 값이 적은(10개 정도) 상태에서는 캐시도 잘 타기 때문에 여러 정렬 알고리즘에서도 적당히 큰 단위에선 퀵 소트를 쓰고 자잘한 단위에선 삽입 정렬을 쓰는 방식을 사용하기도 한다.
* 구현방법 1
int arr[10]={4, 8, 6, 48, 64, 86, -4, -8, -6};
void sort()
{
int i,j,t;
for (i=1;i<10;i++) {//i번째 값에 대해서
for (j=i-1;j>=0;j--) {//j를 i의 왼쪽으로 이동시켜가며
if (arr[j]>arr[j+1]) {//i번째 값이 커질 때까지 이동시킨다
t=arr[j];
arr[j]=arr[j+1];
arr[j+1]=t;
}
else break;//이동이 끝나면(제자리를 찾으면) 루프에서 나간다
}
}
}
파이썬으로 삽입정렬을 구현하는 함수는 다음과 같다.
def insertSort(x):
for i in range(1, len(x)):
j = i - 1
key = x[i]
while x[j] > key and j >= 0:
x[j+1] = x[j]
j = j - 1
x[j+1] = key
return x
다음 단계로
축하한다. 우리는 일단 밑바탕을 배운것이다. 이제 다음 단계로 넘어갈 차례이다. 이제부터 슬슬 긴장해야 한다.
각주
- ↑ 덧셈, 뺄셈, 비교, 대입 등의 기본적으로 더 이상 잘게 쪼갤 수 없는 연산의 갯수를 말한다.
- ↑ 정확히는, 대학교 수준의 수학을 사용하여 엄밀하게 정의하지만, 여기서는 생략하기로 하자. 너무 복잡하니깐!
- ↑ 물론, 상수 [math]\displaystyle{ C=100,000,000 }[/math] 수준으로 엄청나게 커지면 그 때는 문제가 되지만, 실제 프로그래밍에서 그런 상황은 발생하기 어렵다.
- ↑ [math]\displaystyle{ 3^n }[/math]도 O 표기법으로는 [math]\displaystyle{ 2^n }[/math]와 같다. 물론, [math]\displaystyle{ 150^n }[/math]라던지 [math]\displaystyle{ 14500^n }[/math]와 같은 시간 복잡도와도 같은 시간 복잡도를 나타내는 것이지만, 가장 간단한 형태인 [math]\displaystyle{ 2^n }[/math]로 나타내는 것.
- ↑ 상수가 다양할 수 있으므로 이의 범위를 넓게 잡았다.
- ↑ 컴퓨터과학에서는 로그 2를 상용로그로 쓴다.
- ↑ C++ STL의 그것보다 빠를 것이다. 다만 확장이 어려울 뿐.
- ↑ 사실 우리가 수학에서 잘만 써먹던 대로 ‘꼭짓점’과 ‘변’이라고 하면 된다. 그거랑 정확히 똑같은 개념이다. 그런데 이상하게 이 동네에서는 ‘정점’과 ‘간선’이라는 새로운 용어를 쓴다. 이래 놓고 “수학에서 말하는 그래프랑 다르다”는 식으로 생각하는 바보도 있으니 기가 막힐 노릇이다. 그래프 이론은 엄연히 수학의 일부이다.
- ↑ http://gigglehd.com/zbxe/10760945