잔글 (→다항함수의 미분법) |
|||
| 469번째 줄: | 469번째 줄: | ||
함수 <math>\definecolor{asd}{RGB}{255,0, 0} \color{asd}{{x}^{n}}</math>의 도함수는 다음과 같다.<ref>n은 실수이다.</ref><br> | 함수 <math>\definecolor{asd}{RGB}{255,0, 0} \color{asd}{{x}^{n}}</math>의 도함수는 다음과 같다.<ref>n은 실수이다.</ref><br> | ||
<math>\definecolor{asd}{RGB}{255,0, 0} \color{asd}{\frac{\mathrm d}{\mathrm dx}({x}^{n})=n{x}^{n-1}}</math> | |||
<math>\definecolor{asd}{RGB}{255,0, 0} \color{asd}{f(x)={x}^{n} \to f'(x)=n{x}^{n-1}}</math>. | |||
<math>\definecolor{asd}{RGB}{255,0, 0} \color{asd}{\frac{\mathrm d}{\mathrm dx}({x}^{n})=n{x}^{n-1}}</math> | |||
다음과 같은 계산 과정을 통해서 자연수에 대해서 증명이 가능하고, 미분에 대한 지식 몇 가지만 추가하면 실수 n에 대해서 확장할 수 있다. 그러나 어렵다 싶으면 일단 그냥 암기해서 이용해도 문제없는 부분이다. | 다음과 같은 계산 과정을 통해서 자연수에 대해서 증명이 가능하고, 미분에 대한 지식 몇 가지만 추가하면 실수 n에 대해서 확장할 수 있다. 그러나 어렵다 싶으면 일단 그냥 암기해서 이용해도 문제없는 부분이다. | ||
| 484번째 줄: | 487번째 줄: | ||
<math> \ln y = n \ln x</math> | <math> \ln y = n \ln x</math> | ||
양변을 미분하면 | 양변을 미분하면 | ||
| 492번째 줄: | 494번째 줄: | ||
<math> \frac{\mathrm dy}{\mathrm dx} = \frac{n}{x}y</math> | <math> \frac{\mathrm dy}{\mathrm dx} = \frac{n}{x}y</math> | ||
<math> y= x^n</math>이므로 이를 다시 위의 수식에 치환하면 | <math> y= x^n</math>이므로 이를 다시 위의 수식에 치환하면 | ||
2015년 5월 15일 (금) 15:46 판
들어가기 전
이 항목은 너 나 우리 수포자도 이해할 수 있는 수학 개념들을 적어보는 집단연구 문서이다.
수학 고수 여러분 부탁합니다
수학에서 중요하지만서도 우리 수포자들을 좌절케 하는 개념들을 위주로 서술하면 좋을 듯하다. 엄밀한 의미의 정의는 다른 문서에서 서술한다. 엄밀하게 들어가면 끝이 없기 때문에..
수학을 공부하는 이유
교과과정에서 흔히 만날 수 있는 수학은 이유도 목적도 알려주지 않은 채 일단 문제를 풀라는 식으로 되어 있는 경우가 많다.입시 교육의 폐해 애초에 수학은 왜 공부하는걸까?
수학 교과의 설명
수학과는 수학의 개념, 원리, 법칙을 이해하고 기능을 습득하여 주변의 여러 가지 현상을 수학적으로 관찰하고 해석하는 능력을 기르며, 수학적 문제 상황을 수리·논리적 사고를 통하여 합리적으로 해결하는 능력과 태도를 기르는 교과이다.[1]
원론적인 이야기... 이딴 얘기 때려치고!
수포자들에게 굳이 수학을 가르치는 이유
“ 사실 살면서 다시는 근의 공식을 쓰거나 미적분은 손도 댈 일이 없는 사람이 대부분이다. 그런데도 굳이 수학을 왜 가르칠까? 수학이 전체 교육과정의 일부인 것은 수학적 지식을 전수하기 위해서라기보다는 논리적 사고력을 키우기 위해서이다. “
라고들 보통 말한다.
만약 정말 저 말이 맞다면, 사실…… 수학 안가르쳐도 될 것 같다. 논리적 사고력은 퍼즐게임이랑 프로그래밍[2]으로 대부분 대체 가능하지 않을까? 결국 전국에 수학 교사가 정말 많기 때문에 수학을 정규교육 과정에서 제하면 전국에서 교사들이 들고 일어날 것이라는 현실적 장벽만 있다는 결론이 나고, 그들의 밥그릇 때문에 우리가 이 고생을 하고 있다(?)는 대단히 암울한 결론에 이른다.
하지만 정말 그럴까? (독자연구)[3]결론부터 말하면 그렇지 않다.
- 살면서 다시는 근의 공식을 쓰거나 미적분은 손도 댈 일이 없는 사람이 대부분인가?
- 이런 말을 하는 사람들은 치킨을 팔거나, 단순 사무직에 종사하거나 이런 이미지를 머릿속에 떠올리는 것인지 궁금하다.
- 정말 저렇게만 살 것이고 공부와는 담을 쌓고 살 거라면 모르겠으되, 당신이 공부를 한다면 수학은 계속 필요하다. 예를 들어 인문학과 사회학에도 수학적 모델과 과학적 방법론이 도입된지 오래다. 경제학은 물론이고 정치학을 하더라도 수학은 중요하다. 특히 통계학.
- 미분의 경우, 뭐든 수학적으로 모델링하면 미분방정식(아님 점화식)이 기본으로 튀어나온다.
- 행렬의 경우, 그 수학적 모델에서 변수가 두 개 이상만 되면 행렬이 튀어나온다.
- 지수와 로그의 경우는 미분방정식 풀면 기본으로 지수함수가 튀어나온다.
- 그것들을 ‘편하게’ 하라고 지금 미분을, 지금 행렬을, 지금 지수와 로그를 배우고 있는 것이다. 나중에 공부하다가 수학적 모델이 나왔을 때 개뼉다귀구만 하고 당연하게 생각할 수 있도록 지금 미리 사고방식을 연습해 두는 것이다.
- 나는 대학 안 가는데요? 대학 안 가면 평생 공부 안 하고 살 것 같은가? 공부는 평생 하는 것이다.
- 예를 들어 30대 40대 돼서 이직 자리 구할 일이 없을 것 같은가? 그때 대학 갓 졸업한 구직자들 그리고 다른 경력직 지원자들 사이에서 살아남기 위해 시험 하나라도 더 보고 자격증 하나라도 더 따려고 할 일이 없을 것 같은가? 그때 가서 그 시험과목 중에 수학적 기반을 필요로 하는 것이 있다면 본 척도 안 하고 그 자격증을 포기할 건가? 혹은 울며 겨자 먹기로 비싼 학원비 들여 가면서 내가 왜 학생 때 수학을 포기했을까 하고 한탄하고 있을 건가?
- 수학을 가르치는 이유는 논리적 사고력을 기르기 위해서인가?
- 일단 맞다. 그런데 ‘논리적 사고력’이라는 단어로는 다 전달이 안 되는 뭔가 더 엄청난 것이 있다. 수학적 사고의 기본은 ‘이 전제 하에서라면 답은 하나로 정해지는’ 경우 그 답이 뭔지 미리 알아 놓자는 것이다. 다만 그 답이 진짜 정답이도록 엄청 엄밀히 답을 구하고, 그리고 그렇게 답이 구해졌다면 부정하지 말자는 것이다.
- 답을 미리 알아 놓으면 좋은 일이 많다. 답을 미리 알아 놓으면, 답이 아닌 걸 붙들고 늘어지면서 발생하는 손해를 줄일 수 있다. 혹은 나쁜 답이 도출될 전제를 피해갈 수 있다. 아니 그게 답일지 아닐지 좋은 답일지 나쁜 답일지 어떻게 그렇게 확실하냐고? 그걸 확실하게 만들기 위해 논리적 사고를 배우는 것이다.
- 즉 논리적 사고력을 기른다는 추상적인 내용이 목표가 아니고, 당신이 확실하게 아닌 걸 맞다고 헛소리 지껄이는 거랑 확실하게 맞는 걸 아니라고 헛소리 지껄이는 상황을 막아서 당신이 세상을 좀 더 쉽고 편하게 살게 만드는 것이 목표이다. 즉 ‘당신이 확실하게 아닌 걸 맞다고 하지 않고 확실하게 맞는 걸 아니라고 하지 않는 논리적 사고력’을 기르는 것이 목표이다. 세상에 그렇게 확실한 게 있기는 있냐고?
- 예를 들어 사과 세 개가 있고 배 다섯 개가 있다. 총 몇 갠가? 8개이다. 승용차 석 대와 버스 다섯 대가 있다. 총 몇 댄가? 8대이다. 누가 왜 ‘8개/8대’야? 라고 물어보면 이렇게 대답할 것이다. “3+5=8이니까.” 여기다 대고 ‘7개’라거나 ‘9대’라고 우기는 사람은 없을 것이다. 왜? ‘세 개고 다섯 개인 이상 답은 8개로 정해졌기’ 때문이다. ‘석 대와 다섯 대인 이상 답은 8대로 정해졌기’ 때문이다. 세어 보면 누구든지 8개이고 8대임을 알 수 있고, 세어 보지 않고도, 눈 감고도 8개이고 8대임을 안다. 누가 7개임을 전제로 연구를 하거나 9대임을 전제로 강연을 하더라도, 냅두면 된다. 알아서 망할 것이다. 왜? 8개이고 8대니까. 8개이고 8대인 게 너무 당연해서 다른 생각을 안 하는가? 이미 당신은 수학적 사고에 발을 담그고 있는 것이다.
- 이번엔 좀 더 어려운 예를 들어 어떤 사람 甲이 길이가 3, 5, 7인 세 개의 철강 빔(beam)을 가지고 무슨 구조물을 만들려고 한다. 근데 사실 지금 목표가 구조물의 안정성을 위해서 예각삼각형을 만들어야 하는 거라고 하자. 수학 고수 乙이 이렇게 얘기한다. “길이가 3이랑 5인 빔이 만나는 쪽의 각도가 120˚가 돼서 불안정할 텐데?” 甲은 말한다. “야 임마 형 믿어. 내가 한두 번 해 보냐? 예각삼각형 되게 다 만드는 방법이 있어.” 어떻게 됐을까? 아까 표현대로 써 보면 이렇다. “누가 예각삼각형임을 전제로 구조물을 만들더라도, 냅두면 된다. 알아서 망할 것이다. 왜? 120˚니까.” 당연히 乙의 말대로 됐고, 甲은 빔 값을 날렸다(그리고 공사 기한을 못 맞추게 됐을지도 모르고, 채무불이행으로 손해배상책임을 졌을지도 모른다). 왜 그런가? ‘삼각형에서 세 변의 길이가 정해져 있다면 세 내각의 크기는 각각 하나로 정해지기’ 때문이다. 이 경우의 수학자들이 미리 알아 놓은 답이 바로 제2코사인법칙이다. 즉 식으로 쓰면 [math]\displaystyle{ c^2 = a^2 + b^2 - 2ab \cos C }[/math]. 지금 당장 c=7, a=3, b=5 넣고 cos C = −1/2가 나오는 점을 확인해 보아도 좋다. 甲처럼 직접 삼각형을 만들어 보면 누구든지 120˚임을 알 수 있고, 만들어 보지 않고도, 눈 감고도 120˚임을 안다. 아까 3+5=8이니까 8개이고 8대인 게 너무 당연해서 다른 생각을 안 했다면, 지금도 제2코사인법칙 때문에 120˚인 게 너무 당연해서 다른 생각을 하면 안 된다. 수학을 모르면 甲처럼 헛소리를 지껄이게 되고, 수학자들이 구해 놓은 답을 무시하면 甲처럼 망하게 된다.
- 이처럼 수학은 ‘이 전제 하에서라면 답은 하나로 정해지는’ 경우에 당신이 비껴가지 않게 해 준다. 그렇게 함으로써 당신의 시간과 노력과 비용을 절약하고, 당신이 세상을 좀 더 쉽고 편하게 살게 해 준다. 수학을 통해 거기 있는 게 황금인지, 용의 아가리인지 뻔히 알 수 있다. 그건 정해져 있다. 수학을 모르고 눈 앞의 황금을 놓치거나 용의 아가리로 돌진할 텐가, 아니면 지금 수학을 공부해 볼 텐가?
수학이 중요한 이유
굳이 인류 전체에게 수학을 가르쳐야 하는지는 모르겠지만 현대문명의 발달에 수학이 뗄 수 없는 존재인 것은 사실이다. 수학은 정말 쓰임새가 많은 학문이다. 수학의 쓸모를 설명하기 위해 많은 수포자들이 가장 눈꼴사납게 보는 것 중 하나인 미적분의 쓸모를 예로 들어보겠다.
미적분은 미세한 변화를 토대로 현실을 모델링하는 학문이다. 즉 방정식 몇개만 주면 현실을 상당히 정확히 시뮬레이션 할 수 있는 것이다. 덕분에 미적분은 현대 문명의 모든 곳에 다 쓰인다. 예를 들면:
- 날씨의 미세한 변화를 공부함으로써 지금의 날씨로 보아서 미래의 날씨를 예측할 수 있게 해준다.(나비에-스톡스 방정식)
- 전자기장의 미세한 변화를 공부함으로써 전자기장의 정확한 컨트롤을 할 수 있게 해준다. 이걸 열심히 한 덕분에 컴퓨터, 전구, 전자악기 등 모든 전자장비를 만들수 있게 되었다.(맥스웰 방정식)
- 화학반응의 미세한 변화를 공부함으로써 어떻게 화합물을 섞어야 최대효율로 섞을 수 있는지를 알게 되었고, 덕분에 샴푸나 칫솔, 비료 등의 제품들을 대량으로 얻을 수 있게 되었다.
- 금융경제의 미세한 변화를 공부함으로써 미래의 주식가격을 예측할 수 있게 해준다. (블랙-숄즈 방정식)
이 밖에도 정수론이나 상대성이론같은 자연의 신비를 연구하는 데에도 미적분이 사용된다.
한편 쓰임새를 다 떠나서, [math]\displaystyle{ \frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\cdots = \frac{\pi^2}6 }[/math]같은 식들을 보라. 제곱수의 역수들을 쭉 더했더니... 원의 둘레와 지름의 비율이 나왔다! 아무 관련 없는 두 개념이 신비롭게 연결되는 것을 목격할 수 있다. (그리고 이걸 증명하는 것도 쉽지는 않다) 수학공부를 깊게 하면 이런 경이로움을 밥먹듯이 만나기 때문에 재미로만 수학연구를 계속 하는 수학자들이 존재한다.
정수론
사실 많은 내용이 나오지 않는다. 이 뒤의 심화 내용들이 문제지만..
나머지 정리
모든 정수는 다른 정수로 나눈 몫과 나머지를 이용해 나타낼 수 있다. 그런데 그렇게 나타내는 방법은 제수(다른 수를 나누는 수)가 정해지면 유일하다는 것이다.
- 몫과 나머지에 대한 설명 추가바람
예를 들어, 7을 3으로 나눈다고 하자. 그러면 몫은 2, 나머지는 1이다. 따라서, [math]\displaystyle{ 7=3\times 2+1 }[/math]이라고 쓸 수 있다. 그런데 7을 3으로 나눌 때 몫은 2 이외의 값이 안 나오고 나머지도 1 이외의 값이 안 나온다.
이번에는 -12를 5로 나눈다고 하자. 그러면 몫은 -3, 나머지는 3이다. 따라서, [math]\displaystyle{ -12=5\times \left(-3\right)+3 }[/math]이라고 쓸 수 있다. 여기에서 중요한 것은 제수는 항상 자연수이고, 나머지는 0 이상이며 제수보다 작은 정수이다. 나머지를 이렇게 정의하면, 앞서 제시한 예와 마찬가지로 -12를 5으로 나눌 때 몫은 -3 이외의 값이 안 나오고 나머지도 3 이외의 값이 안 나온다.
- F[t]의 나머지 정리와 인수정리에 대한 내용 추가바람
나누어 떨어짐
위의 나머지 정리에서 나머지가 0인 경우이다.
예를 들어, [math]\displaystyle{ -15=5\times -3 }[/math]에서 나머지는 0이 된다. 이 때, -15는 5로 나누어 떨어진다고 한다. -15는 5의 배수이고, 5는 -15의 약수이다.
소수
1과 자신만을 약수로 갖는 자연수이다. 잘 알고 있듯이, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, ... 이렇게 계속 나아간다.
소수 판정법
어떤 자연수가 소수인지 판별하는 방법이다. 방법은 여러가지가 있다.
에라토스테네스의 체
[math]\displaystyle{ n }[/math]이 소인수 [math]\displaystyle{ p \lt n }[/math]을 가지면 [math]\displaystyle{ p \leq \sqrt{n} }[/math]임을 이용한 방법
이게 대체 무슨 소리야
이전에 [math]\displaystyle{ n=p\times q\left(p\le q\right) }[/math]일 때 [math]\displaystyle{ p\le\sqrt{n} }[/math]라고 쓰여 있었는데, n에 소인수가 둘뿐이란 보장이 어디 있는가? n이 소수가 아니어서 소인수 p<n을 가질 때 그 p의 성질이지, n=pq일 때에 대한 얘기가 아니다. 착각하면 곤란하다.
매번 판정할 때마다 에라토스테네스의 체를 사용하면 정말 많은 시간과 공간이 필요하다. 그걸 획기적으로 줄여주는게 이 방법이다. 2부터 [math]\displaystyle{ \sqrt{n} }[/math]까지의 소수로 [math]\displaystyle{ n }[/math]을 나눠보기만 하면 된다는 뜻이다.
이걸 증명하려면 약간의 증명이 필요하다. 증명 과정에서 각 가정들과 그 가정을 통해 이끌어지는 결과들을 주의깊게 살펴보기 바란다. 사실 한 번 보면 다시는 안 봐도 된다
수식 주의
임의의 자연수 [math]\displaystyle{ n }[/math]은 1이 아닌 이상 무조건 2 이상의 소수로 나누어 떨어진다. 이는 위의 에라토스테네스의 체를 사용하면 알 수 있다. 따라서, [math]\displaystyle{ n }[/math]를 나누는 가장 작은 소수를 [math]\displaystyle{ p_0 }[/math]라고 하면 [math]\displaystyle{ 2\le p_0 \le \frac{n}{2} }[/math]를 만족하게 된다. [math]\displaystyle{ 2 \le p_0 \le p_1 \le \cdots \le p_m \lt n }[/math]([math]\displaystyle{ p_0,p_1,\cdots,p_m }[/math]은 자연수)라고 하면 [math]\displaystyle{ n=p_0\times\frac{n}{p_0}=p_1\times\frac{n}{p_1}=\cdots=p_m\times\frac{n}{p_m} }[/math]이 된다. 여기에서 빠르고 편한 판정을 위해 [math]\displaystyle{ p_0 \le\frac{n}{p_0},p_1 \le\frac{n}{p_1},\cdots,p_m \le\frac{n}{p_m} }[/math]라고 해두자. 그러면 [math]\displaystyle{ p_0 \le p_1 \le \cdots \le p_m \le k \le \le\frac{n}{p_m}\le\frac{n}{p_{m-1}}\le\cdots\le\frac{n}{p_0} }[/math]을 만족하는 k가 반드시 존재하게 된다. 만약 [math]\displaystyle{ p_m=\frac{n}{p_m}=k }[/math]가 만족된다면, [math]\displaystyle{ k=\sqrt{n} }[/math]를 얻을 수 있다. 그러면 [math]\displaystyle{ p_0 \le p_1 \le \cdots \le p_m \le \sqrt{n} }[/math]로 결론을 얻는다.
소인수 분해
정수 함수
절댓값
절댓값의 정의는 어떤 수를 수직선에 표시했을 때 원점(0)에서부터의 거리인데, 그냥 부호만 빼면 된다. 4의 절대값은 4이고 -3의 절댓값은 3이 된다.
기하학
유클리드 기하
도형의 대칭
도형의 합동
도형의 닮음
닮음의 조건은
- (SSS 조건) 세 쌍의 대응변의 길이의 비가 같다.
- (SAS 조건) 두 쌍의 대응변의 길이 비가 같고, 그 끼인각의 크기가 같다.
- (AA 조건) 두 쌍의 대응각의 크기가 같다.
학교에서는 이 세 조건중 하나만 만족하면 두 삼각형이 닮음이라고 하고 기호로 ∽ 또는 ~를 사용한다. 기호의 유래는 여기를 참고하시길. 그런데 왜 별로 쓸모없어 보이는 닮음을 배우느냐... 직각삼각형때문에 그렇다. 직각삼각형은 결국 한 각만 같으면 나머지 하나가 직각이므로 서로 모두 닮은 삼각형이기 때문이다. 직각삼각형의 한 각만 알 수 있다면, 각 변마다 비율이 일정해져 버린다. 이제 본격적인 삼각함수 공부에 예열을 거는 것이다.
삼각형
피타고라스 정리
피타고라스의 정리는 초딩도 알고 있을만큼 상당히 단순한 정리이다.
이 정리를 통해서 무리수의 존재를 대략이나마 유추할 수 있다. 예를 들어, 양변의 길이가 1인 직각삼각형이 있으면, 피타고라스의 정리에 의해 나머지 빗변의 길이가 제곱하면 2가 되는 숫자가 나와야 하는데, 이 숫자가 자연수 중에서도 존재하지 않고, 유리수 중에서도 존재하지 않는다는 사실을 깨달을 수 있다는 것. 이 [math]\displaystyle{ \sqrt 2 }[/math]가 무리수임을 보이는 증명은 귀류법의 대표적인 문항으로 수포자가 아니라면 아예 외워 두는 사람도 많으나, 수포자라면 일단은 보기만 하자. 귀류법 자체가 처음에는 상당히 난해하다.
증명: [math]\displaystyle{ \sqrt 2 }[/math]가 유리수라면 [math]\displaystyle{ \sqrt 2= \frac a b }[/math] ([math]\displaystyle{ b \neq 0 }[/math], [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math]는 서로 소인 정수, 즉 기약분수)꼴로 둘 수 있다.
따라서, [math]\displaystyle{ \sqrt 2 }[/math]는 위와 같은 기약분수꼴로 나타낼 수 없고, 유리수가 아니다.
양변을 제곱하면 [math]\displaystyle{ 2=\frac {a^2} {b^2} }[/math]
양변에 [math]\displaystyle{ b^2 }[/math]을 곱하면 [math]\displaystyle{ 2 b^2=a^2 }[/math]
[math]\displaystyle{ 2 b^2 }[/math]이 2의 배수, 즉 짝수이므로 [math]\displaystyle{ a^2 }[/math]도 짝수이다.
제곱해서 짝수가 나오는 수는 짝수 뿐이므로(홀수의 제곱은 홀수), [math]\displaystyle{ a }[/math]는 짝수이고 [math]\displaystyle{ a=2k }[/math] ([math]\displaystyle{ k }[/math]는 정수)로 바꿀 수 있다.
[math]\displaystyle{ a=2k }[/math]를 [math]\displaystyle{ 2 b^2=a^2 }[/math]에 대입해 정리하면 [math]\displaystyle{ b^2=2k^2 }[/math]
같은 방법으로 [math]\displaystyle{ b }[/math]는 2의 배수이므로 짝수이다.
[math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math] 모두 짝수이므로(어????), 모두 2로 나눌 수 있으니 모순이다.
훨씬 더 쉬운 증명은 아래와 같다(여전히 귀류법이긴 하다).
증명: [math]\displaystyle{ \sqrt 2 }[/math]가 유리수라면 적당한 정수 [math]\displaystyle{ a }[/math]와 [math]\displaystyle{ b \neq 0 }[/math]에 대해 [math]\displaystyle{ \sqrt 2= \frac a b }[/math]로 둘 수 있다(기약분수가 아니어도 아무런 상관이 없다!).
[math]\displaystyle{ \sqrt 2 }[/math]가 유리수라고 가정하니 모순이 생겼으므로, [math]\displaystyle{ \sqrt 2 }[/math]는 유리수가 아니고 무리수이다.
양변을 제곱하여 정리하면 [math]\displaystyle{ a^2=2 b^2 }[/math]을 얻는다.
이제 양변의 소인수분해를 생각하면, 좌변에는 2가 짝수 개 있고, 우변에는 2가 홀수 개 있다. 따라서 모순이다.
(왜냐면 예를 들어 [math]\displaystyle{ a }[/math]의 소인수분해에 2가 3개 있다고 하면 [math]\displaystyle{ a^2 }[/math]의 소인수분해에는 2가 6개 있어야 하기 때문이다. [math]\displaystyle{ b }[/math]도 마찬가지.)
이 증명 자체를 이해하는게 어려울지라도, 최소한 [math]\displaystyle{ \sqrt 2 }[/math]는 유리수가 아님을 명심하자.
그리스의 피타고라스 학파 중 한 사람인 히파수스란 자가 빗변의 길이가 자연수 꼴로 나타나지 않는 경우도 있음을 알아차렸고, 또 이를 학파 밖의 다른 사람에게 이야기를 해서 죽임을 당했다고는 하는데, 정확한 사실은 아닌듯 하니 확인은 불가!
또, 바로 밑에 있는 해석 기하에 유용하게 써 먹을라고 배우는 것이다. 우리가 좌표 평면에서 두 점 사이의 거리를 계산할 때 피타고라스의 정리를 사용해서 구하고 있다(고 교과서에도 나온다). 이게 가장 중요한 이유이다.
사인 법칙
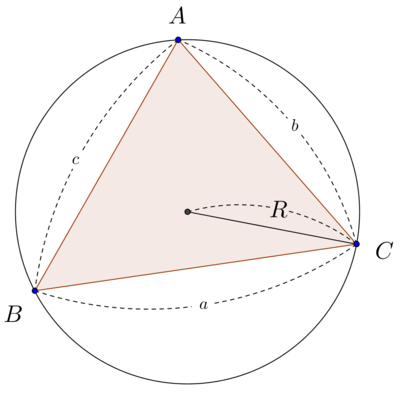
삼각형 ABC에 대하여 외접원의 반지름을 R이라 할 때, [math]\displaystyle{ \frac{a} {\sin A} =\frac{b} {\sin B}=\frac{c} {\sin C}=2R }[/math]가 성립한다. 사인 법칙은 두 각과 마주보는 변의 크기에 대해 알려졌을 때 사용하면 좋다. 예를 들자면 삼각형에 대해 A와 B의 크기, b의 길이를 주고 a의 길이를 구할때, 혹은 A의 크기와 a와 b의 길이가 주어졌을때, B의 크기를 구할때 사용하면 된다. 혹은 삼각형의 외접원의 길이 R과 A의 크기가 주어졌을때 a의 길이를 구할때, 혹은 외접원의 길이 R과 a의 길이가 주어졌을때 A의 크기를 구할때 사용하면 된다.
사인법칙을 물리학적으로 접근하면 라미의 정리가 된다.
코사인 법칙
삼각형의 세 변에 대하여 [math]\displaystyle{ a^2 = b^2 + c^2 - 2bc \cos A }[/math]가 성립한다. 코사인 법칙은 두 변과 끼인 각의 크기가 주어지고 끼인 각에 대한 마주보는 변의 길이를 구할 때 사용한다. 암기할 때는 abc cbA 이런 식으로 외우면 좋다.
식을 변형 시키면 [math]\displaystyle{ \cos A=\frac{b^2 + c^2 - a^2}{2bc} }[/math]가 되는데 이 형태는 세 변의 길이가 주어졌을 때, 어느 각에 대한 크기를 구할때 사용한다.
원
해석 기하
해석 기하의 유용함을 들 때 사용하는 설명은 중선 정리(또는 아폴로니우스의 정리, 파푸스의 중선 정리라는 이름은 우리나라하고 일본만 쓴다 카더라)를 예로 많이 든다.
좌표로 돌리고 풀면 쉽게 증명할 수 있다.
정리) [math]\displaystyle{ \operatorname{\overline {AB}^2+\overline {AC}^2=2(\overline {AM}^2+\overline {BM}^2)} }[/math]
증명) [math]\displaystyle{ \operatorname{\overline {AB}^2+\overline {AC}^2}= \{ (a+c)^2+b^2 \} + \{ (a-c)^2+b^2 \} =2a^2+2b^2+2c^2 }[/math] [math]\displaystyle{ 2a^2+2b^2+2c^2=2\{(a^2 + b^2) + c^2 \}=\operatorname{2(\overline {AM}^2+\overline {BM}^2)} }[/math]
그런데 왜 타원 방정식, 쌍곡선 방정식 이런 어려운 걸 푸냐고?? 쉽게 풀 수 있으니까 이제 어려운거 도전해야지!! 조삼모사???
방정식과 부등식
방정식
방정식이란 등식의 일종으로 x에 어떤 값을 대입하느냐에 따라서 식의 참과 거짓이 바뀌는 식을 의미한다. 예를 들어
[math]\displaystyle{ 2x+1=3 }[/math]
이라는 식이 있다고 하자. 위 식에 [math]\displaystyle{ x=0 }[/math]을 넣으면 [math]\displaystyle{ 2(0)+1=1\neq3 }[/math]여서 거짓이 되지만, [math]\displaystyle{ x=1 }[/math]을 넣으면 [math]\displaystyle{ 2(1)+1=3 }[/math]이여서 등식이 참이 됨을 쉽게 알 수 있다. 이 때, 이렇게 방정식을 만족시키도록 하는 x값을 우리는 방정식의 근 또는 해라고 하며 이러한 근을 구하는 것이 방정식의 일반적인 목표가 된다.
[math]\displaystyle{ ax+b=0 }[/math]꼴의 방정식
이항하여 [math]\displaystyle{ ax=-b }[/math]의 형태로 정리한다.
- [math]\displaystyle{ a=0, b=0 }[/math]일 때, 해가 무수히 많다.(부정=너무 많아서 정할 수 없다.)
- [math]\displaystyle{ a=0, b\neq0 }[/math]일 때, 해가 없다.(불능=해를 찾는 것이 불가능하다.)
- [math]\displaystyle{ a\neq0 }[/math]일 때, 아래 일차방정식 참고
일차방정식
최고 차수가 1인 방정식, 즉 [math]\displaystyle{ ax+b=0 }[/math] 꼴로 만들 수 있는 방정식이다. 일차라고 했으므로 이렇게 적을 때는 [math]\displaystyle{ a \neq 0 }[/math]이다.
이항하여 [math]\displaystyle{ ax=-b }[/math] 형태로 정리한 후 양변을 [math]\displaystyle{ a }[/math]로 나누면 해가 나온다.
[math]\displaystyle{ (x =-{ b \over a}) }[/math]
즉, 일차방정식 문제가 나오면 기본적으로 x에 대해서, 정리해 보고 생각해 보는 것이 좋다.
이걸 어디에 어디다 쓰는가? 실생활에 엄청, 진짜 엄청 많다. 이차방정식과는 비교를 불허한다. 근데 푸는 방법 보면 알겠지만, 방정식 안 세우고 그냥 곱셈 나눗셈으로 해결해 버릴 수도 있어서……
예시 추가바람
예제) [math]\displaystyle{ (a^2-1)x=a-1 }[/math]의 해가 무수히 많도록 하는 [math]\displaystyle{ a }[/math]를 구하시오. sol) 일단 인수분해가 안 되어 있으면, 인수분해부터 하고 보자.
인수분해를 하면 식이 [math]\displaystyle{ (a-1)(a+1)x=(a-1) }[/math]이 된다.
일차방정식의 해가 무수히 많은 경우는 [math]\displaystyle{ 0\times x=0 }[/math]을 꼴을 만족하는 경우였으므로,
[math]\displaystyle{ (a-1)(a+1) }[/math]과 [math]\displaystyle{ (a-1) }[/math]을 모두 0으로 만드는 값인 1이 답이된다.
연립일차방정식
이차방정식
이차방정식이란 최고차항이 2차항인 방정식, 즉 [math]\displaystyle{ ax^2 + bx + c = 0 }[/math] 꼴의 방정식을 말한다. 최고차항이 2차항이므로, 당연히 [math]\displaystyle{ a \neq 0 }[/math]임을 함의한다.
이차방정식의 풀이 전략은 보통 다음과 같다.
- 인수분해를 한다.
- 근의 공식 [math]\displaystyle{ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} }[/math]를 이용한다.
즉 인수분해를 할 수 없거나, (할 수 있더라도) 어떻게 해야 할지 모르겠는 경우에는 근의 공식을 써야만 한다. 그리고 근의 공식을 쓰면 언제나 풀린다.
근의 공식을 못 외우겠어요! 그 경우 근의 공식을 유도하는 아래 방법을 따라가면 된다. 괜히 유도방법을 주저리주저리 적어 놓은 게 아니다. 사실 생각해 보면 이차방정식을 풀기 위한 굉장히 당연한 방식이고, 이 유도방법을 따라가다 보면 근의 공식이 저절로 외워질 수도 있다.
사실 요즘 계산기가 잘 돼 있어서, 위 [math]\displaystyle{ ax^2 + bx + c = 0 }[/math] 꼴에 해당하는 a, b, c의 값만 차례로 입력하면 알아서 해를 구해 주기는 한다. 3차, 4차 방정식도 마찬가지.
제곱근의 성질무리수 파트로 옮기는게 나을 것 같습니다.
- [math]\displaystyle{ \sqrt{a} \times \sqrt{b} = \sqrt{ab} }[/math]
- [math]\displaystyle{ \sqrt{a} + \sqrt{b} \neq \sqrt{a+b} }[/math]이다. 예시를 들면 [math]\displaystyle{ \sqrt 9 + \sqrt 4 = \sqrt 25 \neq \sqrt 13 }[/math]이다.
- [math]\displaystyle{ \sqrt{a} \div \sqrt{b} = \sqrt{a \over b} }[/math]
- [math]\displaystyle{ \sqrt{a^2 \times b} = a\sqrt{b} }[/math]
- [math]\displaystyle{ a^2=b }[/math]일때 [math]\displaystyle{ a=\pm\sqrt{b} }[/math]이다.
이건 기본 상식이니 외워두자.
인수분해가 무엇인가?
인수분해(factorization)이란, 어떤 다항식을 그 식의 인수들의 곱으로 나타내는 것을 말한다. 인수란 그 다항식을 나누는 다른 다항식이다.
예를 들어 우리는 자연수 12를 [math]\displaystyle{ 12=2^2\times 3 }[/math]으로 소인수분해할 수 있음을 알고 있다. 여기서의 인수가 바로 그 인수이다.
이는 문자가 포함되어 있는 식에도 동일하게 적용될 수 있다. 만약에 [math]\displaystyle{ (a+b)^2 }[/math]라는 식이 있다고 하자. 이를 전개하면 [math]\displaystyle{ a^2+2ab+b^2 }[/math]이 된다.
즉,
[math]\displaystyle{ a^2+2ab+b^2=(a+b)^2 }[/math]
이다. 여기서 [math]\displaystyle{ a^2+2ab+b^2 }[/math]를 [math]\displaystyle{ (a+b)\times(a+b) }[/math]의 곱하기의 형태로 표현 했으므로, 이것이 바로 인수분해이다. 즉, 인순분해와 전개는 서로 거꾸로라고 할 수 있다.
인수분해는 고등학교 1학년 때 배우는 부분이지만 그 이후 3학년까지 계속해서 사용되므로 전부 능숙하게 할 수 있어야 한다. 그리고 물론 능숙하게 하기 위해서는 많은 연습을 통해 요령을 아는 것이 중요하다.
인수분해 공식
- [math]\displaystyle{ a^2 \pm 2ab+b^2=(a \pm b)^2 }[/math]
- [math]\displaystyle{ a^2-b^2=(a+b)(a-b) }[/math]
- [math]\displaystyle{ x^2+(a+b)x+ab=(x+a)(x+b) }[/math]
- [math]\displaystyle{ acx^2+(ad+bc)x+bd=(ax+b)(cx+d) }[/math]
이 외에도 많이 있으나 일단 이차식에 사용되는 공식은 이 정도 이다.
이차방정식의 근의 공식의 유도
일단 기본 아이디어는 “완전제곱식으로 만들자”는 것이다. 즉, [math]\displaystyle{ y^2 = k }[/math]라면 [math]\displaystyle{ y = \pm \sqrt{k} }[/math]임을 이용하자는 것이다. 아래에서 어떻게 완전제곱식을 만드는지 감상해 보자.
1. 무엇보다 먼저 이차방정식을 [math]\displaystyle{ ax^2+bx+c=0 }[/math] 꼴로 정리한다(별 소리 아닌 것 같지만 중요하다).
2. [math]\displaystyle{ \Leftrightarrow x^2+\frac{b}{a}x+\frac{c}{a}=0 }[/math] (양변을 [math]\displaystyle{ a }[/math]로 나눔)
3. [math]\displaystyle{ \Leftrightarrow x^2+\frac{b}{a}x=-\frac{c}{a} }[/math] (상수항을 우변으로 이항)
4. [math]\displaystyle{ \Leftrightarrow x^2+\frac{b}{a}x+(\frac{b}{2a})^2=(\frac{b}{2a})^2-\frac{c}{a} }[/math] (★★★★★)
5. [math]\displaystyle{ \Leftrightarrow (x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2} }[/math] (좌변은 인수분해, 우변은 통분)
6. [math]\displaystyle{ \Leftrightarrow x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a} }[/math] (완전제곱식 꼴의 이차방정식의 풀이)
7. [math]\displaystyle{ \Leftrightarrow x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} }[/math] (상수항을 우변으로 몰아서 정리하면 끝!)
위 별표 5개 쳐진 4단계가 제일 중요하다!! 저 단계만 제대로 할 줄 알면 근의 공식을 다 이해한 거나 마찬가지이다.
지금 좌변을 완전제곱식 꼴, 즉 [math]\displaystyle{ (x+q)^2 }[/math]가 전개된 형태([math]\displaystyle{ x^2+2qx+q^2 }[/math])로 만드는 것이 목적이다. 그러기 위해서는
- ‘일차항의 계수 [math]\displaystyle{ \tfrac{b}{a} }[/math]의 절반의 제곱’
을 좌우변에 더해야 한다. 이렇게 하면 좌변은 완전제곱식, 우변은 상수! 가 되어 이차방정식을 풀 모든 준비가 끝난 것이다.
아니, 인수분해 공식에 [math]\displaystyle{ (px+q)^2 }[/math]도 있는데 [math]\displaystyle{ p^2x^2+2pqx+q^2 }[/math] 꼴로 만들면 안 되냐고? 물론 된다. 그때는 ‘일차항의 계수 [math]\displaystyle{ \tfrac{b}{a} }[/math]의 절반의 제곱의 [math]\displaystyle{ a }[/math]배’(헥헥)를 더하면 된다. 근데…… 헷갈린다. 무엇보다 귀찮다. 그래서 처음에 양변을 [math]\displaystyle{ a }[/math]로 나누고 시작한 것이다. 즉 어렵게 만들려고 유도과정을 이렇게저렇게 꼬아 놓은 게 아니고, 제일 생각하기 편한 방식으로 하고 있는 것이다.
실제로 이차방정식을 하나 풀어 보면 훨씬 감이 잘 올 것이다.
문제) 다음 이차방정식의 해를 구하시오. [math]\displaystyle{ x^2 - x - 1 = 0 }[/math]
풀이)일단 인수분해가 안 된다! 완전제곱식 꼴로 만들 생각을 해 본다.
우선 상수항이 걸리적거리니까 우변으로 옮긴다. [math]\displaystyle{ \Leftrightarrow x^2 - x = 1 }[/math]
좌변에 뭘 더해 줘야 완전제곱식 꼴이 될지 고민한다. 답은 일차항의 계수의 절반의 제곱. 즉, 1/4이다.
즉 [math]\displaystyle{ \Leftrightarrow x^2 - x + \tfrac{1}{4} = \tfrac{5}{4} \Leftrightarrow (x-\tfrac{1}{2})^2 = \tfrac{5}{4} }[/math].이런 꼴의 이차방정식은 풀 수 있다!
즉, [math]\displaystyle{ \Leftrightarrow x - \tfrac{1}{2} = \pm \tfrac{\sqrt{5}}{2} \Leftrightarrow x = \tfrac{1 \pm \sqrt{5}}{2} }[/math]. 끝!
위 과정을 일반적인 경우에 대하여 문자로 나타낸 것이 근의 공식일 뿐이다. 즉 어려울 것이 하나도 없다.
참고로 지금 황금비(golden ratio)를 구한 것이다(정확히는 [math]\displaystyle{ \tfrac{1 + \sqrt{5}}{2} = 1.618 \cdots }[/math]가 황금비).
부등식
부등식이란, 부등호가 포함되어 있는 식을 의미한다. 우리가 지금까지 보아왔던 방정식에서 단지 등호가 부등호로 바뀌었을 뿐 큰 차이는 없다. 다만 몇 가지 중요한 내용은 확실하게 기억하자.
부등식의 성질
[math]\displaystyle{ a\lt b }[/math]이라고 할 때,
- [math]\displaystyle{ a+c\lt b+c }[/math]
- [math]\displaystyle{ a-c\lt b-c }[/math]
- [math]\displaystyle{ \begin{cases} ac\lt bc, &\mbox{if }c\gt 0\\ ac\gt bc, &\mbox{if }c\lt 0 \end{cases} }[/math]
- [math]\displaystyle{ \begin{cases} \tfrac{a}{c}\lt \tfrac{b}{c}, &\mbox{if }c\gt 0\\ \tfrac{a}{c}\gt \tfrac{b}{c}, &\mbox{if }c\lt 0 \end{cases} }[/math]
중요한 것은 곱하기와 나누기이다. 꼭! 기억하자. 부등식은 음수를 곱하거나 음수로 나누면 부등호의 방향이 바뀐다!
일차부등식
어디다 쓰는가? 실생활에 진짜 어어어어어어엄청 많다. 일차방정식보다 훨씬 더 많다!
- 감자를 사러 3천 원을 갖고 나왔는데 100g에 150원이다(참고로 엄청 싼 거다). 몇 그램 살 수 있을까?
- 학생들 484명을 강당에 앉혀야 하는데 한 줄에 20명씩 앉도록 의자를 배치하려고 한다. 최소 몇 줄 깔아야 할까?
- “어 지금 열심히 밟고 있어 2시까지 도착하면 되는 거지? 유성 톨게이트에서 들어가는 데 지금 길 안 막히니까 15분이면 넉넉하지 않나? 나 이제 막 (서울) 톨게이트 지났는데 한번 시간 안에 가 볼게. 뭐? 지금이 1시 5분 전인데 평균 시속 몇 킬로미터로 밟아야 하냐구?”
이차부등식
함수(해석학)
위에서 배운 방정식을 떠올려 보자. 예를들어
[math]\displaystyle{ 2x+1=3 }[/math]
라는 식이 있다면, 이 식을 만족하는 x는 유일하게 3으로 정해지며 이를 방정식의 근이라고 부른다.
함수는 이러한 방적식에서 확장된 것이다. 이제 다음과 같은 식을 생각해 보자.
[math]\displaystyle{ 2x+1=y }[/math](보통은 y를 왼편에 둬서 [math]\displaystyle{ y=2x+1 }[/math]의 형태로 쓴다.)
이 식은 x와 y의 두 개의 문자로 이루어져 있다. 여기서 만약에 x에 1을 대입하면 y=3 단 하나로 결정이 되고, x=2를 대입하면 역시 y=5로 유일하게 결정이 된다. 이렇게 x값에 따라서 y값이 유일하게 결정되는 관계를 우리는 함수라고 부르며 x를 독립변수, y를 종속변수라고 부른다.
방정식의 근이 하나 또는 여러 개의 x값으로 나타난다면, 함수를 만족하는 (x,y) 순서쌍은 무수히 많이 존재할 것이다. 이러한 (x,y)들을 좌표평면상에 그림으로 나타낸 것이 바로 함수의 그래프이다. 즉, 방정식->근, 함수->그래프라고 생각하면 된다.
사실 예전에는 집합 개념으로 도입했지만 이걸로 배웠으면 이제 당신도 늙은이
대응
함수의 그래프
일차함수
x의 최고차항의 차수가 1인 함수를 말한다. 일차함수의 형태는 크게 두 가지가 있다.
- 표준형 : [math]\displaystyle{ y=mx+n }[/math]
- 일반형 : [math]\displaystyle{ ax+by+c=0 }[/math]
사실 일반형의 식에서 by를 우변으로 이항한 후 양변을 '-b'로 나누어 정리하면 표준형의 꼴이 나오므로 사실은 같은 것이다. 다만, 두 가지가 모두 자주 언급되므로 두 가지 방식으로 설명하겠다. 만약에 너무 어려워서 "두 개는 못 외우겠다."라고 생각한다면 첫 번째인 표준형만을 암기하고, 일반형은 이항하여 표분형으로 만들어서 문제를 해결하면 될 것이다.
- 표준형 : [math]\displaystyle{ y=mx+n }[/math]에서 [math]\displaystyle{ m }[/math]은 함수의 기울기, [math]\displaystyle{ n }[/math]은 y절편을 의미한다.
- 기울기 : 기울기는 함수가 좌표평면 상에서 얼마나 기울어져 있느냐를 알려주는 것으로, m=(y 증가량)/(x 증가량)이다. 만약에 기울기가 m=0이면, 일차함수의 그래프는 x축에 평행하고 m>0이면 위로 올라가는 그래프, m<0이면 아래로 내려가는 그래프를 그린다.
- y절편 : 그래프가 y축과 만나는 점을 의미한다. 즉, x=0을 대입하였을 때의 y 값이다.
이차함수
고차함수
지수와 지수함수
n,m이 실수이고 a>0,b>0일 때 다음이 성립한다.
[math]\displaystyle{ \definecolor{asd}{RGB}{141,117, 0} \color{asd}{{a}^{n+m}={a}^{n}\times {a}^{m}} }[/math]
[math]\displaystyle{ \definecolor{asd}{RGB}{177,117, 0} \color{asd}{{a}^{n-m}=\frac{{a}^{n}}{{a}^{m}}} }[/math]
[math]\displaystyle{ \definecolor{ae}{RGB}{19, 75, 98}\color{ae}{{a}^{nm}={({a}^{m})}^{n}} }[/math]
[math]\displaystyle{ \definecolor{ae}{RGB}{190, 75, 98}\color{ae}{{(ab)}^{n}={a}^{n}\times {b}^{n}} }[/math]
로그와 로그함수
수열
극한
수열의 극한
급수
함수의 극한
극한에 들어가기에 앞서 일러두고 싶은 점은 극한은 엄밀하게 따지려하기 보다는 그냥 직관적으로 받아들이라는 것이다. 무한은 유한과는 전혀 다른 세상이라 유한에서 말도 안 되는 일이 무한에서는 당연하다는 듯이 일어나는 경우가 많다. 그러다보니 얕은 지식으로 깊에 들어가려고 하면 여러 부분에서 개념의 혼선을 빚게 되는 경우가 생긴다. 그러므로 극한의 엄밀한 정의는 해석학을 연구하는 수학자들에게 맡기자.
자 여기에 1/x 가 있는데, 여기서 x가 점점 커진다고 해 보자. x = 100, 10,000, 100,000,000... 이 되면 1/x = 0.01, 0.000,1, 0.000,000,01…이 될 것이다. 이렇게 쭉 해 보면, x가 커지면 커질수록 1/x 는 0에 한없이 가까워진다(적당히 가까워지면 안 된다. 한없이 가까워져야 한다). 유식한 말로 하면, ‘x 가 무한히 커지면 1/x 는 0에 수렴한다(converges)’고 한다. 기호로는 이렇게 쓴다.
[math]\displaystyle{ \lim_{x \to \infty} \frac{1}{x} = 0 }[/math]
x 가 무한대에 가까워질 때 그 극한(limit) 은 0에 가까워진다는 것이다. 0이 되는 것은 아니지만, 0을 목표로 가까이 간다는 소리다. 마치 아무리 공부해도 100점에 도달하지는 못하지만, 목표는 100점으로 잡는 것과 같다.
이번에는 x가 무한대가 아니라 유한한 값에 가까이 가는 것을 생각해 보자. 예를 들어 [math]\displaystyle{ \frac{x^2 - 1}{x - 1} }[/math]에서 x 가 1에 가까이 간다고 해 보자. x = 1 을 대입하면 분자도 분모도 0 이 되니까 답이 없을 것 같지만, 1이 아닌 x = 0.9, 0.999, 0.999,99... 를 대입해 계산기를 두드려 보면, 저 값은 1.9, 1.999, 1.999,99…가 나온다. 생각해 보면 [math]\displaystyle{ \frac{x^2 - 1}{x - 1} = \frac{(x + 1)(x - 1)}{x - 1} = x + 1 }[/math]이 되기 때문에 당연하다. 힝 속았지? 하지만 주의해야 할 것은 우리가 1이 아닌 x의 값만을 생각하고 있기 때문에 x−1이 0이 아니게 되므로 약분을 할 수 있다는 것이다. 만약 x가 진짜로 1이었으면 이렇게 약분하지 못했을 것이다. 하여튼 이걸
[math]\displaystyle{ \lim_{x \to 1} \frac{x^2 - 1}{x - 1} = 2 }[/math]
라고 쓴다. 이처럼 극한은 x가 1이 아닌 값을 가질 때의 함수값을 토대로 x가 1에 한없이 가까워지면 함수값은 대체 어떤 값에 한없이 가까워질까?를 탐구하는 것이다.
이번엔 좀 어려운 걸로, [math]\displaystyle{ \frac{\sin x}{x} }[/math] 에서 x 가 0에 가까워지는 경우를 생각해 보자. 엄밀한 증명(삼각함수의 합차공식이 필요하다)은 생략하고 계산기를 두드려 x = 0.1, 0.01, 0.001... 을 넣어 보면 저 값은 0.998,334,16…, 0.999,983,33…, 0.999,999,83…, …이 된다. 점점 커지면서 1에 한없이 가까워지지만, 1이 되거나 1을 넘어가지는 않는다. 따라서
[math]\displaystyle{ \lim_{x \to 0} \frac{\sin x}{x} = 1 }[/math]
이다. 이걸 다른 말로 풀면, x 가 아주 작아서 0 에 가까울 때 sin x 는 x와 거의 같다는 말도 된다.
위와 같이 어떠한 함수에 극한을 취했을 때, 그 극한값이 특정한 값으로 가는 경우를 수렴, 그렇지 않는 경우를 발산이라고 한다. 이 때 발산은 값이 수렴하지만 않으면 되므로 극한값이 [math]\displaystyle{ \infty }[/math]인 경우와 [math]\displaystyle{ -\infty }[/math]인 경우, 그리고 진동하는 경우를 포함한다.
그래프를 예로 들어 설명하면 [math]\displaystyle{ \lim_{x \to a} f(x) }[/math]이란, 어떠한 함수 f(x)의 그래프를 따라 x가 a에 도달할 때 도착하는 점의 y값이라고 볼 수 있다.(함수에서 최대값, 극대값, 극한값 처럼 값이 들어가는 것은 죄다 y값을 의미한다.) 이 때, a 지점에 도착할 수 있는 방향은 두 가지가 있는데 하나는 a의 왼쪽으로부터 다가오는 것이고, 다른 하나는 a의 오른쪽으로부터 다가오는 것이다. 이를 각각 좌극한과 우극한이라고 부르고 다음과 같이 표기한다.
좌극한 : [math]\displaystyle{ \lim_{x \to a-0} f(x) }[/math] 우극한 : [math]\displaystyle{ \lim_{x \to a+0} f(x) }[/math]
이 때 좌극한과 우극한이 서로 다르다면 과연 극한값은 무엇일까? 대답하기가 곤란한 질문이다. 그래서 이렇게 좌극한과 우극한이 다른경우 쿨하게 극한값이 존재하지 않는다고 표현한다. 즉, 극한값이 존재하기 위해서는 좌극한과 우극한이 같아야 한다.
[math]\displaystyle{ \lim_{x \to a-0} f(x)=\lim_{x \to a+0} f(x)=\alpha \to \lim_{x \to a} f(x)=\alpha }[/math]
그리고 혹시나 하여 첨언하자면 예를 들어 x가 무한대로 갈 때의 극한이 0이라고 할 때, 무한대가 아닌 x의 값에 대해서 함수값이 0이 아니어야만 될 필요는 전혀 없다. 예를 들어 [math]\displaystyle{ \lim_{x \to \infty} 0 = 0 }[/math]이다. 무한대가 아닐 때 계속 0이니까 x가 무한대로 갈 때의 극한도 0인 것이다. x가 유한한 값으로 갈 때도 마찬가지이다.
함수의 극한의 성질
극한의 성질은 극한값이 수렴하는 함수를 전제로 한다. [math]\displaystyle{ \lim_{x \to a} f(x)=\alpha }[/math], [math]\displaystyle{ \lim_{x \to a} g(x)=\beta }[/math]라면, 다음의 수식들이 성립된다.
- [math]\displaystyle{ \lim_{x \to a} cf(x)=c\lim_{x \to a} f(x)=c\alpha }[/math]
- [math]\displaystyle{ \lim_{x \to a} f(x) \pm g(x)=\lim_{x \to a} f(x) \pm \lim_{x \to a} g(x)=\alpha\pm\beta }[/math]
- [math]\displaystyle{ \lim_{x \to a} f(x) \times g(x)=(\lim_{x \to a} f(x))\times(\lim_{x \to a} g(x))=\alpha\times\beta }[/math]
- [math]\displaystyle{ \lim_{x \to a} \frac{f(x)}{g(x)}=\frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}=\frac{\alpha }{\beta } }[/math] (단, [math]\displaystyle{ \beta\neq 0 }[/math])
- 단! 분모 [math]\displaystyle{ \beta }[/math]가 '0'이 아닐때만! 이것이 중요하다. 분모가 0일수는 없지 않은가. 그러므로 4번 성질은 분모가 0이 아닐때만 성립한다.
중요하니까 두번 말했다.
- 단! 분모 [math]\displaystyle{ \beta }[/math]가 '0'이 아닐때만! 이것이 중요하다. 분모가 0일수는 없지 않은가. 그러므로 4번 성질은 분모가 0이 아닐때만 성립한다.
- [math]\displaystyle{ f(x)\lt g(x) }[/math]이면 [math]\displaystyle{ \alpha \leq \beta }[/math]
- 처음에 두 함수의 크기관계가 [math]\displaystyle{ f(x)\lt g(x) }[/math]였더라도 극한을 보내면 그 극한값이 같을 수도 있다. 예를 들어 [math]\displaystyle{ \frac{1}{x}\lt \frac{2}{x} }[/math]이지만 극한값은 0으로 동일하다.
즉, 극한이 수렵함다면 실수배, 더하기, 빼기, 곱하기, 나누기가 모두 허용되나 나눌 때는 분모가 0이 아니어야 한다.
위의 성질 중 4번, 5번이 확답형에 자주 나오는 문항이다. 주로 다음과 같이 묻는다.
- [math]\displaystyle{ \lim_{x \to a} f(x)g(x)=\alpha,\lim_{x \to a} f(x)=\beta }[/math]이면, [math]\displaystyle{ (\lim_{x \to a} g(x)) }[/math]는 수렴하는가?
이는 [math]\displaystyle{ \lim_{x \to a} f(x)g(x) }[/math]를 [math]\displaystyle{ \lim_{x \to a} f(x) }[/math]로 나누어도 되는지를 묻는 문제이며, [math]\displaystyle{ \beta }[/math]가 0이라는 보장이 없으므로 틀린 명제이다.
미분
미분이라는 것은 간단히 말하면 적분의 반대 개념이다. 그리고 적분은 미분의 반대 개념이다. 미분이 계산하기 편하기 때문에 먼저 배우는 경우가 많은데, 사실 직관적으로 원리를 설명하기 편리한 쪽은 도형의 넓이를 구한다던지 하는 데에 쓰이는 적분이다.

자동차가 0 m 의 출발선에서 출발해서, 1초 후에 1 m, 2초 후에 4 m, 3초 후에 9 m ... 를 간다고 해 보자. 그러면 10초 후에는 100 m 를 갔을 것이고, 속력을 계산해 보면 속력은 거리/시간 이니까 100 m / 10초 = 10 m/s 가 된다. 그런데 이건 '10초 동안의 평균 속력' 이지, '10초가 된 순간에 자동차 계기판에 찍힌 순간 속력' 은 아니다. 10초가 된 순간의 속력을 알고 싶으면 어떻게 해야 할까?
생각해 보면, 9초일 때 자동차의 위치는 81 m, 9.9초일 때는 98.01 m, 9.99초일 때는 99.8001 m... 이다. 그러면 자동차의 속력은 (100 - 81 m)/(10 - 9초), (100 - 98.01 m)/(10 - 9.9초), (100 - 99.8001 m)/(10 - 9.99초)... 가 될 것이다. 앞에서 한 것과 비슷하지 않은가?
수식으로 정리해 보면, [math]\displaystyle{ \lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} }[/math] 이다. 인수분해해서 계산하면
[math]\displaystyle{ \lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} = \lim_{x \rightarrow 10}\frac{(10 + x)(10 - x)}{10 - x} = \lim_{x \rightarrow 10}(10 + x) = 20 }[/math]
즉 10초가 된 순간의 자동차의 속력이 20 m/s 임을 함수의 극한을 이용해 구한 것이다. 이렇게 어떤 함수의 매 순간의 변화량을 함수의 극한을 통해 구하는 것이 미분이다.
이걸 좀더 일반화해 보자. 시간 x 초에서 자동차가 간 거리는 x2 이다. 그러면 x 초에서의 속력을 알기 위해, x 보다 약간 작은 x - h 초를 생각해 보면, x - h 초일 때의 거리는 (x - h)2 가 될 것이고, 위에서 한 것처럼 순간 속력은 h 가 0 에 가까워져 x 와 x - h 가 아주 가까워질 때를 생각하면 된다.
[math]\displaystyle{ \lim_{h \rightarrow 0}\frac{x^2 - (x - h)^2}{x - (x - h)} = \lim_{h \rightarrow 0}\frac{x^2 - x^2 + 2hx - h^2}{h} = \lim_{h \rightarrow 0}(2x - h) = 2x }[/math]
따라서 x 초가 된 순간의 자동차의 속력은 2x m/s 이다. 매번 9, 9.9, 9.99... 의 제곱을 구해서 100에서 빼고 나누고 하는 귀찮은 짓을 할 필요 없이, 이제 10초일 때의 속력은 20, 20초일 때는 40... 이렇게 바로 구할 수 있게 된 것이다! 이게 바로 '함수를 미분' 한 것이다.
미분이라는 것은 어떤 함수 [math]\displaystyle{ f(x) }[/math]가 있을 때 [math]\displaystyle{ (x, f(x)) }[/math]에서 [math]\displaystyle{ f(x) }[/math]와 접하는 선, 즉 접선의 기울기를 구할 때에 사용된다.
이를 어떻게 구하는지 보자. [math]\displaystyle{ f(x) }[/math] 함수 위의 두 점, [math]\displaystyle{ (a, f(a)) }[/math]와 [math]\displaystyle{ (b, f(b)) }[/math]를 지나는 선의 기울기는 다음과 같을 것이다.
기울기 : [math]\displaystyle{ \frac{f(b) - f(a)}{b-a} }[/math]
이를 그대로 적용해서, 점 [math]\displaystyle{ (x, f(x)) }[/math]와 그로부터 x축으로 [math]\displaystyle{ \Delta x }[/math]만큼 떨어진 [math]\displaystyle{ (x+\Delta x, f(x+\Delta x)) }[/math] 의 기울기를 표현하면 다음과 같을 것이다.
기울기 : [math]\displaystyle{ \frac{f(x+\Delta x) - f(x)}{ (x + \Delta x) - x} = \frac{f(x+\Delta x) - f(x)}{ \Delta x} }[/math]
이 때 [math]\displaystyle{ \Delta x }[/math]가 작아질수록 이 두 점을 연결하는 선은 점점 우리가 구하고자 하는 접선의 기울기에 가까워지게 된다. 따라서, 함수 [math]\displaystyle{ f(x) }[/math]의 접선의 기울기는 다음과 같이 표현할 수 있다.
접선의 기울기 : [math]\displaystyle{ \lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x) - f(x)}{ \Delta x} }[/math]
이를 함수 f(x)의 도함수라고 하며, [math]\displaystyle{ f'(x) }[/math] 또는 [math]\displaystyle{ \frac {\mathrm dy}{\mathrm dx} }[/math]라고 표기한다. 전자는 함수 f의 도함수라는 것을 표현한 것이며, 후자는 접선의 기울기를 나타낸다는 것을 표현한 것이다. 문제에 따라서 편리한 표현방법을 사용하게 된다.
다항함수의 미분법
다항함수의 미분법은 아주 간단하다. 빼기, 곱하기만 할 수 있으면 누구나 할 수 있다. 물론 그 증명도 중요하지만 일단 계산법만 올려보자면 아래와 같다.
함수 [math]\displaystyle{ \definecolor{asd}{RGB}{255,0, 0} \color{asd}{{x}^{n}} }[/math]의 도함수는 다음과 같다.[5]
[math]\displaystyle{ \definecolor{asd}{RGB}{255,0, 0} \color{asd}{f(x)={x}^{n} \to f'(x)=n{x}^{n-1}} }[/math].
[math]\displaystyle{ \definecolor{asd}{RGB}{255,0, 0} \color{asd}{\frac{\mathrm d}{\mathrm dx}({x}^{n})=n{x}^{n-1}} }[/math]
다음과 같은 계산 과정을 통해서 자연수에 대해서 증명이 가능하고, 미분에 대한 지식 몇 가지만 추가하면 실수 n에 대해서 확장할 수 있다. 그러나 어렵다 싶으면 일단 그냥 암기해서 이용해도 문제없는 부분이다.
[math]\displaystyle{ \lim_{\Delta x\rightarrow 0} \frac{(x+\Delta x)^n - x^n}{\Delta x} = \lim_{\Delta x\rightarrow 0} \frac{nx^{n-1}\Delta x+1/2n(n-1)x^{n-2}\Delta x^2 + ... + nx\Delta x^{n-1} + \Delta x^n }{\Delta x} }[/math]
[math]\displaystyle{ \Delta x }[/math]는 0에 무한히 가깝게 가지만 0은 아니므로 약분할 수 있고, 그러면 [math]\displaystyle{ \Delta x }[/math]의 2차항 이상은 극한이 0으로 가므로 무시할 수 있어서, 위 함수의 도함수는 [math]\displaystyle{ n{x}^{n-1} }[/math]이 된다는 것을 알 수 있다. 이것을 미분에 있어서의 Power Rule, 한잣말로 지수법칙이라고 부른다.
다음은 아래에 나오는 로그함수에 대한 법칙을 이용해서 지수법칙을 실수 n에 대해 증명하는 방법이다. 이 경우에는 또 로그법칙을 알고 있어야 한다는 점이 문제이지만...
[math]\displaystyle{ y = x^n }[/math]
[math]\displaystyle{ \ln y = n \ln x }[/math]
양변을 미분하면
[math]\displaystyle{ \frac{1}{y}\frac{\mathrm dy}{\mathrm dx} = \frac{n}{x} }[/math]
[math]\displaystyle{ \frac{\mathrm dy}{\mathrm dx} = \frac{n}{x}y }[/math]
[math]\displaystyle{ y= x^n }[/math]이므로 이를 다시 위의 수식에 치환하면
[math]\displaystyle{ \frac{\mathrm dy}{\mathrm dx} = \frac{n}{x} x^n = n x^{n-1} }[/math]
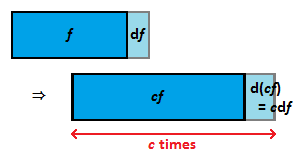
상수배
[math]\displaystyle{ \definecolor{asd}{RGB}{255,0, 0} \color{asd}{\frac{\mathrm d}{\mathrm dx}(cf(x))=c\frac{\mathrm d}{\mathrm dx}(f(x))} }[/math]
그림에서 [math]\displaystyle{ \mathrm d(cf) = c\mathrm df }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(cf)}{\mathrm dx} = c \frac{\mathrm df}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
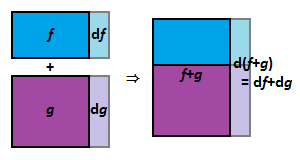
합차
[math]\displaystyle{ \definecolor{asd}{RGB}{110,41, 150} \color{asd}{\frac{\mathrm d}{\mathrm dx}(f(x) \pm g(x))=\frac{\mathrm d}{\mathrm dx}(f(x)) \pm \frac{\mathrm d}{\mathrm dx}(g(x))} }[/math]
그림에서 [math]\displaystyle{ \mathrm d(f+g) = \mathrm df+\mathrm dg }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(f+g)}{\mathrm dx} = \frac{\mathrm df}{\mathrm dx} + \frac{\mathrm dg}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
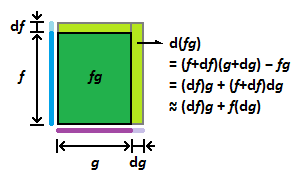
곱
[math]\displaystyle{ \definecolor{asd}{RGB}{44,125, 150} \color{asd}{\frac{\mathrm d}{\mathrm dx}(f(x)g(x))=\frac{\mathrm d}{\mathrm dx}(f(x))g(x)+f(x)\frac{\mathrm d}{\mathrm dx}(g(x))} }[/math]
그림에서 [math]\displaystyle{ \mathrm d(fg) = (\mathrm df)g+f(\mathrm dg) }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(fg)}{\mathrm dx} = \frac{\mathrm df}{\mathrm dx} g + f \frac{\mathrm dg}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
왜 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]를 무시해도 되는지는 좀 설명이 필요하다. 지금 [math]\displaystyle{ \mathrm df }[/math]랑 [math]\displaystyle{ \mathrm dg }[/math] 모두 [math]\displaystyle{ \mathrm dx }[/math]가 줄어듦에 따라 같이 줄어든다. 따라서 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]는 [math]\displaystyle{ \mathrm df }[/math]가 줄어드는 속도와 [math]\displaystyle{ \mathrm dg }[/math]가 줄어드는 속도의 영향을 중첩적으로 받아 훨씬 빨리 줄어들게 된다. 즉 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]가 줄어드는 속도가 [math]\displaystyle{ \mathrm dx }[/math]가 줄어드는 속도보다 한층 빠르고, 따라서 무시해도 되는 것이다. 즉 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]가 작아서 무시한다는 말은 좀 그렇고, 작긴 작은데 그 정도가 [math]\displaystyle{ \mathrm dx }[/math]보다 한층 더하기 때문에 무시해도 된다는 것이다.
합성함수
y=f(u)이고,u=g(x)이고 둘 다 미분가능하면.
[math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 150} \color{asd}{\frac{\mathrm dy}{\mathrm dx}=\frac{\mathrm dy}{\mathrm du}\times \frac{\mathrm du}{\mathrm dx}} }[/math][6]
삼각함수
사인
[math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 197} \color{asd}{\frac{\mathrm d}{\mathrm dx}(\sin x)=\cos x} }[/math].
코사인
[math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 202} \color{asd}{\frac{\mathrm d}{\mathrm dx}(\cos x)=-\sin x} }[/math].
탄젠트
[math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 209} \color{asd}{\frac{\mathrm d}{\mathrm dx}(\tan x)={\sec }^{2} x} }[/math].
역함수
임의의 함수 [math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 150} \color{asd}{f(x)} }[/math]의 역함수
[math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 150} \color{asd}{{f}^{-1}(x)} }[/math] 가 존재하면.
[math]\displaystyle{ \definecolor{asd}{RGB}{255,1, 150} \color{asd}{\frac{\mathrm d}{\mathrm dx}({f}^{-1}(x))=\frac{1}{f'({f}^{-1}(x))}} }[/math].
지수함수
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}e^x = e^x }[/math]
[math]\displaystyle{ \definecolor{asd}{RGB}{81,64, 242} \color{asd}{\frac{\mathrm d}{\mathrm dx}({a}^{x})={a}^{x}\ln a} }[/math].
[math]\displaystyle{ \definecolor{ers}{RGB}{81,64, 242} \color{ers}{a\neq 1,a\gt 0} }[/math].
로그함수
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}\ln x = \frac{1}{x} }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx} \log_{a} x = \frac{1}{x \ln {a}} }[/math]
평균값 정리
도로교통 이야기로 잠시 넘어가보자. 구간단속은 일정 구간에서 평균 속도가 제한 속도를 위반하면 적발하는 단속 방법이다. 이전까지 쓰이던 지점단속에는 단속 대상자가 카메라 앞에서만 속도를 잠시 줄인 뒤 카메라에서 벗어나면 다시 과속을 할 수 있다는 문제가 있었다. 그러나 구간단속에서는 이런 꼼수가 원천 차단된다.
예를 들어 어떤 운전자의 차량이 적발 속도가 80km/h이고 길이가 1km인 구간단속 시작지점에 들어설 때 시속 60km으로 달리고 있었다고 가정하고 30초 후 끝지점으로 나올 때 여전히 시속 60km로 달리고 있었다고 가정하자. 이때 이 차량의 평균 속도는 120km/h이다. 이 결과는 단속구간에 있을 때 어느 순간 차량의 순간속도가 120km/h을 찍었다는 걸 의미한다. 지점단속으로는 단속에 걸리지 않지만 구간단속으로는 얄짤없이 단속에 걸리게 된다. 이 상황을 약간 추상화하면, 어느 구간에서 (구간 양끝 함수값의 차)/(구간 양끝점의 차)의 값과 같은 미분계수를 가지는 지점이 존재한다는 결론을 얻고, 이것이 바로 평균값 정리다. 물론 아무 때나 쓰면 곤란하고 평균값 정리가 성립하기 위한 조건들이 있으니, 더 자세히 알고 싶으면 항목을 참조하길.
적분
경우의 수, 확률 및 통계
경우의 수
확률
- 확률에서 가장 큰 오해는, 확률 자체가 우리가 관측한 값으로 계산을 하는것이지, 우리가 관측한 값을 토대로 예측을 하는것이 아니다. 이 오해를 풀지 못하면 아래 통계에서도 엄청나게 고생을 한다. 이거 하나만 이해해도 확률에서 배울 내용의 50%는 배운거라고 할 수 있다.
- 가장 대표적인 예로, 주사위에서 숫자 1이 나올 확률은 6분의 1이다. 하지만 주사위 10번을 던졌는데 그중 1이 한번도 안나왔다고 해서 다음번에 숫자 1이 나올 확률이 급상승 하는것은 절대 아니다!!
사기도박을 의심해야한다. 오함마 가져와야지 - 그러면 왜 1이 안나왔는지에 대한 분석을 해야하는데, 그걸 분석하는것이 바로 통계다
이게 정확한 통계의 정의는 아니다. 물론 확률과 통계가 수학에 기초를 둔 만큼, 이 증명과정을 역으로 써서 예측을 할 수는 있으나, 그게 꼭 맞는다는 보장을 하려면 실제 결과가 나오고 그 관측값을 토대로 증명을 해야하기 때문에 절대 쉬운일이 아니다.그게 가능하면 모두다 로또 1등이고 주식 대박이다
- 가장 대표적인 예로, 주사위에서 숫자 1이 나올 확률은 6분의 1이다. 하지만 주사위 10번을 던졌는데 그중 1이 한번도 안나왔다고 해서 다음번에 숫자 1이 나올 확률이 급상승 하는것은 절대 아니다!!
통계
- 대학생 과정의 통계에서 가장 중요한 건 내가 어떤 학문의 통계를 하느냐이다. 통계식을 최종적으로 정리하는 과정에서 사용되는 상수들은 각 학문의 영역마다 다른데, 당장 생물학만 하더라도 생물 개체를 실험하는 경우는 생물실험통계를, 생화학적인 부분을 입증할때에는 화학실험통계를, 생태계를 조사할때에는 사회통계를 끌어다쓴다.
그래서 생물학 관련과들은 수학공부는 좀 덜해도 통계공부하기 지옥이다. - 바꿔 말하자면, 고등학생과정에서 배우는 통계는 좀 잡소리가 많지만 이런 통계의 공통분모만을 간단하게 배우는것이다. 실제 계산을 하는것보다는 외우는게 많으며, PK/SKY급 학교가 아닌이상 대부분 통계 첫 시간에 이런 내용을 다시 가르치는것이 일반적이기 때문에, 고등학교 통계를 모른다고 해서 학사 스케줄이 꼬일정도의 문제가 되진 않는다.
물론 그걸 하루 수업으로 압축했다는 사실은 꼭 기억해야한다. 일주일안에 따라잡아야한다. - 이공계열 대학생 과정에서의 통계만 이야기를 하자면, 실제의 통계 계산은 대부분 프로그램에 맏긴다. 하지만 처음에는 대부분 통계 용어의 정의를 하는데, 이 정의는 따로 답이 없다. 그냥 이런게 있다고 외우는 수 밖에 없다. 사실 이걸 증명하는것까지 하면 좋지만, 대부분의 통계프로그램은 그 통계증명이 된 상황이다. 우리가 그걸 실제로 할 필요는 없다. 하지만 그 용어의 정의를 인식하지 못하면 통계프로그램을 쓸 수조차 없다.
고등학교 다닌지 오래돼서 정확한지는 모르겠지만고등학교 통계에서 결국 가르치는건 이런 통계학에서 써먹는 기초적인 정의를 가르치는 것이다. 실제로 계산은 큰 의미가 없으니 일단 단어의 정의정도는 꼭 외워두자. 여유가 되면 그 평균이나 표준편차의 계산정도는 외워두는것이 매우 큰 도움이 된다.- 가장 중요한 내용. 통계는 주관적인 학문이다. 보통 수학의 범주안에 넣지만, 실제로는 어떤 공식을 적용하여도 결과가 나오고, 그게 맞는지 틀리는지는 또 통계로 증명을 해야하는데 그게 또 완성되기 매우 쉽다. 공식을 잘못 넣으면 계산 자체가 안되고, 증명도 완성 안되는 다른 수학과는 다르게 통계는 뭘 넣어도 결과가 나오고 증명이 되기 때문에 어떤식으로 접근하여 분석의 신뢰도를 적당하게 올리느냐(이건 통계에서 일반적으로 쓰이는 신뢰범위와는 다르다)가 가장 중요하다. 실제로 가장 많이 일어나는것이, 임의로 분석의 신뢰도를 내려서 논문을 쓰는 경우가 많고, 이 경우 아무리 좋은 실험을 했다 한들 믿을수 없는 실험이 된다. 이상적인 통계환경에서는 이 분석의 신뢰도가 정해져 있지만, 현실은 그렇지 않기 때문에 어느정도까지 신뢰도를 잡을것이냐가 통계의 핵심이 된다. 이걸 이해한다면 통계가 들어가는 논문을 쓸 자격이 있다는 말이 된다.(...)
이 항목을 쓴 사람은 이과에서 수능 7등급받고 생물학 전공으로 튀다가 통계로 엿먹어본 사람이다.
집합과 명제
일단 집합이 쉬운 개념은 아니라는 것부터 인식할 필요가 있다. 다들 그다지 어렵게 생각 안해서 그렇지 집합이란 사실 대단히 추상적인 개념으로, 대단히 최근에(예를 들어 미적분보다 더 요즘) 생겨난 개념이다. 만일 이 단원이 어렵지 않게 느껴진다면 이미 수학적 사고와 추상화에 대단히 익숙해져 있기 때문이다. 거기에 익숙하지 않은 사람들은 당연히 이 단원이 어렵다!
집합은 결국 수학적 엄밀성과 연결되어 있다. 칸토어가 수학적 엄밀성을 추구하다보니 집합이란 개념이 생각난 것이고, 이는 1960년대의 새수학 운동과도 연결되어 있으므로, 이 단원을 언제 가르쳐야 할지 현재 애매한 상태이다. 현재는 수학II 교과에서 가르친다.
간단히 말해서, 집합이란 건 모임이다. 우리 가족의 모임을 예로 들면 울아빠, 울엄마, 나, 우리동생 이렇게 표현할 수 있는 것 처럼 이를 기호로 우리 가족={울아빠, 울엄마, 나, 우리동생} 이렇게 표현한 것이다. 그런데, 유의할 점이, 집합 안에도 원소로 집합이 들어갈 수 있다는 점이다. 예를 들면, 추석 때 모이는 친족 모임={우리 가족, 큰아버지 가족, 작은아버지 가족} 이런 방식으로 가족이라는 집합을 원소로 또 다른 집합을 만들 수 있는 것이다. 여기서 헷갈리지?
- 공집합: 원소가 하나도 없는 집합. 기호는 [math]\displaystyle{ \{ \} }[/math]나 [math]\displaystyle{ \emptyset }[/math].
[math]\displaystyle{ \phi }[/math]와는 다르다 [math]\displaystyle{ \phi }[/math]와는 - 전체집합: 고려해야하는 모든 대상을 담은 집합. 기호로는 보통 [math]\displaystyle{ \operatorname U }[/math](universal set)를 쓴다. 공집합의 여집합은 전체집합이다. 왜(?)