개요
한국의 수학 교육과정상 중학교 때 배우게 되는 기하학 정리. 다만 교과서에는 방멱의 정리라는 알아 듣기 힘든 이름 대신 원과 직선에 관한 정리라는 이름으로 배우게 된다. 여기서 방멱(方冪)이란, 어떤 한 점 [math]\displaystyle{ P }[/math]를 지나는 직선이 어떤 원 [math]\displaystyle{ O }[/math]와 만나는 점을 [math]\displaystyle{ A, B }[/math]라 했을 때, 두 선분의 곱 [math]\displaystyle{ \overline{PA}\times\overline{PB} }[/math]를 가르킨다. 방멱의 정리는 크게 3가지가 있다. 3가지 모두 평면기하학 관련 문제에서 의외로 자주 쓰이므로 잊어버리지 않도록 하자.
두 현에 대한 방멱
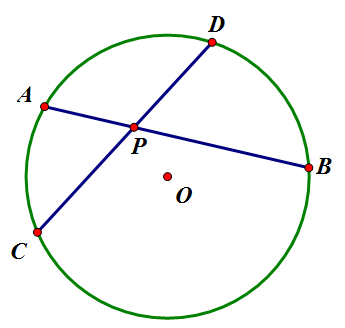
“ 두 현 [math]\displaystyle{ \overline{AB},\overline{CD} }[/math]의 교점을 [math]\displaystyle{ P }[/math]라 하자. 그러면 [math]\displaystyle{ \overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD} }[/math]가 성립한다. “
증명
[math]\displaystyle{ \angle{ACP}=\angle{DBP} }[/math] (호 [math]\displaystyle{ \overarc{AD} }[/math]에 대한 원주각) [math]\displaystyle{ \angle{CAP}=\angle{BDP} }[/math] (호 [math]\displaystyle{ \overarc{BC} }[/math]에 대한 원주각) [math]\displaystyle{ \therefore\triangle{APC}\sim\triangle{DPB} }[/math] (AA 닮음) [math]\displaystyle{ \overline{PA}:\overline{PD}=\overline{PC}:\overline{PB} }[/math]
[math]\displaystyle{ \therefore\overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD} }[/math]
두 할선에 대한 방멱
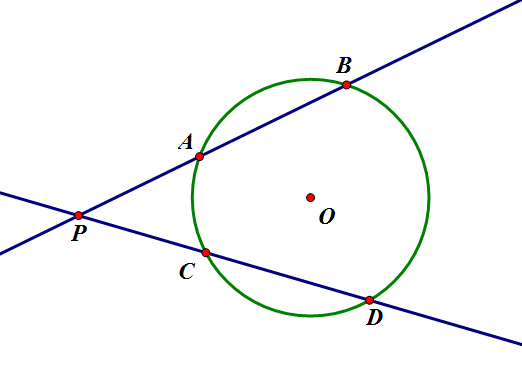
“ 두 할선 [math]\displaystyle{ \overleftrightarrow{AB},\overleftrightarrow{CD} }[/math]의 교점을 [math]\displaystyle{ P }[/math]라 하자. 그러면 [math]\displaystyle{ \overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD} }[/math]가 성립한다. “
증명
[math]\displaystyle{ \angle{PBC}=\angle{PDA} }[/math] (호 [math]\displaystyle{ \overarc{AC} }[/math]에 대한 원주각) [math]\displaystyle{ \angle{BPD} }[/math] 공통 [math]\displaystyle{ \therefore\triangle{PBC}\sim\triangle{PDA} }[/math] (AA 닮음) [math]\displaystyle{ \overline{PB}:\overline{PD}=\overline{PC}:\overline{PA} }[/math]
[math]\displaystyle{ \therefore\overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD} }[/math]
할선과 접선에 대한 방멱
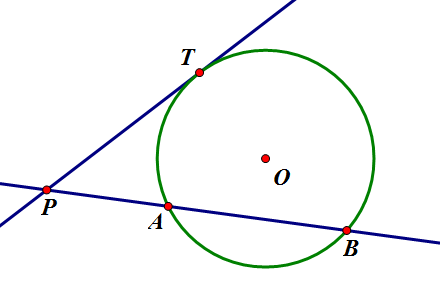
“ 할선 [math]\displaystyle{ \overleftrightarrow{AB} }[/math]와 원 [math]\displaystyle{ O }[/math]의 접선 [math]\displaystyle{ \overleftrightarrow{PT} }[/math]가 점 [math]\displaystyle{ P }[/math]에서 만난다고 하자. 그러면 [math]\displaystyle{ \overline{PA}\times\overline{PB}=\overline{PT}^2 }[/math]가 성립한다. “
증명
[math]\displaystyle{ \angle{PTA}=\angle{PBT} }[/math] (접현각) [math]\displaystyle{ \angle{TPB} }[/math] 공통 [math]\displaystyle{ \therefore\triangle{PTA}\sim\triangle{PBT} }[/math] (AA 닮음) [math]\displaystyle{ \overline{PT}:\overline{PB}=\overline{PA}:\overline{PT} }[/math]
[math]\displaystyle{ \therefore\overline{PA}\times\overline{PB}=\overline{PT}^2 }[/math]
방멱의 정리의 역
피타고라스 정리의 역과 비슷하게 방멱의 정리에도 역이 있다.
“ 두 선분 [math]\displaystyle{ \overline{AB},\overline{CD} }[/math] 혹은 그 연장선의 교점 [math]\displaystyle{ P }[/math]에 대해서 [math]\displaystyle{ \overline{PA}\times\overline{PB}=\overline{PC}\times\overline{PD} }[/math]가 성립하면 네 점 [math]\displaystyle{ A,B,C,D }[/math]는 공원점이다. “
증명은 의외로 간단한데, 위 식을 비례식으로 바꿔준 뒤, 두 삼각형이 닮음이란 것을 보이고,[* [math]\displaystyle{ P }[/math]가 두 선분의 교점이냐 연장선의 교점이냐에 따라서 닮음인 삼각형이 달라진다.] 원주각이 성립함을 보이면 끝.