마방진

마방진(魔方陣, Magic Square)은 각 원소가 n²의 수로 이루어져 있고, 각 행의 원소의 합과 각 열의 원소의 합, 그리고 주대각선에서의 n개의 원소의 합이 모두 같은 n×n 정사각행렬을 의미한다. 원소의 조건은 n²의 연속된 숫자를 의미하는 경우가 많으나 상황에 따라 다른 것을 의미할 수도 있다.

마방진의 개수

1차 마방진은 1 하나의 원소로 된 마방진이며, 2차 마방진은 존재하지 않는다. 3차 마방진은 회전과 대칭이동에 의한 변환을 동일한 것으로 취급할 때 아래에서 언급하는 중국의 로슈방진(Lo Shu Square) 하나뿐이다. 4차 마방진은 회전/대칭이동의 변환에 대해 880가지의 서로 다른 배열이 있다. 5차 마방진은 275,305,224가지 배열이 있으며, 6차 마방진은 정확한 숫자는 알려져 있지 않으나 1.8 × 10¹⁹개가 있다고 추정된다.

역사

마방진은 중국에서 적어도 기원전 7세기부터 알려져 있었고, AD 570년에 처음으로 기록이 남겨져 있다. 또한 5차 마방진과 6차 마방진은 10세기경 이슬람권에서 존재가 알려져 있다.

가장 유명한 마방진은 바로 3*3마방진인 로슈 사각형(Lo Shu Square, wikipedia:Lo Shu Square)이다. 아래와 같은 배열로 구성되어 있다.

2	9	4
7	5	3
6	1	8

유렵

1300년경 비잔틴 제국의 수학자 마누엘 모스코푸로스(Manuel Moschopoulos)가 마방진에 대해서 언급하였다.

1514년 알브레히트 뒤러(wikipedia:Albrecht Dürer)의 작품 멜랑꼴리아(Melencolia I.)에 4차 마방진이 새겨져 있는데 절묘하게도 아랫줄 가운데 두 숫자 15,14가 작품의 제작년도를 나타낸다.

1510년 신비주의 작가인 하인리히 코넬리우스 아그리파(wikipedia:Heinrich Cornelius Agrippa)는 그의 저서 De Occulta Philosophia에서 은둔자와 Marsilio Ficino와 Pico della Mirandola의 경이로운 일에 대해 서술하였다. 1531년 개정판에서는 당시에 알려진 행성과 3*3에서 9*9까지의 마방진을 다음과 같이 연계해서 묘사하였다. 참고로 행성의 순서는 프톨레마이오스의 천동설 기준으로 행성의 배열 순서(먼 행성에서 가까운 행성으로)과 일치한다.

토성=15
4	9	2
3	5	7
8	1	6

목성=34
4	14	15	1
9	7	6	12
5	11	10	8
16	2	3	13

화성=65
11	24	7	20	3
4	12	25	8	16
17	5	13	21	9
10	18	1	14	22
23	6	19	2	15

태양=111
6	32	3	34	35	1
7	11	27	28	8	30
19	14	16	15	23	24
18	20	22	21	17	13
25	29	10	9	26	12
36	5	33	4	2	31

금성=175
22	47	16	41	10	35	4
5	23	48	17	42	11	29
30	6	24	49	18	36	12
13	31	7	25	43	19	37
38	14	32	1	26	44	20
21	39	8	33	2	27	45
46	15	40	9	34	3	28

수성=260
8	58	59	5	4	62	63	1
49	15	14	52	53	11	10	56
41	23	22	44	45	19	18	48
32	34	35	29	28	38	39	25
40	26	27	37	36	30	31	33
17	47	46	20	21	43	42	24
9	55	54	12	13	51	50	16
64	2	3	61	60	6	7	57

달=369
37	78	29	70	21	62	13	54	5
6	38	79	30	71	22	63	14	46
47	7	39	80	31	72	23	55	15
16	48	8	40	81	32	64	24	56
57	17	49	9	41	73	33	65	25
26	58	18	50	1	42	74	34	66
67	27	59	10	51	2	43	75	35
36	68	19	60	11	52	3	44	76
77	28	69	20	61	12	53	4	45

마방진의 종류

4×4방진의 서열

보통 마방진은 행, 열, 그리고 주대각선(main diagonal)에 있는 n개의 원소의 합이 일정한 행렬을 의미한다. 우선 1부터 n²까지의 원소의 합은 n²(n² +1)/2이고, 따라서 각 행/열의 합은 n(n² +1)/2가 성립한다.

1부터 n²까지 숫자를 가진 n×n 방진 중에서 각 행과 열의 합이 동일하기만 하면 준마방진(semimagic square)라고 부르며, 주대각선 n개의 원소의 합이 동일할 때 일반적인 마방진이 된다.

마방진 중에서 좀 더 강력하게 주대각선이 아닌 끊긴 대각선의 원소들의 합 [math]\displaystyle{ \{a_{i,c+i}:i=1,\cdot\cdot\cdotn\}, \{a_{i,n+c-i}: i=1,\cdot\cdot\cdot,n\} }[/math](여기서 c는 0 이상의 상수, i+c>n 또는 n+c-i>n이면 n을 빼준다.)까지도 모두 같으면 완전대각방진(Panmagic Square 혹은 Diabolic Magic square)이라고 부른다. 특이하게도 n=3이거나 n=4k+2꼴일 때에는 완전대각방진이 존재하지 않은 것으로 알려져 있다. (참조 : Wikipedia:Panmagic square)

완전마방진 중에서도 임의의 상수 c,d에 대해 2x2 부분행렬 [math]\displaystyle{ \begin{pmatrix} a_ij & a_{i,j+c} \\ a_{i+d,j} & a_{i+d, j+c} \end{pmatrix} }[/math]의 원소의 합이 2n²+2까지 만족하는 마방진을 Most-perfect Magic square(해석하면 가장 완벽한 마방진)이라고 부른다. (참조: Wikipedia:Most-perfect magic squre)

마방진 중에서도 2 이상의 자연수 p에 대해서 각 원소를 p제곱한 원소들을 모아도 마방진을 이룰 경우 p-제곱 마방진(p-multimagic square)라고 부른다.

다른 조건으로 각 행의 원소의 합, 각 열의 원소의 합, 그리고 두 대각선의 원소의 합을 나열할 때 서로 다른 2n+2개의 연속된 자연수로 나열되는 경우를 Antimagic Square라고 부른다. (참조 : Wikipedia:Antimagic square)

마방진을 만드는 방법

홀수 방진

n*n 마방진을 만드는 가장 간단한 방법은 다음과 같다. 이 방법은 아래에서 설명하는 방법의 특수한 경우라 할 수 있다.

1. 우선 맨 윗줄 가운데에 1을 적는다.
2. 그 다음 오른쪽 칸의 맨 아랫줄에 2를 적는다.
3. 그 다음에 2의 오른쪽/위쪽 1칸 대각선 방향에 3을 적는다. 마찬가지로 4~n까지 숫자가 1개씩 커질 때마다 오른쪽/위쪽 1칸 대각선 방향으로 적는다. 만일 k가 맨 오른쪽 칸에 있을 경우 k+1은 한 줄 위의 맨 왼쪽 칸으로 이동한다.
4. 대각선 방향으로 계속 가면 n+1의 위치는 1과 겹친다. 이 때 n+1은 n의 한 칸 아래칸에 적는다.
5. 1~3번과 같은 방법으로 n+1~2n까지 숫자들은 1씩 커질 때마다 오른쪽/위쪽 1칸 대각선씩 옮겨서 적는다. 역시 k가 맨 윗줄의 숫자인 경우 다음 숫자는 맨 아랫줄의 오른쪽 1칸으로, 맨 오른쪽의 숫자의 경우 다음 숫자는 1줄 위의 맨 왼쪽 칸으로 옮겨서 적는다.
6. 2n+1 역시 n+1과 마찬가지로 2n 한 칸 아래에 적는다. 5번처럼 2n+1~3n의 숫자들을 대각선 ↗방향으로 1칸씩 옮겨가면서 적는다. 마찬가지로 3n+1도 3n의 한 칸 아래에 적고, 3n+1~4n도 마찬가지 방법으로 대각선 방향으로 옮겨가면서 적는다.
7. 6의 과정을 모든 n²개의 칸이 채워질 떄까지 적는다.

위와 같은 방법으로 5×5 마방진을 만들 수 있다. 편의상 (k-1)n+1에서 kn까지의 숫자들은 모두 같은 색으로 칠한다.

5×5 마방진

17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

좀 더 일반화하는 방법을 사용해보자. 일단 이변수 함수
T:{1,..,n}×{1,...,n} → {1,2,...,n²} , T(a,b)=(a-1)n+b
형태로 잡는다. 그러면 T는 일대일 대응인 것을 쉽게 보일 수 있다. 우선 홀수방진은 정가운데 칸 (즉 (n+1)/2열 (n+1)/2행)이 존재한다. 이곳에 k=(n²+1)/2=T((n+1)/2, (n+1)/2)를 집어넣는다. 그 다음에 2줄/1칸 위, 즉 날 일자(日), 혹은 체스의 나이트(knight) 행마와 유사한 형태로 k+1=T((n+1)/2,(n+3)/2)을, 반대로 2줄/1칸 아래 방향으로는 k-1=T((n+1)/2,(n-1)/2)를 집어넣는다. 아래의 그림을 참조하자.

위의 마방진 채우듯 맨 윗줄을 넘길 경우 맨 아랫줄로 넘기고, 맨 오른쪽 칸을 넘길 경우 맨 왼쪽 칸으로 숫자를 옮긴다. 이와 마찬가지 방법으로 k-(n-1)/2=T((n+1)/2,1) 부터 k+(n-1)/2 = T((n+1)/2, n)까지 채운다.

그 다음에 k-(n-1)/2+1=T((n-1)/2,n)은 k-(n-1)/2=T((n+1)/2,1)의 1칸 오른쪽/1칸 아래에, k+(n+1)/2=T((n+3)/2, 1)은 k+(n-1)/2 = T((n+1)/2,n)의 1칸 왼쪽/1칸 위에 적는다. 역시 아래의 그림을 참조하자. 이와 같은 방법으로 T(a,k), k=1,...n이 완성되었을 때 T(a,k)의 1칸 왼쪽/1칸 위에 T(a+1, k+1) (k=n이면 k+1은 1로 간주), T(a,k)의 1칸 오른쪽/1칸 아래에 T(a-1,k-1) (k=1이면 k-1=n으로 간주)가 적힌다.

이러한 방법으로 1=T(1,1)부터 n²=T(n,n)까지 채울 수 있다. 여기서 위의 그림처럼 T(a,b)와 T(a,b+1)의 간격이 가로/세로 모두 n과 서로소이고, T(a,n)에서 T(a+1,1)의 이동간격도 가로/세로가 모두 n과 서로소이면서 두 개의 이동간격이 서로 겹치지 않을 때 마방진이 형성된다. 왜냐하면 각 마방진에서 T^-1(n)∈[n]×[n]을 고려하면 격자점의 집합 {(k,l)}은 같은 행/같은 열에서 k값과 l값이 일치할 수 없기 때문이다. 즉 i 또는 j 중 하나가 고정되고 나머지 변수로 움직인다고 가정할 때 집합
{T^-1(X_ij)=(a_i1,b_ij)}
는 h≠i일 때 a_ij≠a_hj, b_ij≠b_hj, k≠j일 때 a_ij≠a_ik, b_ij≠b_ik임을 통해 각각 [n]*[n]상에서 같은 행/열에 2개 이상의 원소가 존재하지 않는 n개의 격자점의 배열이 된다.

특히 위의 방식을 이용해 유도된 마방진은 n=6a+3 형태가 아닐 때(즉 6a±1 형태일 때) 완전대각방진(Panmagic Square)을 이룬다. 가로, 세로 대각선 모두 5×5 예제와 7×7 예제를 살펴보자.

5×5 완전대각방진

25	3	6	14	17
11	19	22	5	8
2	10	13	16	24
18	21	4	7	15
9	12	20	23	1

7×7 완전대각방진

49	23	4	34	8	38	19
11	41	15	45	26	7	30
22	3	33	14	37	18	48
40	21	44	25	6	29	10
2	32	13	36	17	47	28
20	43	24	5	35	9	39
31	12	42	16	46	27	1

4n형태

추가예정.

4n+2 짝수 마방진

당연히 n=0일 때에는 마방진이 생기지 않는다. 위의 두 경우보다는 다소 복잡하게 나온다.

마방진의 크로네커 곱

두 마방진 A, B의 크로네커 곱(Kroneker Product)도 마방진이 된다. 이를 이용해서 복합 방진을 가장 간단하게 만들 수 있다. 특히 A, B가 완전마방진(Panmagic Square)이 되면 크로네커 곱도 완전마방진이 된다.

라틴방진

라틴방진(Latin Square)은 nXn 정사각행렬 중 1부터 n까지 원소가 n개씩 배열되어 있고, 각 행과 열에는 1부터 n까지 하나씩 들어가 있는 방진을 의미한다.

또한 두 라틴방진의 행렬 A=(a_ij), B=(b_ij)에 대해서 a_ij=k인 i,j를 모을 때 {b_ij}가 1부터 n까지 하나씩 들어가 있게 되는 경우 두 라틴방진 A와 B는 직교(orthogonal)한다고 말한다. 서로 직교하는 n차 라틴방진 A, B에 대해서 좌표행렬 ((a_ij,b_ij)는 (1,1)부터 (n,n)까지의 격자점 n²개가 하나씩 모인 형태가 되고, 다라서 행렬 ((n-1)a_ij+b_ij)은 1부터 n²까지의 원소로 구성된 준마방진이 된다.

예시

• 서로 직교하는 3x3 라틴방진과 3x3 마방진

1	3	2	×	2	3	1	→	2	9	4
3	2	1		1	2	3		7	5	3
2	1	3		3	1	2		6	1	8

사토르 방진

• 출처: 위키백과:사토르 마방진

사토르 마방진은 가로로 읽으나 세로로 읽으나 똑같이 읽히는 다음절의 다어절로 이루어진 문장이다. 여기서 세로로 읽는다는 것은 왼쪽에서부터 읽는 것이며, 각 어절 당 음절 수는 어절 수만큼 딱 맞아야 한다.

또한 사토르 방진의 문장 SATOR AREPO TENET OPERA ROTAS는 뒤에서부터 읽어도 같은 말이 되기에 회문이 된다. 여담으로 이 문장의 해석은 아래와 같다.

• SATOR (serene - "씨를 뿌리다"에서 유래)- 씨 뿌리는 사람
• AREPO - 라틴어에는 해당 단어가 없으며, 고유명사처럼 사용한다.
• TENET (tenere-"붙잡다"에서 유래) 붙잡다
• OPERA - 일, 작업
• ROTAS - (명사 rota에서 유래) 바퀴(복수형)

즉 "씨 뿌리는 사람 Arepo가 작업용 바퀴들를 가지고 있다"(Arepo the sower holds work wheels.)를 의미한다.

예시

라 팔 아 팔 렸 니 아 니 오

전 지 현 지 석 진 현 진 영

한국어에서는 ABC BDE CEF 패턴이 되면 사토르 마방진이 되는데, 대표적인 예로 ‘개똥아 똥쌌니 아니오’, ‘곰돌아 돌았니 아니오’, ‘전지현 지석진 현진영’등이 있다.

변형된 형태

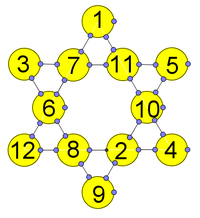
정사각형 대신에 정육각형 배열로 구성된 Magic Hexagon이 있다.

또한 최석정의 산학원본(算學原本)에서는 마방진의 변형된 형태가 나온다. 대표적으로 육각형 형태로 숫자가 배열되어 있고, 각 육각형의 숫자들의 합이 일정한 지수귀문도, 십자가 모양의 사각형 모양인 낙서사구도, 방사형 형태의 중상용구도, 마방진+8각형 숫자 배열인 낙서구구도, 팔각형의 합을 구하는 후책용구도가 있다.

별 모양

각 변의 합이 26인 육각 별 모양(Magic Hexagram) 배열은 다음과 같다.

좀 더 일반적으로, 육각별, 칠각별, 팔각별 배열도 존재한다. 단 오각별 배열은 존재하지 않는다.

Magic hexagram M = 26	Magic heptagram M = 30	Magic octagram M = 34

산학원본에 나타난 형태

지수귀문도

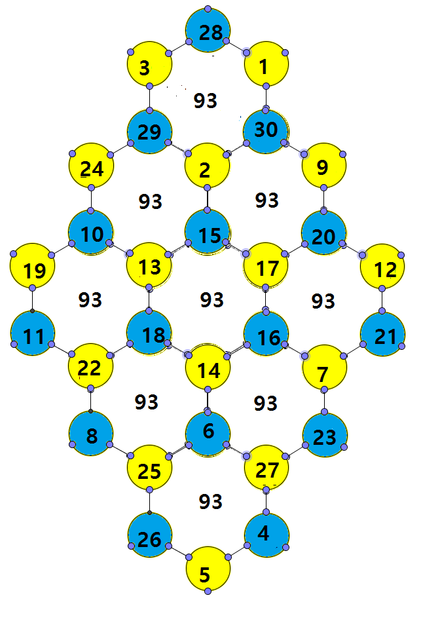
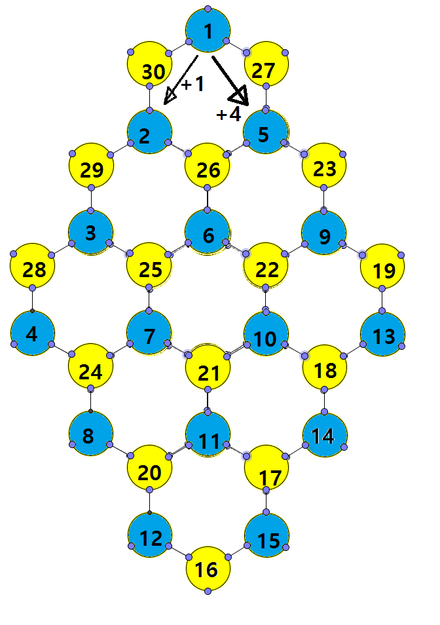
지수귀문도(地數龜文圖)는 벌집 모양으로 배열된 숫자들이 1부터 1개씩 커지면서 각 육각형의 여섯 꼭지점의 숫자의 합이 모두 일치하는 형태를 말한다. 최석정의 구수략(九數略)에서는 칸이 9개, 꼭지점이 30개인 다음과 같은 지수귀문도가 나온다.

지수귀문도는 육각형의 꼭지점의 합을 계산할 때 모두 합해서 한 번만 합하는 꼭지점, 두 번 합하는 꼭지점, 그리고 세 번 합하는 꼭지점이 존재한다. 이러한 특성 때문에 지수귀문도의 육각형의 원소의 합은 다르게 나올 수 있다.

지수귀문도를 가장 쉽게 푸는 방법을 소개한다. 이게 지수귀문도의 배열을 만족한다는 것은 파란색 꼭지점의 경우 육각형이 왼쪽 아래 혹은 오른쪽 아래로 내려갈 때 각각 +1씩/+4씩 커지고, 노란색 꼭지점의 경우 육각형이 왼쪽 아래/오른쪽 아래로 내려갈 때마다 각각 -1씩/-4씩 작아지는 것으로 쉽게 보일 수 있다. 참고로 이 경우는 육각형의 꼭지점의 원소의 합이 위와는 다르게 나오는 것을 참조하자. 육각형이 단지 아래의 배열일 뿐만 아니라 정사각 배열일 때 모두 풀 수 있다. 또한 시작점을 아래 그림의 맨 위쪽 노란색 점으로 하거나 꼭지점 채우는 규칙을 위/아래/위/아래 형식으로 변형하는 방법으로도 다른 지수귀문도 배열을 만들 수 있다.

1. 우선 맨 위의 꼭지점을 하나의 색깔로 칠한 뒤(파란색) 인접한 꼭지점의 색은 다른 색깔(노란색)로 칠한다. 위의 그림처럼 인접한 꼭지점은 서로 다른 색깔로 칠해질 것이다.
2. 그 다음 맨 위의 꼭지점에 숫자 1을 쓴다.
3. 위의 그림처럼 왼쪽 아래의 육각형의 꼭지점에는 2를 쓴다. 2는 왼쪽 아래 육각형의 맨 위 꼭지점과 동일하다.
4. 위의 그림처럼 2의 왼쪽 아래에 3, 3의 왼쪽 아래에 4를 쓴다.
5. 이제 1과 같은 육각형의 오른쪽 아래에 5를 쓴다.
6. 3~4번과 마찬가지로 왼쪽 아래로 내려가면서 6~8을 채운다.
7. 마찬가지로 9~12, 13~15까지 채울 수 있다.
8. 이제는 맨 아래에 노란색 꼭지점에 16을 적는다.
9. 1↙2와는 반대로 노란색 꼭지점에서 ↗방향으로 올라가면서 17, 18, 19를 채운다.
10. 16에서 왼쪽 위 방향의 노란색 꼭지점에 20을 채운 뒤 (9)번처럼 ↗방향으로 21,22,23을 채운다. 마찬가지로 20의 왼쪽 위 방향의 노란색 꼭지점 24를 채운 뒤 마찬가지로 25~27, 28을 채운 뒤 마찬가지로 29 30을 채울 수 있다.

관련 문서

• 레크리에이션/수학

각주

이 문서에는 언어 오류판 위키백과의 740717847 문서 일부 판을 번역한 내용이 포함되어 있습니다.