Ramsey's theorem
개요
자연수 r, s가 주어졌다고 하자. 어떤 충분히 큰 완전그래프의 변을 빨간색과 파란색으로 색칠한다고 할 때, 꼭짓점의 갯수가 r이고 변의 색깔이 모두 빨간색이거나, 꼭짓점의 갯수가 s이고 변의 색깔이 모두 파란색인 완전그래프를 포함한다. 이 때, 이 조건을 만족하는 최소의 꼭짓점의 개수를 [math]\displaystyle{ R(r,s) }[/math]로 표시한다.
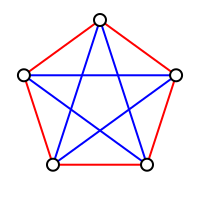
잘 알려진 예는 [math]\displaystyle{ R(3,3) = 6 }[/math]. 실생활에 적용하면, 6명의 사람이 있을 때, 서로 아는 3명이나 서로 모르는 3명이 존재한다. 크기가 5일 때에는 변의 색이 모두 같고 크기가 3인 완전그래프를 포함하지 않는다. 다음에 나올 증명에 의해[math]\displaystyle{ R(3,3) \leq 6 }[/math]을 알 수 있어, [math]\displaystyle{ R(3,3) = 6 }[/math]임을 알 수 있다.
증명
귀납법을 사용한다. 대신에 두 변수에 대해 사용할 것이다.
- [math]\displaystyle{ R(r,2) = r, R(2,s)=s }[/math]
- 꼭짓점이 2개이면, 변은 1개다. 즉, 하나라도 다른 색이 있으면 꼭짓점의 개수가 2인 완전그래프를 포함하게 된다. 그것이 아니라면 모든 변의 색이 같아진다.
- 이제, [math]\displaystyle{ R(r-1,s), R(r,s-1) }[/math]이 존재한다고 가정하자.
- 한 꼭지점을 고른다. 그리고 고른 꼭지점과 연결된 변이 빨간색인 집합 A와 파란색인 집합 B으로 나눌 수 있다.
- 만약 집합 A의 원소의 개수가 [math]\displaystyle{ R(r-1,s) }[/math]이라면
- 변이 모두 빨간색이고 크기가 r-1인 완전그래프가 있다면, 처음 고른 꼭지점을 추가해 크기가 r인 완전그래프를 얻을 수 있다.
- 변이 모두 파란색이고 크기가 s인 완전그래프가 있다면 이걸로 끝.
- 만약 집합 B의 원소의 개수가 [math]\displaystyle{ R(r,s-1) }[/math]이라면
- 변이 모두 빨간색이고 크기가 r인 완전그래프가 있다면 끝.
- 변이 모두 파란색이고 크기가 s-1인 완전그래프가 있다면, 처음 고른 꼭지점을 추가해 크기가 s인 완전그래프를 얻을 수 있다.
- 만약 집합 A의 원소의 개수가 [math]\displaystyle{ R(r-1,s) }[/math]이라면
- 그러면 이제 두 개로 나눴을 때 저 두 조건중 하나를 만족하려면 최소한 꼭지점의 개수가 고를 꼭지점 포함해서 [math]\displaystyle{ R(r-1,s) + R(r,s-1) }[/math]여야 한다. 이건 비둘기집의 원리에 의해 유도할 수 있다.
- [math]\displaystyle{ R(r-1,s) + R(r,s-1) }[/math]개의 꼭지점이 있으면 r, s에 대해 램지의 정리를 만족하도록 할 수 있다. 상계값을 찾은 것이다. 그러므로 [math]\displaystyle{ R(r,s) \leq R(r-1,s) + R(r,s-1) }[/math]이다. 정확한 값은 알 수 없지만 존재한다는 것은 알 수 있다.
- 한 꼭지점을 고른다. 그리고 고른 꼭지점과 연결된 변이 빨간색인 집합 A와 파란색인 집합 B으로 나눌 수 있다.
일반화
꼭 색을 두가지만 칠하라는 법은 없다. 여러 가지 색에 대해서도 똑같은 논리를 전개할 수 있다. 표현은 [math]\displaystyle{ R(r,s,t,...) }[/math]로 표시한다.