라플라스 변환

정의

[math]\displaystyle{ 0\le t\lt \infty }[/math]에서 정의된 함수 f에 대해,

[math]\displaystyle{ F(s)=\mathcal{L}(f(t))=\int_0^{\infty}f(t)e^{-st}dt\quad(s\in \mathbb{C}) }[/math]

를 f(t)의 라플라스 변환(Laplace transform), 또는 단방향 라플라스 변환(Unilateral laplace transform)이라 한다. 그러면 "양방향"도 있을 것 같은데, 실제로 쓰고 있다.
함수가 [math]\displaystyle{ -\infty\lt t\lt \infty }[/math]에서 정의되어 있을 때,

[math]\displaystyle{ \mathcal{B}(f(t))=\int_{-\infty}^{\infty}e^{-st}f(t)dt }[/math]

를 양방향 라플라스 변환(Bilateral laplace transform)이라 한다. 이 문서에서는 단방향 라플라스 변환에 대해서만 다룬다.

존재성

라플라스 변환이 언제나 존재하는 것은 아니다. 예를 들어 [math]\displaystyle{ f(t)=e^{t^2} }[/math]라면

[math]\displaystyle{ F(s)=\int_0^{\infty}e^{t^2-st}dt=\infty }[/math]

이므로 f의 라플라스 변환은 존재하지 않는다. 함수 f에 대해 양수 M, t₀와 실수 α가 존재하여 임의의 t≥t₀에 대해

[math]\displaystyle{ |f(t)|\le M e^{\alpha t} }[/math]

를 만족하면 f는 지수적 차수(exponential order) α를 가진다고 한다. 만약 f가 [math]\displaystyle{ [0,\infty) }[/math]에서 조각적 연속이고 지수적 차수 α를 가진다면, f의 라플라스 변환은 [math]\displaystyle{ \operatorname{Re}s \gt \alpha }[/math]에서 존재하고 절대수렴한다. 단, 역은 성립하지 않는다. 예를 들어 [math]\displaystyle{ f(t)=\ln t }[/math]는 [math]\displaystyle{ [0,\infty) }[/math]에서 조각적 연속이 아니지만

[math]\displaystyle{ \mathcal{L}(\ln t)=-\frac{\ln s +\gamma}{s} }[/math]

이다. 이때 γ는 오일러-마스케로니 상수다.

유일성

어떤 라플라스 변환에 대응되는 함수는 일반적으로 유일하지 않다. 예를 들어, 함수 f, g를 다음과 같이 정의하자.

[math]\displaystyle{ f(t)=e^{-t} }[/math]

[math]\displaystyle{ g(t)=\begin{cases} e^{-t} & (0\le x \lt 1, 1\lt x\lt \infty)\\ 1 & (x= 1) \end{cases} }[/math]

그러면 [math]\displaystyle{ F(s)=G(s)=\dfrac{1}{s+1} }[/math]이다. 따라서 [math]\displaystyle{ H(s)=\dfrac{1}{s+1} }[/math]인 함수 h는 유일하지 않다. 이 결과는 라플라스 변환을 기껏 정의해놓고서 못 쓰는 건 아닌가 하는 불안을 불러일으킨다. 다행히 역라플라스 변환으로 (조각적) 연속함수를 찾는다면 그 연속함수는 유일하기 대문에 걱정하지 않아도 된다. 다시 말하면, 정의역이 [math]\displaystyle{ [0,\infty) }[/math]인 연속함수 f,g에 대해 [math]\displaystyle{ F(s)=G(s) }[/math]이면 f=g이다. 더 나아가, 정의역이 [math]\displaystyle{ [0,\infty) }[/math]인 조각적 연속함수 f,g에 대해 [math]\displaystyle{ F(s)=G(s) }[/math]이면 불연속인 점을 제외했을 때 f=g이다.

역라플라스 변환

[math]\displaystyle{ F(s)=\mathcal{L}(f(t)) }[/math]이면 f(t)를 F(s)의 역라플라스 변환(Inverse laplace transformation)이라고 한다. 만약 f가 [math]\displaystyle{ [0,\infty) }[/math]에서 연속이고 t<0일 때 f(t)=0이며, 지수적 차수 α를 가지고 f' 가 [math]\displaystyle{ [0,\infty) }[/math]에서 조각적 연속이면, 역라플라스 변환은 다음 공식으로 나타낼 수 있다.

[math]\displaystyle{ f(t)=\lim_{y\to\infty}\frac{1}{2\pi i}\int_{x-iy}^{x+iy}e^{ts}F(s)ds }[/math] (푸리에-멜린 반전공식)

그런데 이 공식을 잘 쓰려면 유수 정리 같은 복소함수론의 정리를 잘 이용해야 하므로 복소함수론을 배우지 않았으면 이 공식 대신 라플라스 변환표에서 변환에 맞는 함수를 찾아서 쓴다. 적분을 직접 하고 싶다? 직접 해보자. 어떤 연속함수 f의 라플라스 변환이 다음과 같이 주어졌다고 하자.

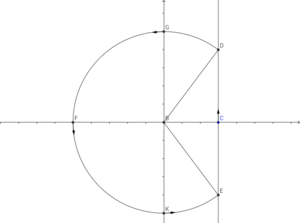
[math]\displaystyle{ F(s)=\frac{2as}{(s^2+a^2)^2} }[/math]

그림은 복소함수의 경로적분 설정. 푸리에-멜린 반전공식 하나를 이용하기 위해 적분경로를 설정하고 유수 정리를 활용해야 한다. 학부 수준에서 쓸 만한 역변환은 표에 거의 다 나와 있으므로, 차라리 그걸 외우자.

그러면 [math]\displaystyle{ F(s) }[/math]는 [math]\displaystyle{ s=\pm ai }[/math]에서 이차극점을 가진다. 이때 그림과 같이 복소평면 위에 점 (x,0)을 지나고 허수축과 평행인 직선 ED와, 원점을 중심으로 하고 경로가 DGFKE인 부분원 [math]\displaystyle{ C_R }[/math]을 생각하자. 이때 [math]\displaystyle{ R^2=x^2+y^2 }[/math]이다. [math]\displaystyle{ R\gt a }[/math]이 되도록 충분한 R을 설정할 수 있고, 이때 극점 [math]\displaystyle{ \pm ai }[/math]는 닫힌 경로 EDGFKE의 내부에 속한다. 이때 이 경로를 [math]\displaystyle{ \Gamma }[/math]라고 하자. 그러면

[math]\displaystyle{ \int_{\Gamma}e^{ts}F(s)ds=\int_{ED}e^{ts}F(s)ds+\int_{C_R}e^{ts}F(s)ds }[/math]

이다. 이때

[math]\displaystyle{ \lim_{R\to\infty}\int_{C_R}e^{ts}F(s)ds=0 }[/math]

이고 유수 정리에 의해

[math]\displaystyle{ \int_{\Gamma}e^{ts}F(s)ds=2\pi i(\operatorname{Res}(ai)+\operatorname{Res}(-ai)) }[/math]

이다. 계산을 열심히 하면

[math]\displaystyle{ \operatorname{Res}(ai)=-\frac{1}{2}ite^{iat},\quad \operatorname{Res}(-ai)=\frac{1}{2}ite^{-iat} }[/math]

이므로

[math]\displaystyle{ \begin{align}\int_{\Gamma}e^{ts}F(s)ds&=2\pi i\left(-\frac{1}{2}ite^{iat}+\frac{1}{2}ite^{-iat} \right)\\ &=2\pi i t\left(\frac{e^{iat}-e^{-iat}}{2i}\right)\\ &=2\pi i t\sin at \end{align} }[/math]

이다. 이 식을 푸리에-멜린 반전공식에 대입하면

[math]\displaystyle{ f(t)=t\sin at }[/math]

를 얻는다. 그런데 이거 라플라스 변환표에 기본적으로 나와있는 것이므로, 꼭 필요한 때가 아니라면 이 문서처럼 쓸데없이 길게 적분하지 말고 변환표 외우자.

성질

[math]\displaystyle{ \mathcal{L}(f_1(t))=F_1(s),\mathcal{L}(f_2(t))=F_2(s) }[/math]

원함수	변환	수렴영역
[math]\displaystyle{ \mathcal{L}(c_1 f_1(t)+c_2f_2(t)) }[/math]	[math]\displaystyle{ c_1F_1(s)+c_2F_2(s) }[/math]
[math]\displaystyle{ \mathcal{L}(f^{(n)}(t)) }[/math]	[math]\displaystyle{ s^n\mathcal{L}(f(t))-s^{n-1}f(0)-\cdots-f^{(n-1)}(0) }[/math]
[math]\displaystyle{ \mathcal{L}(t^n f(t)) }[/math]	[math]\displaystyle{ (-1)^n F^{(n)}(s) }[/math]
[math]\displaystyle{ \mathcal{L}\left(\int_0^t f(u)du\right) }[/math]	[math]\displaystyle{ \frac{F(s)}{s} }[/math]
[math]\displaystyle{ f(t+T)=f(t) }[/math]	[math]\displaystyle{ \dfrac{\int_0^T e^{-st}f(t)dt}{1-e^{sT}} }[/math]
[math]\displaystyle{ (f * g)(t) }[/math]	[math]\displaystyle{ F(s)G(s) }[/math]
참고사항. [math]\displaystyle{ (f * g)(t)=\int_0^{\tau} f(\tau)g(t - \tau)d\tau }[/math]는 합성곱.

라플라스 변환표

공업수학에서 필수적으로 이 관련 표가 나온다. 적어도 이 표는 죄다 외워주는게 시험보기 편하다. 잘 못외우면 [math]\displaystyle{ e^{t} }[/math]의 변환이 [math]\displaystyle{ \frac1s }[/math]이라는 것을 외우고, 이걸 더하고 빼고 해서 삼각함수 쪽은 다 직접 유도할 수 있긴 하다. 하지만 역시 외우는게 편하다.

이걸 어떻게 다 외워? 살려줘~~

[math]\displaystyle{ f(t) }[/math]	[math]\displaystyle{ \mathcal{L}(f) }[/math]	수렴영역
1	[math]\displaystyle{ \frac{1}{s} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ t^p }[/math] (단, p>-1)	[math]\displaystyle{ \frac{\Gamma(p+1)}{s^{p+1}} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ \sin(at) }[/math]	[math]\displaystyle{ \frac{a}{s^2+a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ \cos(at) }[/math]	[math]\displaystyle{ \frac{s}{s^2+a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ t\sin(at) }[/math]	[math]\displaystyle{ \frac{2as}{(s^2+a^2)^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ t\cos(at) }[/math]	[math]\displaystyle{ \frac{s^2-a^2}{(s^2+a^2)^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt 0 }[/math]
[math]\displaystyle{ \sinh(at) }[/math]	[math]\displaystyle{ \frac{a}{s^2-a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt |a| }[/math]
[math]\displaystyle{ \cosh(at) }[/math]	[math]\displaystyle{ \frac{s}{s^2-a^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt |a| }[/math]
[math]\displaystyle{ e^{at} }[/math]	[math]\displaystyle{ \frac{1}{s-a} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ e^{at}\sin(bt) }[/math]	[math]\displaystyle{ \frac{b}{(s-a)^2+b^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ e^{at}\cos(bt) }[/math]	[math]\displaystyle{ \frac{s-a}{(s-a)^2+b^2} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ t^n e^{at} }[/math] (단, n은 자연수)	[math]\displaystyle{ \frac{n!}{(s-a)^{n+1}} }[/math]	[math]\displaystyle{ \operatorname{Re} s\gt a }[/math]
[math]\displaystyle{ H_c(t) }[/math] (단, c>0)	[math]\displaystyle{ \frac{e^{-cs}}{s} }[/math]
[math]\displaystyle{ \delta_c(t) }[/math] (단, c>0)	[math]\displaystyle{ e^{-cs} }[/math]
참고사항. [math]\displaystyle{ \Gamma(t) }[/math]는 감마함수. [math]\displaystyle{ H_c(t) }[/math]는 헤비사이드 함수. [math]\displaystyle{ \delta_c(t) }[/math]는 디랙 델타 함수.

이걸 어떻게 다 외워? 살려줘~~

다른 변환과의 관계

푸리에 변환

푸리에 변환은

[math]\displaystyle{ \mathcal{F}(f(t))=\hat{f}(\xi)=\int_{-\infty}^{\infty}f(t)e^{-2\pi i t \xi}dt\quad(\xi\in\mathbb{R}) }[/math]

로 주어지는데, 붕괴인자(Decaying factor) [math]\displaystyle{ e^{-\sigma t}\;(\sigma\in\mathbb{R}) }[/math]를 곱하면 주어진 변환은

[math]\displaystyle{ \int_{-\infty}^{\infty}f(t)e^{-\sigma t-2\pi i t \xi}dt\quad(\xi\in\mathbb{R}) }[/math]

이고 [math]\displaystyle{ s=\sigma+2\pi i \xi }[/math]로 두면

[math]\displaystyle{ \int_{-\infty}^{\infty}f(t)e^{-st}dt }[/math]

이고, 이 식은 양방향 라플라스 변환과 동일하다. t<0일 때 [math]\displaystyle{ f(t)=0 }[/math]라고 하면,

[math]\displaystyle{ \int_0^{\infty}f(t)e^{-st}dt }[/math]

이 되므로 라플라스 변환이 된다. 따라서 다음 식이 성립한다.

[math]\displaystyle{ \mathcal{F}(f(t)e^{-\sigma t})=\mathcal{L}(f(t)) }[/math]

활용

미분방정식의 풀이

미분방정식 교재 여럿이 이계 미분방정식을 푸는 방법으로 라플라스 변환을 도입한다. 미분방정식

[math]\displaystyle{ \frac{d^2x}{dt^2}+2\beta \frac{dx}{dt}+w_0^2 x = 0 }[/math]

이 주어졌다고 하자. 이때 양변의 라플라스 변환은

[math]\displaystyle{ (s^2F(s)-sf(0)-f'(0))+2\beta(sF(s)-f(0))+w_0^2F(s)=0 }[/math]

이고, 식을 F(s)에 대해 나타내면

[math]\displaystyle{ F(s)=\dfrac{(s+2\beta)f(0)+f'(0)}{s^2+2\beta s +w_0^2}=\frac{(s+\beta)f(0)}{s^2+2\beta s +w_0^2}+\frac{\beta f(0)+f'(0)}{s^2+2\beta s +w_0^2} }[/math]

이다. [math]\displaystyle{ F_1(s),F_2(s) }[/math]를 다음과 같이 정의하자.

[math]\displaystyle{ F_1(s)=\frac{(s+\beta)f(0)}{s^2+2\beta s +w_0^2} }[/math]

[math]\displaystyle{ F_2(s)=\frac{\beta f(0)+f'(0)}{s^2+2\beta s +w_0^2} }[/math]

[math]\displaystyle{ w_0^2\gt \beta^2 }[/math]라고 가정하자. 그러면

[math]\displaystyle{ F_1(s)=f(0)\frac{s+\beta}{(s+\beta)^2+(\sqrt{w_0^2-\beta^2})^2}=f(0)\mathcal{L}(e^{-\beta t}\cos(\sqrt{w_0^2-\beta^2}t)) }[/math]

[math]\displaystyle{ F_2(s)=\frac{\beta f(0)+f'(0)}{\sqrt{w_0^2-\beta^2}}\frac{\sqrt{w_0^2-\beta^2}}{(s+\beta)^2+(\sqrt{w_0^2-\beta^2})^2}=\frac{\beta f(0)+f'(0)}{\sqrt{w_0^2-\beta^2}}\mathcal{L}(e^{-\beta t}\sin(\sqrt{w_0^2-\beta^2}t)) }[/math]

따라서

[math]\displaystyle{ x(t)=f(0)e^{-\beta t}\cos(\sqrt{w_0^2-\beta^2}t)+\frac{\beta f(0)+f'(0)}{\sqrt{w_0^2-\beta^2}}\cdot e^{-\beta t}\sin(\sqrt{w_0^2-\beta^2}t) }[/math]

를 얻는다.어때요, 정말 쉽죠?

이외에 편미분방정식을 푸는 데도 라플라스 변환이 유용하게 쓰일 수 있다.

[math]\displaystyle{ y=y(x,t)\;(t\gt 0) }[/math]

이고 t를 시간 변수라 하면, y에 대한 라플라스 변환 [math]\displaystyle{ Y(x,s) }[/math]는

[math]\displaystyle{ U(x,s)=\int_0^{\infty}e^{-st}y(x,t)dt }[/math]

이다.

편미분방정식

[math]\displaystyle{ \frac{\partial y}{\partial x}+\frac{1}{x}\frac{\partial y}{\partial t}=t,\quad x\gt 0,t\gt 0. }[/math]

[math]\displaystyle{ y(x,0^+)=x,\quad y(0,t)=t }[/math]

를 라플라스 변환을 이용해 풀어보자. 양변에 라플라스 변환을 적용하면

[math]\displaystyle{ \mathcal{L}\left(\frac{dy}{dx}\right)=\frac{dU(x,s)}{dx},\quad\mathcal{L}\left(\frac{dy}{dt}\right)=sU(x,s)-u(x,0^+) }[/math]

이므로

[math]\displaystyle{ \frac{dU(x,s)}{dx}+\frac{1}{x}(sU(x,s)-u(x,0^+))=\frac{1}{s^2} }[/math]

이고 정리하면

[math]\displaystyle{ \frac{dU(x,s)}{dx}+\frac{s}{x}U(x,s)=1+\frac{1}{s^2} }[/math]

이다. 그러면

[math]\displaystyle{ \frac{d}{dx}(x^s U(x,s))=x^s\left(1+\frac{1}{s^2}\right) }[/math]

이므로

[math]\displaystyle{ U(x,s)=\left(1+\frac{1}{s^2}\right)\frac{1}{s+1}x+Cx^{-s} }[/math]

이다. [math]\displaystyle{ s\to 0^+ }[/math]이면 [math]\displaystyle{ x+C=x }[/math]이므로 [math]\displaystyle{ C=0 }[/math]를 얻는다. 따라서

[math]\displaystyle{ U(x,s)=\left(1+\frac{1}{s^2}\right)\frac{1}{s+1}x }[/math]

이므로 열심히 조작하면

[math]\displaystyle{ U(x,s)=\left(\frac{2}{s+1}-\frac{1}{s}+\frac{1}{s^2}\right)x }[/math]

이다. 따라서

[math]\displaystyle{ y(x,t)=(2e^{-t}-1+t)x }[/math]

을 얻는다.

이상적분의 계산

라플라스 변환을 이용하면 부정적분이 초등함수로 나타나지 않는 함수의 이상적분을 계산할 수 있다. 이상적분

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-x}-e^{-2x}}{x}dx }[/math]

를 계산해보자. [math]\displaystyle{ f(x)=\dfrac{e^{-x}-e^{-2x}}{x} }[/math]라 하면 [math]\displaystyle{ xf(x)=e^{-x}-e^{-2x} }[/math]이다. f의 라플라스 변환을 F(s)라 하면 F(s)는 [math]\displaystyle{ s\gt -1 }[/math]일 때 존재하고

[math]\displaystyle{ - \frac{dF(s)}{ds}=\frac{1}{s+1}-\frac{1}{s+2} }[/math]

이다. 정리하면

[math]\displaystyle{ F(s)=\ln(s+2)-\ln(s+1) }[/math]

을 얻는다. 따라서

[math]\displaystyle{ \ln(s+2)-\ln(s+1)=F(s)=\int_0^{\infty}e^{-sx}\frac{e^{-x}-e^{-2x}}{x}dx }[/math]

이며, [math]\displaystyle{ s=0 }[/math]을 대입하면

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-x}-e^{-2x}}{x}dx=\ln 2 }[/math]

를 얻는다. 일반적으로

[math]\displaystyle{ \mathcal{L}\left(\frac{f(t)}{t}\right)=\int_s^{\infty}F(u)du }[/math]

이므로 라플라스 변환의 정의에 의해

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-st}f(t)}{t}dt=\int_s^{\infty}F(u)du }[/math]

이고, 수렴영역이 [math]\displaystyle{ s\gt a }[/math]이면 [math]\displaystyle{ s\to a+ }[/math]일 때

[math]\displaystyle{ \int_0^{\infty}\frac{e^{-at}f(t)}{t}dt=\int_a^{\infty}F(u)du }[/math]

를 얻는다.

점화식의 일반항 계산

라플라스 변환을 이용해 점화식으로 주어진 수열의 일반항을 구할 수 있다.

[math]\displaystyle{ \mathcal{L}(a^{\lfloor t \rfloor})=\frac{1-e^{-s}}{s(1-ae^{-s})} }[/math]

임을 이용하여 점화식

[math]\displaystyle{ a_{n+2}-a_{n+1}-a_n=0,\;a_0=0,\;a_1=1 }[/math]

으로 주어진 피보나치 수열의 일반항을 구해보자. 함수 f를

[math]\displaystyle{ f(t)=a_n\quad(n\le t\lt n+1) }[/math]

로 정의하자. 그러면 주어진 점화식은

[math]\displaystyle{ f(t+2)-f(t+1)-f(t)=0 }[/math]

으로 나타낼 수 있다. 이때,

[math]\displaystyle{ \begin{align} \mathcal{L}(f(t+2))&=\int_0^{\infty}e^{-st}f(t+2)dt\\ &=\int_2^{\infty}e^{-s(u-2)}f(u)du\\ &=\int_0^{\infty}e^{-s(u-2)}f(u)du-\int_0^2e^{-s(u-2)}f(u)du\\ &=e^{2s}\mathcal{L}(f(t))-e^{2s}\left(\frac{e^{-s}-e^{-2s}}{s}\right)\\ &=e^{2s}\mathcal{L}(f(t))-\frac{e^s-1}{s} \end{align} }[/math]

이고

[math]\displaystyle{ \mathcal{L}(f(t+1))=e^s \mathcal{L}(f(t)) }[/math]

이다. 그러므로

[math]\displaystyle{ \begin{align} \mathcal{L}(f(t))&=\frac{e^s-1}{s(e^{2s}-e^s-1)}\\ &=\frac{e^s-1}{\sqrt{5}s}\left(\frac{1}{e^s-\frac{1+\sqrt{5}}{2}}-\frac{1}{e^s-\frac{1-\sqrt{5}}{2}}\right)\\ &=\frac{1}{\sqrt{5}}\left(\frac{1-e^{-s}}{s(1-\frac{1+\sqrt{5}}{2}e^{-s})}-\frac{1-e^{-s}}{s(1-\frac{1-\sqrt{5}}{2}e^{-s})}\right)\\ &=\frac{1}{\sqrt{5}}\left(\mathcal{L}\left(\left(\frac{1+\sqrt{5}}{2}\right)^{\lfloor t \rfloor}\right)-\mathcal{L}\left(\left(\frac{1-\sqrt{5}}{2}\right)^{\lfloor t \rfloor}\right)\right) \end{align} }[/math]

이므로 [math]\displaystyle{ \bigcup_{m\in\mathbb{N}}(m,m+1) }[/math]에서

[math]\displaystyle{ f(t)=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^{\lfloor t \rfloor}-\left(\frac{1-\sqrt{5}}{2}\right)^{\lfloor t \rfloor}\right) }[/math]

이고, [math]\displaystyle{ t=n+\frac{1}{2} }[/math]을 대입하면

[math]\displaystyle{ a_n=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right) }[/math]

을 얻는다.나는 괄호가 싫어요

같이 보기

• 푸리에 변환